Posted on 2011-04-21 23:36
沙漠中的鱼 阅读(376)
评论(0) 编辑 收藏 所属分类:
Java 、
Java基础
Java 语言支持两种基本的浮点类型： float 和 double ，以及与它们对应的包装类 Float 和 Double 。它们都依据 IEEE 754 标准，该标准为 32 位浮点和 64 位双精度浮点二进制小数定义了二进制标准。
IEEE 754 用科学记数法以底数为 2 的小数来表示浮点数。IEEE 浮点数用 1 位表示数字的符号，用 8 位来表示指数，用 23 位来表示尾数，即小数部分。作为有符号整数的指数可以有正负之分。小数部分用二进制（底数 2）小数来表示，这意味着最高位对应着值 ?(2 -1)，第二位对应着 ?(2 -2)，依此类推。对于双精度浮点数，用 11 位表示指数，52 位表示尾数。IEEE 浮点值的格式如图 1 所示。
图 1. IEEE 754 浮点数的格式
因为用科学记数法可以有多种方式来表示给定数字，所以要规范化浮点数，以便用底数为 2 并且小数点左边为 1 的小数来表示，按照需要调节指数就可以得到所需的数字。所以，例如，数 1.25 可以表示为尾数为 1.01，指数为 0： (-1) 0*1.01 2*2 0
数 10.0 可以表示为尾数为 1.01，指数为 3： (-1) 0*1.01 2*2 3
一个十进制数能否用二进制浮点数精确表示，关键在于小数部分。我们来看一个最简单的小数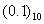
能否精确表示。按照乘以2取整数位的方法，有：
得到一个无限循环的二进制小数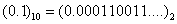
，用有限位无法表示无限循环小数，因此，
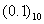无法用IEEE 754浮点数精确表示。从中也可以看到：由于
，
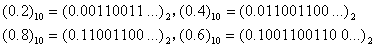这四个数也无法精确表示。同理：
也无法用IEEE 754浮点数精确表示。
在以0.1~0.9结尾的9个小数中，只有0.5可以精确表示：（如）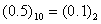
，而其他均无法进行精确转换。