|
游戏算法整理 算法一:A*寻路初探
作者: Patrick Lester
译者:Panic 2005年3月18日
译者序:很久以前就知道了A*算法,但是从未认真读过相关的文章,也没有看过代码,只是脑子里有个模糊的概念。这次决定从头开始,研究一下这个被人推崇备至的简单方法,作为学习人工智能的开始。
这篇文章非常知名,国内应该有不少人翻译过它,我没有查找,觉得翻译本身也是对自身英文水平的锻炼。经过努力,终于完成了文档,也明白的A*算法的原理。毫无疑问,作者用形象的描述,简洁诙谐的语言由浅入深的讲述了这一神奇的算法,相信每个读过的人都会对此有所认识(如果没有,那就是偶的翻译太差了 --b)。
现在是2005年7月19日的版本,应原作者要求,对文中的某些算法细节做了修改。
原文链接:http://www.gamedev.net/reference/articles/article2003.asp
原作者文章链接:http://www.policyalmanac.org/games/aStarTutorial.htm
以下是翻译的正文。
会者不难,A*(念作A星)算法对初学者来说的确有些难度。
这篇文章并不试图对这个话题作权威的陈述。取而代之的是,它只是描述算法的原理,使你可以在进一步的阅读中理解其他相关的资料。
最后,这篇文章没有程序细节。你尽可以用任意的计算机程序语言实现它。如你所愿,我在文章的末尾包含了一个指向例子程序的链接。 压缩包包括C++和Blitz Basic两个语言的版本,如果你只是想看看它的运行效果,里面还包含了可执行文件。
我们正在提高自己。让我们从头开始。。。
序:搜索区域
假设有人想从A点移动到一墙之隔的B点,如下图,绿色的是起点A,红色是终点B,蓝色方块是中间的墙。
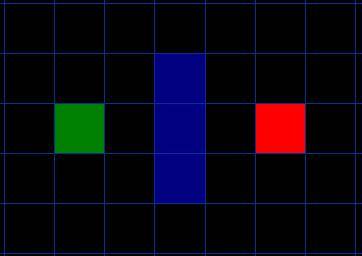
[图1]
你首先注意到,搜索区域被我们划分成了方形网格。像这样,简化搜索区域,是寻路的第一步。这一方法把搜索区域简化成了一个二维数组。数组的每一个元素是网格的一个方块,方块被标记为可通过的和不可通过的。路径被描述为从A到B我们经过的方块的集合。一旦路径被找到,我们的人就从一个方格的中心走向另一个,直到到达目的地。
这些中点被称为“节点”。当你阅读其他的寻路资料时,你将经常会看到人们讨论节点。为什么不把他们描述为方格呢?因为有可能你的路径被分割成其他不是方格的结构。他们完全可以是矩形,六角形,或者其他任意形状。节点能够被放置在形状的任意位置-可以在中心,或者沿着边界,或其他什么地方。我们使用这种系统,无论如何,因为它是最简单的。
开始搜索
正如我们处理上图网格的方法,一旦搜索区域被转化为容易处理的节点,下一步就是去引导一次找到最短路径的搜索。在A*寻路算法中,我们通过从点A开始,检查相邻方格的方式,向外扩展直到找到目标。
我们做如下操作开始搜索:
1,从点A开始,并且把它作为待处理点存入一个“开启列表”。开启列表就像一张购物清单。尽管现在列表里只有一个元素,但以后就会多起来。你的路径可能会通过它包含的方格,也可能不会。基本上,这是一个待检查方格的列表。
2,寻找起点周围所有可到达或者可通过的方格,跳过有墙,水,或其他无法通过地形的方格。也把他们加入开启列表。为所有这些方格保存点A作为“父方格”。当我们想描述路径的时候,父方格的资料是十分重要的。后面会解释它的具体用途。
3,从开启列表中删除点A,把它加入到一个“关闭列表”,列表中保存所有不需要再次检查的方格。
在这一点,你应该形成如图的结构。在图中,暗绿色方格是你起始方格的中心。它被用浅蓝色描边,以表示它被加入到关闭列表中了。所有的相邻格现在都在开启列表中,它们被用浅绿色描边。每个方格都有一个灰色指针反指他们的父方格,也就是开始的方格。

[图2]
接着,我们选择开启列表中的临近方格,大致重复前面的过程,如下。但是,哪个方格是我们要选择的呢?是那个F值最低的。
路径评分
选择路径中经过哪个方格的关键是下面这个等式:
F = G + H
这里:
* G = 从起点A,沿着产生的路径,移动到网格上指定方格的移动耗费。
* H = 从网格上那个方格移动到终点B的预估移动耗费。这经常被称为启发式的,可能会让你有点迷惑。这样叫的原因是因为它只是个猜测。我们没办法事先知道路径的长度,因为路上可能存在各种障碍(墙,水,等等)。虽然本文只提供了一种计算H的方法,但是你可以在网上找到很多其他的方法。
我们的路径是通过反复遍历开启列表并且选择具有最低F值的方格来生成的。文章将对这个过程做更详细的描述。首先,我们更深入的看看如何计算这个方程。
正如上面所说,G表示沿路径从起点到当前点的移动耗费。在这个例子里,我们令水平或者垂直移动的耗费为10,对角线方向耗费为14。我们取这些值是因为沿对角线的距离是沿水平或垂直移动耗费的的根号2(别怕),或者约1.414倍。为了简化,我们用10和14近似。比例基本正确,同时我们避免了求根运算和小数。这不是只因为我们怕麻烦或者不喜欢数学。使用这样的整数对计算机来说也更快捷。你不就就会发现,如果你不使用这些简化方法,寻路会变得很慢。
既然我们在计算沿特定路径通往某个方格的G值,求值的方法就是取它父节点的G值,然后依照它相对父节点是对角线方向或者直角方向(非对角线),分别增加14和10。例子中这个方法的需求会变得更多,因为我们从起点方格以外获取了不止一个方格。
H值可以用不同的方法估算。我们这里使用的方法被称为曼哈顿方法,它计算从当前格到目的格之间水平和垂直的方格的数量总和,忽略对角线方向。然后把结果乘以10。这被成为曼哈顿方法是因为它看起来像计算城市中从一个地方到另外一个地方的街区数,在那里你不能沿对角线方向穿过街区。很重要的一点,我们忽略了一切障碍物。这是对剩余距离的一个估算,而非实际值,这也是这一方法被称为启发式的原因。想知道更多?你可以在这里找到方程和额外的注解。
F的值是G和H的和。第一步搜索的结果可以在下面的图表中看到。F,G和H的评分被写在每个方格里。正如在紧挨起始格右侧的方格所表示的,F被打印在左上角,G在左下角,H则在右下角。
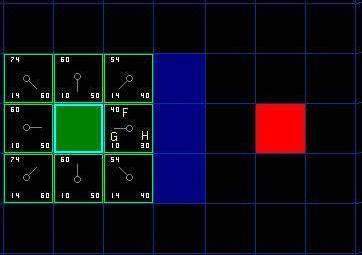
[图3]
现在我们来看看这些方格。写字母的方格里,G = 10。这是因为它只在水平方向偏离起始格一个格距。紧邻起始格的上方,下方和左边的方格的G值都等于10。对角线方向的G值是14。
H值通过求解到红色目标格的曼哈顿距离得到,其中只在水平和垂直方向移动,并且忽略中间的墙。用这种方法,起点右侧紧邻的方格离红色方格有3格距离,H值就是30。这块方格上方的方格有4格距离(记住,只能在水平和垂直方向移动),H值是40。你大致应该知道如何计算其他方格的H值了~。
每个格子的F值,还是简单的由G和H相加得到
继续搜索
为了继续搜索,我们简单的从开启列表中选择F值最低的方格。然后,对选中的方格做如下处理:
4,把它从开启列表中删除,然后添加到关闭列表中。
5,检查所有相邻格子。跳过那些已经在关闭列表中的或者不可通过的(有墙,水的地形,或者其他无法通过的地形),把他们添加进开启列表,如果他们还不在里面的话。把选中的方格作为新的方格的父节点。
6,如果某个相邻格已经在开启列表里了,检查现在的这条路径是否更好。换句话说,检查如果我们用新的路径到达它的话,G值是否会更低一些。如果不是,那就什么都不做。
另一方面,如果新的G值更低,那就把相邻方格的父节点改为目前选中的方格(在上面的图表中,把箭头的方向改为指向这个方格)。最后,重新计算F和G的值。如果这看起来不够清晰,你可以看下面的图示。
好了,让我们看看它是怎么运作的。我们最初的9格方格中,在起点被切换到关闭列表中后,还剩8格留在开启列表中。这里面,F值最低的那个是起始格右侧紧邻的格子,它的F值是40。因此我们选择这一格作为下一个要处理的方格。在紧随的图中,它被用蓝色突出显示。
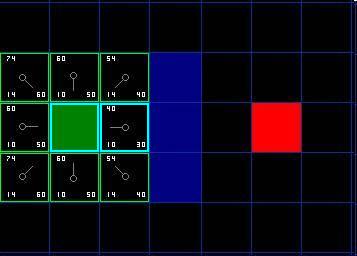
[图4]
首先,我们把它从开启列表中取出,放入关闭列表(这就是他被蓝色突出显示的原因)。然后我们检查相邻的格子。哦,右侧的格子是墙,所以我们略过。左侧的格子是起始格。它在关闭列表里,所以我们也跳过它。
其他4格已经在开启列表里了,于是我们检查G值来判定,如果通过这一格到达那里,路径是否更好。我们来看选中格子下面的方格。它的G值是14。如果我们从当前格移动到那里,G值就会等于20(到达当前格的G值是10,移动到上面的格子将使得G值增加10)。因为G值20大于14,所以这不是更好的路径。如果你看图,就能理解。与其通过先水平移动一格,再垂直移动一格,还不如直接沿对角线方向移动一格来得简单。
当我们对已经存在于开启列表中的4个临近格重复这一过程的时候,我们发现没有一条路径可以通过使用当前格子得到改善,所以我们不做任何改变。既然我们已经检查过了所有邻近格,那么就可以移动到下一格了。
于是我们检索开启列表,现在里面只有7格了,我们仍然选择其中F值最低的。有趣的是,这次,有两个格子的数值都是54。我们如何选择?这并不麻烦。从速度上考虑,选择最后添加进列表的格子会更快捷。这种导致了寻路过程中,在靠近目标的时候,优先使用新找到的格子的偏好。但这无关紧要。(对相同数值的不同对待,导致不同版本的A*算法找到等长的不同路径。)
那我们就选择起始格右下方的格子,如图。
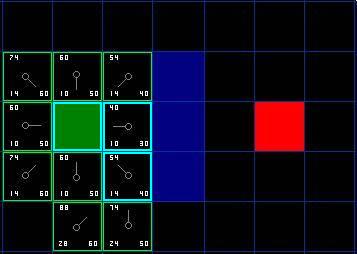
[图5]
这次,当我们检查相邻格的时候,发现右侧是墙,于是略过。上面一格也被略过。我们也略过了墙下面的格子。为什么呢?因为你不能在不穿越墙角的情况下直接到达那个格子。你的确需要先往下走然后到达那一格,按部就班的走过那个拐角。(注解:穿越拐角的规则是可选的。它取决于你的节点是如何放置的。)
这样一来,就剩下了其他5格。当前格下面的另外两个格子目前不在开启列表中,于是我们添加他们,并且把当前格指定为他们的父节点。其余3格,两个已经在关闭列表中(起始格,和当前格上方的格子,在表格中蓝色高亮显示),于是我们略过它们。最后一格,在当前格的左侧,将被检查通过这条路径,G值是否更低。不必担心,我们已经准备好检查开启列表中的下一格了。
我们重复这个过程,直到目标格被添加进关闭列表(注解),就如在下面的图中所看到的。
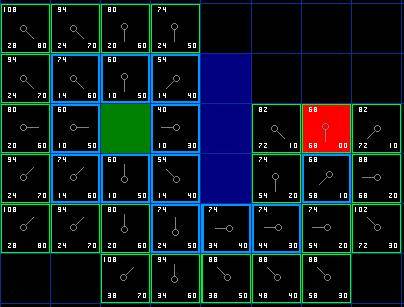
[图6]
注意,起始格下方格子的父节点已经和前面不同的。之前它的G值是28,并且指向右上方的格子。现在它的G值是20,指向它上方的格子。这在寻路过程中的某处发生,当应用新路径时,G值经过检查变得低了-于是父节点被重新指定,G和F值被重新计算。尽管这一变化在这个例子中并不重要,在很多场合,这种变化会导致寻路结果的巨大变化。
那么,我们怎么确定这条路径呢?很简单,从红色的目标格开始,按箭头的方向朝父节点移动。这最终会引导你回到起始格,这就是你的路径!看起来应该像图中那样。从起始格A移动到目标格B只是简单的从每个格子(节点)的中点沿路径移动到下一个,直到你到达目标点。就这么简单。
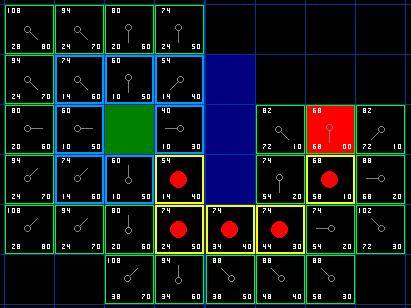
[图7]
A*方法总结
好,现在你已经看完了整个说明,让我们把每一步的操作写在一起:
1,把起始格添加到开启列表。
2,重复如下的工作:
a) 寻找开启列表中F值最低的格子。我们称它为当前格。
b) 把它切换到关闭列表。
c) 对相邻的8格中的每一个?
* 如果它不可通过或者已经在关闭列表中,略过它。反之如下。
* 如果它不在开启列表中,把它添加进去。把当前格作为这一格的父节点。记录这一格的F,G,和H值。
* 如果它已经在开启列表中,用G值为参考检查新的路径是否更好。更低的G值意味着更好的路径。如果是这样,就把这一格的父节点改成当前格,并且重新计算这一格的G和F值。如果你保持你的开启列表按F值排序,改变之后你可能需要重新对开启列表排序。
d) 停止,当你
* 把目标格添加进了关闭列表(注解),这时候路径被找到,或者
* 没有找到目标格,开启列表已经空了。这时候,路径不存在。
3.保存路径。从目标格开始,沿着每一格的父节点移动直到回到起始格。这就是你的路径。
(注解:在这篇文章的较早版本中,建议的做法是当目标格(或节点)被加入到开启列表,而不是关闭列表的时候停止寻路。这么做会更迅速,而且几乎总是能找到最短的路径,但不是绝对的。当从倒数第二个节点到最后一个(目标节点)之间的移动耗费悬殊很大时-例如刚好有一条河穿越两个节点中间,这时候旧的做法和新的做法就会有显著不同。)
题外话
离题一下,见谅,值得一提的是,当你在网上或者相关论坛看到关于A*的不同的探讨,你有时会看到一些被当作A*算法的代码而实际上他们不是。要使用 A*,你必须包含上面讨论的所有元素--特定的开启和关闭列表,用F,G和H作路径评价。有很多其他的寻路算法,但他们并不是A*,A*被认为是他们当中最好的。Bryan Stout在这篇文章后面的参考文档中论述了一部分,包括他们的一些优点和缺点。有时候特定的场合其他算法会更好,但你必须很明确你在作什么。好了,够多的了。回到文章。
实现的注解
现在你已经明白了基本原理,写你的程序的时候还得考虑一些额外的东西。下面这些材料中的一些引用了我用C++和Blitz Basic写的程序,但对其他语言写的代码同样有效。
1.其他单位(避免碰撞):如果你恰好看了我的例子代码,你会发现它完全忽略了其他单位。我的寻路者事实上可以相互穿越。取决于具体的游戏,这也许可以,也许不行。如果你打算考虑其他单位,希望他们能互相绕过,我建议你只考虑静止或那些在计算路径时临近当前单位的单位,把它们当前的位置标志为可通过的。对于临近的运动着的单位,你可以通过惩罚它们各自路径上的节点,来鼓励这些寻路者找到不同的路径(更多的描述见#2).
如果你选择了把其他正在移动并且远离当前寻路单位的那些单位考虑在内,你将需要实现一种方法及时预测在何时何地碰撞可能会发生,以便恰当的避免。否则你极有可能得到一条怪异的路径,单位突然转弯试图避免和一个已经不存在的单位发生碰撞。
当然,你也需要写一些碰撞检测的代码,因为无论计算的时候路径有多完美,它也会因时间而改变。当碰撞发生时,一个单位必须寻找一条新路径,或者,如果另一个单位正在移动并且不是正面碰撞,在继续沿当前路径移动之前,等待那个单位离开。
这些提示大概可以让你开始了。如果你想了解更多,这里有些你可能会觉得有用的链接:
* 自治角色的指导行为:Craig Reynold在指导能力上的工作和寻路有些不同,但是它可以和寻路整合从而形成更完整的移动和碰撞检测系统。
* 电脑游戏中的长短距指导:指导和寻路方面著作的一个有趣的考察。这是一个pdf文件。
* 协同单位移动:一个两部分系列文章的第一篇,内容是关于编队和基于分组的移动,作者是帝国时代(Age of Empires)的设计者Dave Pottinger.
* 实现协同移动:Dave Pottinger文章系列的第二篇。
2. 不同的地形损耗:在这个教程和我附带的程序中,地形只能是二者之-可通过的和不可通过的。但是你可能会需要一些可通过的地形,但是移动耗费更高-沼泽,小山,地牢的楼梯,等等。这些都是可通过但是比平坦的开阔地移动耗费更高的地形。类似的,道路应该比自然地形移动耗费更低。
这个问题很容易解决,只要在计算任何地形的G值的时候增加地形损耗就可以了。简单的给它增加一些额外的损耗就可以了。由于A*算法已经按照寻找最低耗费的路径来设计,所以很容易处理这种情况。在我提供的这个简单的例子里,地形只有可通过和不可通过两种,A*会找到最短,最直接的路径。但是在地形耗费不同的场合,耗费最低的路径也许会包含很长的移动距离-就像沿着路绕过沼泽而不是直接穿过它。
一种需额外考虑的情况是被专家称之为“influence mapping”的东西(暂译为影响映射图)。就像上面描述的不同地形耗费一样,你可以创建一格额外的分数系统,并把它应用到寻路的AI中。假设你有一张有大批寻路者的地图,他们都要通过某个山区。每次电脑生成一条通过那个关口的路径,它就会变得更拥挤。如果你愿意,你可以创建一个影响映射图对有大量屠杀事件的格子施以不利影响。这会让计算机更倾向安全些的路径,并且帮助它避免总是仅仅因为路径短(但可能更危险)而持续把队伍和寻路者送到某一特定路径。
另一个可能得应用是惩罚周围移动单位路径上得节点。A*的一个底限是,当一群单位同时试图寻路到接近的地点,这通常会导致路径交叠。以为一个或者多个单位都试图走相同或者近似的路径到达目的地。对其他单位已经“认领”了的节点增加一些惩罚会有助于你在一定程度上分离路径,降低碰撞的可能性。然而,如果有必要,不要把那些节点看成不可通过的,因为你仍然希望多个单位能够一字纵队通过拥挤的出口。同时,你只能惩罚那些临近单位的路径,而不是所有路径,否则你就会得到奇怪的躲避行为例如单位躲避路径上其他已经不在那里的单位。 还有,你应该只惩罚路径当前节点和随后的节点,而不应处理已经走过并甩在身后的节点。
3. 处理未知区域:你是否玩过这样的PC游戏,电脑总是知道哪条路是正确的,即使它还没有侦察过地图?对于游戏,寻路太好会显得不真实。幸运的是,这是一格可以轻易解决的问题。
答案就是为每个不同的玩家和电脑(每个玩家,而不是每个单位--那样的话会耗费大量的内存)创建一个独立的“knownWalkability”数组,每个数组包含玩家已经探索过的区域,以及被当作可通过区域的其他区域,直到被证实。用这种方法,单位会在路的死端徘徊并且导致错误的选择直到他们在周围找到路。一旦地图被探索了,寻路就像往常那样进行。
4. 平滑路径:尽管A*提供了最短,最低代价的路径,它无法自动提供看起来平滑的路径。看一下我们的例子最终形成的路径(在图7)。最初的一步是起始格的右下方,如果这一步是直接往下的话,路径不是会更平滑一些吗?
有几种方法来解决这个问题。当计算路径的时候可以对改变方向的格子施加不利影响,对G值增加额外的数值。也可以换种方法,你可以在路径计算完之后沿着它跑一遍,找那些用相邻格替换会让路径看起来更平滑的地方。想知道完整的结果,查看Toward More Realistic Pathfinding,一篇(免费,但是需要注册)Marco Pinter发表在Gamasutra.com的文章
5. 非方形搜索区域:在我们的例子里,我们使用简单的2D方形图。你可以不使用这种方式。你可以使用不规则形状的区域。想想冒险棋的游戏,和游戏中那些国家。你可以设计一个像那样的寻路关卡。为此,你可能需要建立一个国家相邻关系的表格,和从一个国家移动到另一个的G值。你也需要估算H值的方法。其他的事情就和例子中完全一样了。当你需要向开启列表中添加新元素的时候,不需使用相邻的格子,取而代之的是从表格中寻找相邻的国家。
类似的,你可以为一张确定的地形图创建路径点系统,路径点一般是路上,或者地牢通道的转折点。作为游戏设计者,你可以预设这些路径点。两个路径点被认为是相邻的如果他们之间的直线上没有障碍的话。在冒险棋的例子里,你可以保存这些相邻信息在某个表格里,当需要在开启列表中添加元素的时候使用它。然后你就可以记录关联的G值(可能使用两点间的直线距离),H值(可以使用到目标点的直线距离),其他都按原先的做就可以了。
Amit Patel 写了其他方法的摘要。另一个在非方形区域搜索RPG地图的例子,查看我的文章Two-Tiered A* Pathfinding。(译者注:译文: A*分层寻路)
6. 一些速度方面的提示:当你开发你自己的A*程序,或者改写我的,你会发现寻路占据了大量的CPU时间,尤其是在大地图上有大量对象在寻路的时候。如果你阅读过网上的其他材料,你会明白,即使是开发了星际争霸或帝国时代的专家,这也无可奈何。如果你觉得寻路太过缓慢,这里有一些建议也许有效:
* 使用更小的地图或者更少的寻路者。
* 不要同时给多个对象寻路。取而代之的是把他们加入一个队列,把寻路过程分散在几个游戏周期中。如果你的游戏以40周期每秒的速度运行,没人能察觉。但是当大量寻路者计算自己路径的时候,他们会发觉游戏速度突然变慢。
* 尽量使用更大的地图网格。这降低了寻路中搜索的总网格数。如果你有志气,你可以设计两个或者更多寻路系统以便使用在不同场合,取决于路径的长度。这也正是专业人士的做法,用大的区域计算长的路径,然后在接近目标的时候切换到使用小格子/区域的精细寻路。如果你对这个观点感兴趣,查阅我的文章Two-Tiered A* Pathfinding。(译者注:译文 :A*分层寻路)
* 使用路径点系统计算长路径,或者预先计算好路径并加入到游戏中。
* 预处理你的地图,表明地图中哪些区域是不可到达的。我把这些区域称作“孤岛”。事实上,他们可以是岛屿或其他被墙壁包围等无法到达的任意区域。A*的下限是,当你告诉它要寻找通往那些区域的路径时,它会搜索整个地图,直到所有可到达的方格/节点都被通过开启列表和关闭列表的计算。这会浪费大量的CPU时间。可以通过预先确定这些区域(比如通过flood-fill或类似的方法)来避免这种情况的发生,用某些种类的数组记录这些信息,在开始寻路前检查它。
* 在一个拥挤的类似迷宫的场合,把不能连通的节点看作死端。这些区域可以在地图编辑器中预先手动指定,或者如果你有雄心壮志,开发一个自动识别这些区域的算法。给定死端的所有节点可以被赋予一个唯一的标志数字。然后你就可以在寻路过程中安全的忽略所有死端,只有当起点或者终点恰好在死端的某个节点的时候才需要考虑它们。
7. 维护开启列表:这是A*寻路算法最重要的组成部分。每次你访问开启列表,你都需要寻找F值最低的方格。有几种不同的方法实现这一点。你可以把路径元素随意保存,当需要寻找F值最低的元素的时候,遍历开启列表。这很简单,但是太慢了,尤其是对长路径来说。这可以通过维护一格排好序的列表来改善,每次寻找F值最低的方格只需要选取列表的首元素。当我自己实现的时候,这种方法是我的首选。
在小地图。这种方法工作的很好,但它并不是最快的解决方案。更苛求速度的A*程序员使用叫做二叉堆的方法,这也是我在代码中使用的方法。凭我的经验,这种方法在大多数场合会快2~3倍,并且在长路经上速度呈几何级数提升(10倍以上速度)。如果你想了解更多关于二叉堆的内容,查阅我的文章,Using Binary Heaps in A* Pathfinding。(译者注:译文:在A*寻路中使用二叉堆)
另一个可能的瓶颈是你在多次寻路之间清除和保存你的数据结构的方法。我个人更倾向把所有东西都存储在数组里面。虽然节点可以以面向对象的风格被动态的产生,记录和保存,我发现创建和删除对象所增加的大量时间,以及多余的管理层次减慢的整个过程的速度。但是,如果你使用数组,你需要在调用之间清理数据。这中情形你想做的最后一件事就是在寻路调用之后花点时间把一切归零,尤其是你的地图很大的时候。
我通过使用一个叫做whichList(x,y)的二维数组避免这种开销,数组的每个元素表明了节点在开启列表还是在关闭列表中。尝试寻路之后,我没有清零这个数组。取而代之的是,我在新的寻路中重置onClosedList和onOpenList的数值,每次寻路两个都+5或者类似其他数值。这种方法,算法可以安全的跳过前面寻路留下的脏数据。我还在数组中储存了诸如F,G和H的值。这样一来,我只需简单的重写任何已经存在的值而无需被清除数组的操作干扰。将数据存储在多维数组中需要更多内存,所以这里需要权衡利弊。最后,你应该使用你最得心应手的方法。
8. Dijkstra的算法:尽管A*被认为是通常最好的寻路算法(看前面的“题外话”),还是有一种另外的算法有它的可取之处-Dijkstra算法。 Dijkstra算法和A*本质是相同的,只有一点不同,就是Dijkstra算法没有启发式(H值总是0)。由于没有启发式,它在各个方向上平均搜索。正如你所预料,由于Dijkstra算法在找到目标前通常会探索更大的区域,所以一般会比A*更慢一些。
那么为什么要使用这种算法呢?因为有时候我们并不知道目标的位置。比如说你有一个资源采集单位,需要获取某种类型的资源若干。它可能知道几个资源区域,但是它想去最近的那个。这种情况,Dijkstra算法就比A*更适合,因为我们不知道哪个更近。用A*,我们唯一的选择是依次对每个目标许路并计算距离,然后选择最近的路径。我们寻找的目标可能会有不计其数的位置,我们只想找其中最近的,而我们并不知道它在哪里,或者不知道哪个是最近的。
进一步的阅读
好,现在你对一些进一步的观点有了初步认识。这时,我建议你研究我的源代码。包里面包含两个版本,一个是用C++写的,另一个用Blitz Basic。顺便说一句,两个版本都注释详尽,容易阅读,这里是链接。
* 例子代码: A* Pathfinder (2D) Version 1.9
如果你既不用C++也不用Blitz Basic,在C++版本里有两个小的可执行文件。Blitz Basic可以在从Blitz Basic网站免费下载的Blitz Basic 3D(不是Blitz Plus)演示版上运行。Ben O'Neill提供一个联机演示可以在这里找到。
你也该看看以下的网页。读了这篇教程后,他们应该变得容易理解多了。
* Amit的 A* 页面:这是由Amit Patel制作,被广泛引用的页面,如果你没有事先读这篇文章,可能会有点难以理解。值得一看。尤其要看Amit关于这个问题的自己的看法。
* Smart Moves:智能寻路:Bryan Stout发表在Gamasutra.com的这篇文章需要注册才能阅读。注册是免费的而且比起这篇文章和网站的其他资源,是非常物有所值的。Bryan用Delphi写的程序帮助我学习A*,也是我的A*代码的灵感之源。它还描述了A*的几种变化。
* 地形分析:这是一格高阶,但是有趣的话题,Dave Pottinge撰写,Ensemble Studios的专家。这家伙参与了帝国时代和君王时代的开发。别指望看懂这里所有的东西,但是这是篇有趣的文章也许会让你产生自己的想法。它包含一些对 mip-mapping,influence mapping以及其他一些高级AI/寻路观点。对"flood filling"的讨论使我有了我自己的“死端”和“孤岛”的代码的灵感,这些包含在我Blitz版本的代码中。
其他一些值得一看的网站:
* aiGuru: Pathfinding
* Game AI Resource: Pathfinding
* GameDev.net: Pathfinding
我同样高度推荐下面这几本书, 里面有很多关于寻路和其他AI话题的文章。 它们也附带了实例代码的CD。这些书我都买了。另外,如果你通过下面的链接购买了它们,我会从Amazon得到几个美分。:)
好了,这就是全部。如果你刚好写一个运用这些观点的程序,我想拜读一下。你可以这样联系我:

现在,好运!
译者参考文献:
在A*寻路中使用二叉堆
A*分层寻
游戏算法整理 算法二:碰撞
1. 碰撞检测和响应
碰撞在游戏中运用的是非常广泛的,运用理论实现的碰撞,再加上一些小技巧,可以让碰撞检测做得非常精确,效率也非常高。从而增加游戏的功能和可玩性。
2D碰撞检测
2D的碰撞检测已经非常稳定,可以在许多著作和论文中查询到。3D的碰撞还没有找到最好的方法,现在使用的大多数方法都是建立在2D基础上的。
碰撞检测
碰撞的检测不仅仅是运用在游戏中,事实上,一开始的时候是运用在模拟和机器人技术上的。这些工业上的碰撞检测要求非常高,而碰撞以后的响应也是需要符合现实生活的,是需要符合人类常规认识的。游戏中的碰撞有些许的不一样,况且,更重要的,我们制作的东西充其量是商业级别,还不需要接触到纷繁复杂的数学公式。
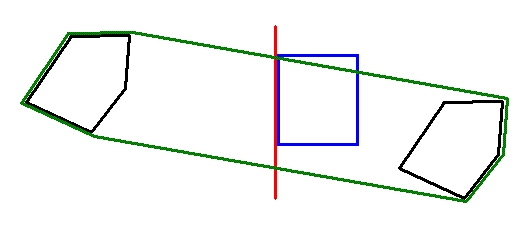
图1
最理想的碰撞,我想莫过于上图,完全按照多边形的外形和运行路径规划一个范围,在这个范围当中寻找会产生阻挡的物体,不管是什么物体,产生阻挡以后,我们运动的物体都必须在那个位置产生一个碰撞的事件。最美好的想法总是在实现上有一些困难,事实上我们可以这么做,但是效率却是非常非常低下的,游戏中,甚至于工业中无法忍受这种速度,所以我们改用其它的方法来实现。

图2
最简单的方法如上图,我们寻找物体的中心点,然后用这个中心点来画一个圆,如果是一个3D的物体,那么我们要画的就是一个球体。在检测物体碰撞的时候,我们只要检测两个物体的半径相加是否大于这两个物体圆心的实际距离。
这个算法是最简单的一种,现在还在用,但是不是用来做精确的碰撞检测,而是用来提高效率的模糊碰撞检测查询,到了这个范围以后,再进行更加精密的碰撞检测。一种比较精密的碰撞检测查询就是继续这种画圆的思路,然后把物体细分,对于物体的每个部件继续画圆,然后再继续进行碰撞检测,直到系统规定的,可以容忍的误差范围以后才触发碰撞事件,进行碰撞的一些操作。
有没有更加简单的方法呢?2D游戏中有许多图片都是方方正正的,所以我们不必把碰撞的范围画成一个圆的,而是画成一个方的。这个正方形,或者说是一个四边形和坐标轴是对齐的,所以运用数学上的一些方法,比如距离计算等还是比较方便的。这个检测方法就叫AABBs(Axis-aligned Bounding Boxes)碰撞检测,游戏中已经运用的非常广泛了,因为其速度快,效率高,计算起来非常方便,精确度也是可以忍受的。
做到这一步,许多游戏的需求都已经满足了。但是,总是有人希望近一步优化,而且方法也是非常陈旧的:继续对物体的各个部分进行细分,对每个部件做AABB 的矩形,那这个优化以后的系统就叫做OBB系统。虽然说这个优化以后的系统也不错,但是,许多它可以运用到的地方,别人却不爱使用它,这是后面会继续介绍的地方。
John Carmack不知道看的哪本书,他早在DOOM中已经使用了BSP系统(二分空间分割),再加上一些小技巧,他的碰撞做得就非常好了,再加上他发明的 castray算法,DOOM已经不存在碰撞的问题,解决了这样的关键技术,我想他不再需要在什么地方分心了,只要继续研究渲染引擎就可以了。(Windows游戏编程大师技巧P392~P393介绍)(凸多边形,多边形退化,左手定律)SAT系统非常复杂,是SHT(separating hyperplane theorem,分离超平面理论)的一种特殊情况。这个理论阐述的就是两个不相关的曲面,是否能够被一个超平面所分割开来,所谓分割开来的意思就是一个曲面贴在平面的一边,而另一个曲面贴在平面的另一边。我理解的就是有点像相切的意思。SAT是SHT的特殊情况,所指的就是两个曲面都是一些多边形,而那个超平面也是一个多边形,这个超平面的多边形可以在场景中的多边形列表中找到,而超平面可能就是某个多边形的表面,很巧的就是,这个表面的法线和两个曲面的切面是相对应的。接下来的证明,我想是非常复杂的事情,希望今后能够找到源代码直接运用上去。而我们现在讲究的快速开发,我想AABB就足以满足了。
3D碰撞检测
3D的检测就没有什么很标准的理论了,都建立在2D的基础上,我们可以沿用AABB或者OBB,或者先用球体做粗略的检测,然后用AABB和OBB作精细的检测。BSP技术不流行,但是效率不错。微软提供了D3DIntersect函数让大家使用,方便了许多,但是和通常一样,当物体多了以后就不好用了,明显的就是速度慢许多。
碰撞反应
碰撞以后我们需要做一些反应,比如说产生反冲力让我们反弹出去,或者停下来,或者让阻挡我们的物体飞出去,或者穿墙,碰撞最讨厌的就是穿越,本来就不合逻辑,查阅了那么多资料以后,从来没有看到过需要穿越的碰撞,有摩擦力是另外一回事。首先看看弹性碰撞。弹性碰撞就是我们初中物理中说的动量守恒。物体在碰撞前后的动量守恒,没有任何能量损失。这样的碰撞运用于打砖块的游戏中。引入质量的话,有的物体会是有一定的质量,这些物体通常来说是需要在碰撞以后进行另外一个方向的运动的,另外一些物体是设定为质量无限大的,这些物体通常是碰撞墙壁。
当物体碰到质量非常大的物体,默认为碰到了一个弹性物体,其速度会改变,但是能量不会受到损失。一般在代码上的做法就是在速度向量上加上一个负号。
绝对的弹性碰撞是很少有的,大多数情况下我们运用的还是非弹性碰撞。我们现在玩的大多数游戏都用的是很接近现实的非弹性碰撞,例如Pain-Killer 中的那把吸力枪,它弹出去的子弹吸附到NPC身上时的碰撞响应就是非弹性碰撞;那把残忍的分尸刀把墙打碎的初始算法就是一个非弹性碰撞,其后使用的刚体力学就是先建立在这个算法上的。那么,是的,如果需要非弹性碰撞,我们需要介入摩擦力这个因素,而我们也无法简单使用动量守恒这个公式。
我们可以采取比较简单的方法,假设摩擦系数μ非常大,那么只要物体接触,并且拥有一个加速度,就可以产生一个无穷大的摩擦力,造成物体停止的状态。
基于别人的引擎写出一个让自己满意的碰撞是不容易的,那么如果自己建立一个碰撞系统的话,以下内容是无法缺少的:
– 一个能够容忍的碰撞系统
– 一个从概念上可以接受的物理系统
– 质量
– 速度
– 摩擦系数
– 地心引力
http://www.gamasutra.com/features/20000330/bobic_01.htm
http://www.gamasutra.com/features/20000330/bobic_02.htm
http://www.gamasutra.com/features/20000330/bobic_03.htm
这三篇是高级碰撞检测。
游戏算法整理 算法三:寻路算法新思维
目前常用寻路算法是A*方式,原理是通过不断搜索逼近目的地的路点来获得。
如果通过图像模拟搜索点,可以发现:非启发式的寻路算法实际上是一种穷举法,通过固定顺序依次搜索人物周围的路点,直到找到目的地,搜索点在图像上的表现为一个不断扩大的矩形。如下:
 
很快人们发现如此穷举导致搜索速度过慢,而且不是很符合逻辑,试想:如果要从(0,0)点到达(100,0)点,如果每次向东搜索时能够走通,那么干吗还要搜索其他方向呢?所以,出现了启发式的A*寻路算法,一般通过 已经走过的路程 + 到达目的地的直线距离 代价值作为搜索时的启发条件,每个点建立一个代价值,每次搜索时就从代价低的最先搜索,如下:
 
综上所述,以上的搜索是一种矩阵式的不断逼近终点的搜索做法。优点是比较直观,缺点在于距离越远、搜索时间越长。
现在,我提出一种新的AI寻路方式——矢量寻路算法。
通过观察,我们可以发现,所有的最优路线,如果是一条折线,那么、其每一个拐弯点一定发生在障碍物的突出边角,而不会在还没有碰到障碍物就拐弯的情况:如下图所示:
我们可以发现,所有的红色拐弯点都是在障碍物(可以认为是一个凸多边形)的顶点处,所以,我们搜索路径时,其实只需要搜索这些凸多边形顶点不就可以了吗?如果将各个顶点连接成一条通路就找到了最优路线,而不需要每个点都检索一次,这样就大大减少了搜索次数,不会因为距离的增大而增大搜索时间。
这种思路我尚未将其演变为算法,姑且提出一个伪程序给各位参考:
1.建立各个凸多边形顶点的通路表TAB,表示顶点A到顶点B是否可达,将可达的顶点分组保存下来。如: ( (0,0) (100,0) ),这一步骤在程序刚开始时完成,不要放在搜索过程中空耗时间。
2.开始搜索A点到B点的路线
3.检测A点可以直达凸多边形顶点中的哪一些,挑选出最合适的顶点X1。
4.检测与X1相连(能够接通)的有哪些顶点,挑出最合适的顶点X2。
5.X2是否是终点B?是的话结束,否则转步骤4(X2代入X1)
如此下来,搜索只发生在凸多边形的顶点,节省了大量的搜索时间,而且找到的路线无需再修剪锯齿,保证了路线的最优性。
这种方法搜索理论上可以减少大量搜索点、缺点是需要实现用一段程序得出TAB表,从本质上来说是一种空间换时间的方法,而且搜索时A*能够用的启发条件,在矢量搜索时依然可以使用。
游戏算法整理 算法四:战略游戏中的战争模型算法的初步探讨
《三国志》系列游戏相信大家都有所了解,而其中的(宏观)战斗时关于双方兵力,士气,兵种克制,攻击力,增援以及随战争进行兵力减少等数值的算法是十分值得研究的。或许是由于简单的缘故,我在网上几乎没有找到相关算法的文章。下面给出这个战争的数学模型算法可以保证游戏中战争的游戏性与真实性兼顾,希望可以给有需要这方面开发的人一些启迪。
假设用x(t)和y(t)表示甲乙交战双方在t时刻的兵力,如果是开始时可视为双方士兵人数。
假设每一方的战斗减员率取决于双方兵力和战斗力,用f(x,y)和g(x,y)表示,每一方的增援率是给定函数用u(t)和v(t)表示。
如果双方用正规部队作战(可假设是相同兵种),先分析甲方的战斗减员率f(x,y)。可知甲方士兵公开活动,处于乙方没一个士兵的监视和杀伤范围之内,一但甲方的某个士兵被杀伤,乙方的火力立即集中在其余士兵身上,所以甲方的战斗减员率只与乙方的兵力有关可射为f与y成正比,即f=ay,a表示乙方平均每个士兵对甲方士兵的杀伤率(单位时间的杀伤数),成为乙方的战斗有效系数。类似g= -bx
这个战争模型模型方程1为
x’(t)= -a*y(t)+u(t) x’(t)是x(t)对于t 的导数
y’(t)= -b*x(t)+v(t) y’(t)是y(t)对于t的导数
利用给定的初始兵力,战争持续时间,和增援兵力可以求出双方兵力在战争中的变化函数。
(本文中解法略)
如果考虑由于士气和疾病等引起的非战斗减员率(一般与本放兵力成正比,设甲乙双方分别为h,w)
可得到改进战争模型方程2:
x’(t)= -a*y(t)-h*x(t)+u(t)
y’(t)= -b*x(t)-w*y(t)+v(t)
利用初始条件同样可以得到双方兵力在战争中的变化函数和战争结果。
此外还有不同兵种作战(兵种克制)的数学模型:
模型1中的战斗有效系数a可以进一步分解为a=ry*py*(sry/sx),其中ry是乙方的攻击率(每个士兵单位的攻击次数),py是每次攻击的命中率。(sry/sx)是乙方攻击的有效面积sry与甲方活动范围sx之比。类似甲方的战斗有效系数b=rx*px*(srx/sy),rx和px是甲方的攻击率和命中率,(srx/sy)是甲方攻击的有效面积与乙方活动范围sy之比。由于增加了兵种克制的攻击范围,所以战斗减员率不光与对方兵力有关,而且随着己放兵力增加而增加。因为在一定区域内,士兵越多被杀伤的就越多。
方程
x’(t)= -ry*py*(sry/sx)*x(t)*y(t)-h*x(t)+u(t)
y’(t)= -rx*px*(srx/sy)*x(t)*y(t)-w*y(t)+u(t)
游戏算法整理 算法五:飞行射击游戏中的碰撞检测
在游戏中物体的碰撞是经常发生的,怎样检测物体的碰撞是一个很关键的技术问题。在RPG游戏中,一般都将场景分为许多矩形的单元,碰撞的问题被大大的简化了,只要判断精灵所在的单元是不是有其它的东西就可以了。而在飞行射击游戏(包括象荒野大镖客这样的射击游戏)中,碰撞却是最关键的技术,如果不能很好的解决,会影响玩游戏者的兴趣。因为飞行射击游戏说白了就是碰撞的游戏——躲避敌人的子弹或飞机,同时用自己的子弹去碰撞敌人。
碰撞,这很简单嘛,只要两个物体的中心点距离小于它们的半径之和就可以了。确实,而且我也看到很多人是这样做的,但是,这只适合圆形的物体——圆形的半径处处相等。如果我们要碰撞的物体是两艘威力巨大的太空飞船,它是三角形或矩形或其他的什么形状,就会出现让人尴尬的情景:两艘飞船眼看就要擦肩而过,却出人意料的发生了爆炸;或者敌人的子弹穿透了你的飞船的右弦,你却安然无恙,这不是我们希望发生的。于是,我们需要一种精确的检测方法。
那么,怎样才能达到我们的要求呢?其实我们的前辈们已经总结了许多这方面的经验,如上所述的半径检测法,三维中的标准平台方程法,边界框法等等。大多数游戏程序员都喜欢用边界框法,这也是我采用的方法。边界框是在编程中加进去的不可见的边界。边界框法,顾名思义,就是用边界框来检测物体是否发生了碰撞,如果两个物体的边界框相互干扰,则发生了碰撞。用什么样的边界框要视不同情况而定,用最近似的几何形状。当然,你可以用物体的准确几何形状作边界框,但出于效率的考虑,我不赞成这样做,因为游戏中的物体一般都很复杂,用复杂的边界框将增加大量的计算,尤其是浮点计算,而这正是我们想尽量避免的。但边界框也不能与准确几何形状有太大的出入,否则就象用半径法一样出现奇怪的现象。
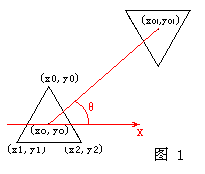
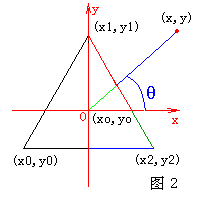
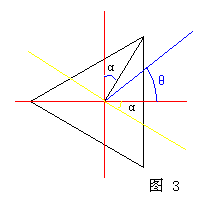
在飞行射击游戏中,我们的飞机大多都是三角形的,我们可以用三角形作近似的边界框。现在我们假设飞机是一个正三角形(或等要三角形,我想如果谁把飞机设计成左右不对称的怪物,那他的审美观一定有问题),我的飞机是正着的、向上飞的三角形,敌人的飞机是倒着的、向下飞的三角形,且飞机不会旋转(大部分游戏中都是这样的)。我们可以这样定义飞机:中心点O(Xo,Yo),三个顶点P0(X0,Y0)、P1(X1,Y1)、P2(X2,Y2)。中心点为正三角形的中心点,即中心点到三个顶点的距离相等。接下来的问题是怎样确定两个三角形互相干扰了呢?嗯,现在我们接触到问题的实质了。如果你学过平面解析几何,我相信你可以想出许多方法解决这个问题。判断一个三角形的各个顶点是否在另一个三角形里面,看起来是个不错的方法,你可以这样做,但我却发现一个小问题:一个三角形的顶点没有在另一个三角形的里面,却可能发生了碰撞,因为另一个三角形的顶点在这个三角形的里面,所以要判断两次,这很麻烦。有没有一次判断就可以的方法?我们把三角形放到极坐标平面中,中心点为原点,水平线即X轴为零度角。我们发现三角形成了这个样子:在每个角度我们都可以找到一个距离,用以描述三角形的边。既然我们找到了边到中心点的距离,那就可以用这个距离来检测碰撞。如图一,两个三角形中心点坐标分别为(Xo,Yo)和 (Xo1,Yo1),由这两个点的坐标求出两点的距离及两点连线和X轴的夹角θ,再由θ求出中心点连线与三角形边的交点到中心点的距离,用这个距离与两中心点距离比较,从而判断两三角形是否碰撞。因为三角形左右对称,所以θ取-90~90度区间就可以了。哈,现在问题有趣多了,-90~90度区间正是正切函数的定义域,求出θ之后再找对应的边到中心点的距离就容易多了,利用几何知识,如图二,将三角形的边分为三部分,即图2中红绿蓝三部分,根据θ在那一部分而分别对待。用正弦定理求出边到中心点的距离,即图2中浅绿色线段的长度。但是,如果飞机每次移动都这样判断一次,效率仍然很低。我们可以结合半径法来解决,先用半径法判断是否可能发生碰撞,如果可能发生碰撞,再用上面的方法精确判断是不是真的发生了碰撞,这样基本就可以了。如果飞机旋转了怎么办呢,例如,如图三所示飞机旋转了一个角度α,仔细观察图三会发现,用(θ-α)就可以求出边到中心点的距离,这时你要注意边界情况,即(θ-α)可能大于90度或小于-90度。啰罗嗦嗦说了这么多,不知道大家明白了没有。我编写了一个简单的例程,用于说明我的意图。在例子中假设所有飞机的大小都一样,并且没有旋转。
/////////////////////////////////////////////////////////////////////
//example.cpp
//碰撞检测演示
//作者 李韬
/////////////////////////////////////////////////////////////////////
//限于篇幅,这里只给出了碰撞检测的函数
//define/////////////////////////////////////////////////////////////
#define NUM_VERTICES 3
#define ang_30 -0.5236
#define ang60 1.0472
#define ang120 2.0944
//deftype////////////////////////////////////////////////////////////
struct object
{
float xo, yo;
float radio;
float x_vel, y_vel;
float vertices[NUM_VERTICES][2];
}
//faction/////////////////////////////////////////////////////////////
//根据角度求距离
float AngToDis(struct object obj, float angle)
{
float dis, R;
R = obj.radius;
if (angle <= ang_30)
dis = R / (2 * sin(-angle));
else if (angle >= 0)
dis = R / (2 * sin(angle + ang60));
else dis = R / (2 * sin(ang120 - angle));
return dis;
}
//碰撞检测
int CheckHit(struct object obj1, struct object obj2)
{
float deltaX, deltaY, angle, distance, bumpdis;
deltaX = abs(obj1.xo - obj2.xo);
deltaY = obj1.yo - obj2.yo;
distance = sqrt(deltaX * deltaX + deltaY * deltaY);
if (distance <= obj.radio)
{
angle = atan2(deltaY, deltaX);
bumpdis1 = AngToDis(obj1, angle);
return (distance <= 2 * bumpdis);
}
ruturn 0;
}
//End//////////////////////////////////////////////////////////////
上面程序只是用于演示,并不适合放在游戏中,但你应该明白它的意思,以便写出适合你自己的碰撞检测。游戏中的情况是多种多样的,没有哪种方法能适应所有情况,你一定能根据自己的情况找到最适合自己的方法。
游戏算法整理 算法六:关于SLG中人物可到达范围计算的想法
下面的没有经过实践,因此很可能是错误的,觉得有用的初学朋友读一读吧:)
希望高人指点一二 :)
简介:
在标准的SLG游戏中,当在一个人物处按下鼠标时,会以人物为中心,向四周生成一个菱形的可移动区范围,如下:
0
000
00s00
000
0
这个图形在刚开始学习PASCAL时就应该写过一个画图的程序(是否有人怀念?)。那个图形和SLG的扩展路径一样。
一、如何生成路径:
从人物所在的位置开始,向四周的四个方向扩展,之后的点再进行扩展。即从人物所在的位置从近到远进行扩展(类似广宽优先)。
二、扩展时会遇到的问题:
1、当扩展到一个点时,人物的移动力没有了。
2、当扩展的时候遇到了一个障碍点。
3、当扩展的时候这个结点出了地图。
4、扩展的时候遇到了一个人物正好站在这个点(与2同?)。
5、扩展的点已经被扩展过了。当扩展节点的时候,每个节点都是向四周扩展,因此会产生重复的节点。
当遇到这些问题的时候,我们就不对这些节点处理了。在程序中使用ALLPATH[]数组记录下每一个等扩展的节点,不处理这些问题节点的意思就是不把它们加入到ALLPATH[]数组中。我们如何去扩展一个结点周围的四个结点,使用这个结点的坐标加上一个偏移量就可以了,方向如下:
3
0 2
1
偏移量定义如下:
int offx[4] = { -1, 0, 1, 0 };
int offy[4] = { 0, 1, 0, -1 };
扩展一个节点的相邻的四个节点的坐标为:
for(int i=0; i<4; i )
{
temp.x = temp1.x offx[i];
temp.y = temp1.y offy[i];
}
三、关于地图的结构:
1、地图的二维坐标,用于确定每个图块在地图中的位置。
2、SLG中还要引入一个变量decrease表示人物经过这个图块后他的移动力的减少值。例如,一个人物现在的移动力为CurMP=5,与之相领的图块的decrease=2;这时,如果人物移动到这里,那它的移动力变成CurMP-decrease。
3、Flag域:宽度优先中好像都有这个变量,有了它,每一个点保证只被扩展一次。防止一个点被扩展多次。(一个点只被扩展一次真的能得到正确的结果吗?)
4、一个地图上的图块是否可以通过,我们使用了一个Block代表。1---不可以通过;0---可以通过。
这样,我们可以定义一个简单的地图结构数组了:
#define MAP_MAX_WIDTH 50
#define MAP_MAX_HEIGHT 50
typedef struct tagTILE{
int x,y,decrease,flag,block;
}TILE,*LPTILE;
TILE pMap[MAP_MAX_WIDTH][MAP_MAX_HEIGHT];
以上是顺序数组,是否使用动态的分配更好些?毕竟不能事先知道一个地图的宽、高。
四、关于路径:
SLG游戏中的扩展路径是一片区域(以人物为中心向四周扩展,当然,当人物移动时路径只有一个)。这些扩展的路径必须要存储起来,所有要有一个好的结构。我定义了一个结构,不是很好:
typedef struct tagNODE{
int x,y; //扩展路径中的一个点在地图中的坐标。
int curmp; //人物到了这个点以后的当前的移动力。
}NODE,*LPNODE;
上面的结构是定义扩展路径中的一个点的结构。扩展路径是点的集合,因此用如下的数组进行定义:
NODE AllPath[PATH_MAX_LENGTH];
其中的PATH_MAX_LENGTH代表扩展路径的点的个数,我们不知道这个扩展的路径中包含多少个点,因此定义一个大一点的数字使这个数组不会产生溢出:
#define PATH_MAX_LENGTH 200
上面的这个数组很有用处,以后的扩展就靠它来实现,它应该带有两个变量nodecount 代表当前的数组中有多少个点。当然,数组中的点分成两大部分,一部分是已经扩展的结点,存放在数组的前面;另一部分是等扩展的节点,放在数组的后面为什么会出现已扩展节点和待扩展节点?如下例子:
当前的人物坐标为x,y;移动力为mp。将它存放到AllPath数组中,这时的起始节点为等扩展的节点。这时我们扩展它的四个方向,对于合法的节点(如没有出地图,也没有障碍......),我们将它们存放入AllPath数组中,这时的新加入的节点(起始节点的子节点)就是等扩展结点,而起始节点就成了已扩展节点了。下一次再扩展节点的时候,我们不能再扩展起始节点,因为它是已经扩展的节点了。我们只扩展那几个新加入的节点(待扩展节点),之后的情况以此类推。那么我们如何知道哪些是已经扩展的结点,哪些是等扩展的节点?我们使用另一个变量cutflag,在这个变量所代表的下标以前的结点是已扩展节点,在它及它之后是待扩展结点。
五、下面是基本框架(只扩展一个人物的可达范围):
int nodecount = 0; //AllPath数组中的点的个数(包含待扩展节点和已经扩展的节点
int cutflag = 0; //用于划分已经扩展的节点和待扩展节点
NODE temp; //路径中的一个点(临时)
temp.x = pRole[cur] - >x; //假设有一个关于人物的类,代表当前的人物
temp.y = pRole[cur] - >y;
temp.curmp = pRole[cur] - >MP; //人物的最大MP
AllPath[nodecount] = temp; //起始点入AllPath,此时的起始点为等扩展的节点
while (curflag < nodecount) { //数组中还有待扩展的节点
int n = nodecount; //记录下当前的数组节点的个数。
for (int i = cutflag; i < nodecount; i) { //遍历待扩展节点
for (int j = 0; j < 4; j) { //向待扩展节点的四周各走一步
//取得相邻点的数据
temp.x = AllPath[i].x offx[j];
temp.y = AllPath[i].y offy[j];
temp.curmp = AllPath[i].curmp -
pMap[AllPath[i].x][AllPath[i].y].decrease;
//以下为检测是否为问题点的过程,如果是问题点,不加入AllPath数组,继续处理其它的点
if (pMap[temp.x][temp.y].block) {
continue; //有障碍,处理下一个节点
}
if (temp.curmp < 0) {
continue; //没有移动力了
}
if (temp.x < 0 || temp.x >= MAP_MAX_WIDTH || temp.y < 0 ||
temp.y >= MAP_MAX_HEIGHT) {
continue; //出了地图的范围
}
if (pMap[temp.x][temp.y].flag) {
continue; //已经扩展了的结点
}
//经过了上面几层的检测,没有问题的节点过滤出来,可以加入AllPath
AllPath[nodecount] = temp;
}
pMap[AllPath[i].x][AllPath[i].y].flag = 1; //将已经扩展的节点标记为已扩展节点
}
cutflag = n; //将已扩展节点和待扩展节点的分界线下标值移动到新的分界线
}
for (int i = 0; i < nodecount; i) {
pMap[AllPath[i].x][AllPath[i].y].bFlag = 0; //标记为已扩展节点的标记设回为待扩展节点。
}
游戏算法整理 算法七 无限大地图的实现
这已经不是什么新鲜的东西了,不过现在实在想不到什么好写,而且版面上又异常冷清,我再不说几句就想要倒闭了一样。只好暂且拿这个东西来凑数吧。
无限大的地图,听上去非常吸引人。本来人生活的空间就是十分广阔的,人在这么广阔的空间里活动才有一种自由的感觉。游戏中的虚拟世界由于受到计算机存储空间的限制,要真实地反映这个无限的空间是不可能的。而对这个限制最大的,就是内存的容量了。所以在游戏的空间里,我们一般只能在一个狭小的范围里活动,在一般的RPG中,从一个场景走到另一个场景,即使两个地方是紧紧相连的,也要有一个场景的切换过程,一般的表现就是画面的淡入淡出。
这样的场景切换给人一种不连续的感觉(我不知道可不可以把这种称作“蒙太奇”:o)),从城内走到城外还有情可缘,因为有道城墙嘛,但是两个地方明明没有界限,却偏偏在这一边看不到另外一边,就有点不现实了。当然这并不是毛病,一直以来的RPG都是遵循这个原则,我们(至少是我)已经习惯了这种走路的方式。我在这里说的仅仅是另外一种看起来更自然一点的走路方式,仅此而已。
当然要把整个城市的地图一下子装进内存,现在的确是不现实的,每一次只能放一部分,那么应该怎么放才是我们要讨论的问题。
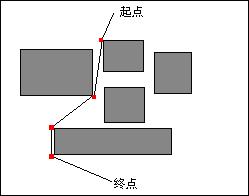
我们在以前提到Tile方法构造地图时就谈到过Tile的好处之一就是节省内存,这里仍然可以借鉴Tile的思想。我们把整个大地图分成几块,把每一块称作一个区域,在同一时间里,内存中只保存相邻的四块区域。这里每个区域的划分都有一定的要求:每个区域大小应该相等这是一定的了,不然判断当前屏幕在哪个区域中就成了一个非常令人挠头的事;另外每个区域的大小都要大于屏幕的大小,也只有这样才能保证屏幕(就是图中那块半透明的蓝色矩形)在地图上荡来荡去的时候,最多同时只能覆盖四个区域(象左图中所表示的),内存里也只要保存四个区域就足够了;还有一点要注意的,就是地图上的建筑物(也包括树啦,大石头啦什么的)必须在一个区域内,这样也是为了画起来方便,当然墙壁——就是那种连续的围墙可以除外,因为墙壁本来就是一段一段拼起来的。
我们在程序中可以设定4个指针来分别指向这4个区域,当每次主角移动时,就判断当前滚动的屏幕是否移出了这四个区域,如果移出了这四个区域,那么就废弃两个(或三个)已经在目前的四个相邻区域中被滚出去的区域(说得很别扭,各位见谅),读入两个(或三个)新滚进来的区域,并重新组织指针。这里并不涉及内存区域的拷贝。
这样的区域划分方法刚好适合我们以前提到的Tile排列方法,只要每个区域横向Tile的个数是个偶数就行了,这样相邻的两个区域拼接起来刚好严丝合缝,而且每个区域块的结构完全一致,没有那些需要重复保存的Tile(这个我想我不需要再画图说明了,大家自己随便画个草图就看得出来了)。在文件中的保存方法就是按一个个区域分别保存,这样在读取区域数据时就可以直接作为一整块读入,也简化了程序。另外还有个细节就是,我们的整个地图可能不是一个规则的矩形,可能有些地方是无法达到的,如右图所示,背景是黑色的部分代表人物不能达到的地方。那么在整个地图中,这一部分区域(在图中蓝色的3号区域)就可以省略,表现在文件存储上就是实际上不存储这一部分区域,这样可以节省下不少存储空间。对于这种地图可以用一个稀疏矩阵来存储,大家也可以发挥自己的才智用其他对于编程来说更方便的形式来存储地图。
这就是对无限大地图实现的一种方法,欢迎大家提出更好的方法。也希望整个版面能够活跃一点。
|