随笔档案

用途：对我来说，学习HMM是为了对以后的词性或概念标注打下理论基础
符号说明：
S：表示状态集合。S=[S₁,S₂,S₃....]。其中S_i表示第i个状态（第i种状态）
Q：表示系统实际的状态序列，Q=[q₁,q₂,....,q_T]。q1表示t=1时，系统所处的状态，如：q₁=S₃表示t=1时刻，系统状态为S₃。

1.离散马尔可夫过程
（1）定义：一个系统，在任一时刻t，可能处于N个不同状态S₁,S₂...S_N中的某一个。系统变化服从某种统计规律。如果系统状态序列满足下列无后效的条件，则称(q_t,t≥1)为离散的马尔可夫过程。
                                        P[q_t+1=S_j|q_t=S_i,q_t-1=S_k,...]=P[q_t+1=S_j|q_t=S_i]
    可见系统将来的状态仅与现在所处状态有关，与过去无关，这种情况称之为“无后效”。
    如果进一步有P[q_t+1=S_j|q_t=S_i]与时刻t无关，则称相应的马尔可夫过程是齐决的或是时齐的，引入记号：
                                        a_ij=P[q_t+1=S_j|q_t=S_i]，1≤i,j≤N
    注：这里有人也称a_ij为S_i→S_j的发射概率，也称转移概率。

（2）初始概率分布：         π_i=P[q₁=S_i],   1≤i,j≤N 
    k步转移概率：
        a_ij^(k)=P[q_t+k=S_j|q_t=S_i]
当k=1时，a_ij^(k)=a_ij⁽¹⁾=a_ij

（3）切普曼—柯尔莫哥洛夫公式（Chapman-Kolmogorol）
            

2.隐马尔可夫模型
    当状态本身是不可观察，从而得到隐马尔可夫模型（HMM）。值得一提的是，隐马尔可夫模型（HMM）包含了双重随机过程：一是系统状态变化的过程，即前面所述的马尔可夫过程，另一个是由状态决定观察的随机过程。
举例：碗、球模型
    假设N只碗，每个碗中放着数量与比例均不同的各种色彩的球，不同的彩色球为M。先随机选一个碗，再从碗中随机拿一个球，报告球的颜色得到一个观察O_1，然后将球放回到碗中，继续这个过程，得到一系列观察O=O₁O₂O₃...O_T
    在这个模型中，碗（状态）是不可观察的，只有球的颜色是可观察的。这里引入M，指不同观察值的数目 。所有不同观察值记为V={V₁,V₂,....V_M}。
    对于第一种随机过程（选碗），时齐马尔可夫过程的转移概率矩阵：A={a_ij}，初始分布：π=(π_i)
    对于第二种随机过程，有多项分布B={b_j(k)}，其中
            b_j(k)=P[时刻t时观察值为V_k|q_t=S_j]
    给定一组N,M,A,B和π后，一个HMM即确定了，为紧缩起见，今后将用λ=（A,B,π）表示一个HMM。

3.HMM中三个基本问题
问题1：
    给定一个观察序列O=O₁O₂...O_T和一个模型λ=（A,B,π），如何有效计算P（O|λ），即给定模型λ的条件下，观察序列O的概率。
    问题1是一个计算概率的问题，也可以看成一个评估给定的模型能否很好地拟合给定的观察的问题。

解法：
（1）前向算法：
    定义α_t(i)=P(O₁O₂....O_t,q_t=S_i|λ)
    α_t可用递推算法完成计算：
    ①初始化：α₁(i)= π_ib_i(O₁)
    ②递推：
    ③终止：

（2）后向算法：
    定义β_t(i)=P(O_t+1,O_t+2,...,O_T|q_t=S_i,λ)
β_t可用递推算法计算：
    ①初始化：β_T(i)=1
    ②递推：
    ③终止：


问题2：
    给定一个观察序列O=O₁O₂...O_T和一个模型λ=(A,B,π)，如何选择一个相应状态Q=q₁q₂...q_T使得在某种意义下，它能最好地说明观察序列O。
两个准则：
准则1：对每个时刻t，逐个选取状态q_t使
    γ_t(i)=P(q_t=S_i|O,λ)=max
其中：

求出γ_t(i)后，问题2便迎刃而解。

准则2（应用最为广泛）：综合选取一个状态序列Q=q₁q₂....q_T使P(Q|O,λ)=max
    对于P(Q|O,λ)=P(Q,O|λ)/P(O|λ)
    而分母P(O|λ)与Q无关，因此等价于P（Q,O|λ）=max。
    对于全局最优问题，使用动态规划方法，这就是Viterbi算法。
    定义
            
    基于HMM特性，
            
    因为我们同样关心q₁q₂...q_T的序列，因此引入
            

    整个递推算法（Viterbi算法）描述如下：
    ①初始化
        δ₁(i)=π_ib_i(O₁)
        φ₁(i)=0
    ②递推
         
         
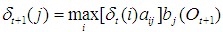
    ③终止
        
    ④回溯最佳路径
        q_t^*=φ_t+1(q_t+1^*)

    将其应用到词性自动标注中。在自动标注中，每个词是可观察的，一个词串W=w₁w₂....w_T即相当这里的一个观察序列O=O₁O₂...O_T。不可观察的状态相当于词性或概念标记，即状态序列Q=q₁q₂....q_T相当于上一节中的一个标记序列。
    可以看出准则1相当于词级评价，准则2相当于句子级评价。


问题3.
    如何修正模型参数λ=(A,B,π)使P(O| λ)=max。
    问题3是最困难的，至少也没有很好的解法。可参考的方法有基于均值修正的迭代方法等。

参考文献：
[1] 吴立德: 大规模中文文本处理[M]. 复旦大学出版社,1993.