(本文包括章节:1、由来,2、算法简单回顾,3、演习道具,4、演习,5、算法提出者Leslie的八卦。hoho)
1、由来:
刘备接受了诸葛亮的提议,决定将paxos算法的思想应用到蜀帝国的决策机制上。然而,玄德生性谨慎,决定先行试点,实践下可行性。孔明提议,由蜀国五大肌肉男:关羽、张飞、赵云、马超、黄忠,做为决策者,而廖化、周仓、魏延分别无序的提出关于同一件事的水火不容的三个提案,孔明坚信:即使脑残者使用了paxos算法,也不会出现冲突的政令不一情况。paxos算法理论以及刘备是怎么被孔明忽悠的部分,同学们可以参考上篇《paxos分布式一致性算法--讲述诸葛亮的反穿越》:http://blog.csdn.net/russell_tao/article/details/7244530
闲话少叙,书接上文。
为了少打点字,刘备与诸葛亮俩玻璃不再以对话形式出现了。他们设置了五个官署(五虎将办公地,相当于Server),三个提案点(周仓等三人,发起提案时的办公地。相当于Client),当然都不在一起,信使们从提案点到官署传递信息的话,正常情况下需要半个小时,也就是30分钟。这次演习,哥俩不关注学习情况,所以paxos第三段就不在演习内容里了。诸葛亮为廖化、周他、魏延对于事件e准备了三个自相矛盾的提案,我们分别用p1、p2和p3代替吧。先行说明提案:
事件e(也就是本次paxos实例):蜀国今后的发展路线
提案p1:学习红色锤子镰刀,走激进主义,一切发展按照计划进行,小民们凭票消费,银子多了也没用,集中力量办大事,崇尚国家垄断主义。
提案p2:学习自由联盟,走自由主义,宁失去效率也不失去公正,发展民营经济为先,民主、法制、新闻自由,通过这种公正来激发社会的整体创造力。
提案p3:坚持孔孟之道,走保守主义,兼顾黄老之学,坚信中学为体、西学为用,国体不可大改,走有大汉国情的老路让别人说去吧。
2、算法简单回顾
我们再简单回顾下提案者和作为决策者的五虎将行动准则,共有六步,书记官(暂让五虎将兼职)负责记录下通过的提案p(通过了就叫法令了),这样,我们用1a,1b,2a,2b,3a,3c来表述全部的六步。(这六步就是三段式提交了,这在上篇《paxos分布式一致性算法--讲述诸葛亮的反穿越》里讲过,不再复述。)
魏延、廖化、周仓:
1a,作为提案者,首先向刘备要到个编号,搞清楚自己对事件e的态度。记录下当前时间,接下来向五虎将的多数派(3个或以上)发送事件+编号。
2a,此时开始处理五虎将的回应,这就有多种情况了。收到明确拒绝就得放弃!检查沙漏,如果到达时间限制了,还没有足够的多数派回应,那么就试着给五虎将的其他人再发送提案看看。如果收到了足够的五虎将里多数派的回应,那么,确定在2a这步里,如果要提案,到底提哪个提议?是自己现在要提的提案?
3a,提案者如果收到足够的五虎将多数派回应通过,则记录提案为通过的政策法令,同时通知所有书记官,也就是兼职的五虎将,把法令记录到羊皮纸上来。
五虎将:
1b,作为决策者,也需要沙漏,主要用于2b步骤后批准政策法令后,给自己设定个超时时间,若第三步信使没有过来,则超时后自动把提案变成政策法令记录到羊皮纸上。1b这个步骤是收到了信使的消息,来自于1a步骤里的提案者。收到事件e和编号N。五虎将这时将有可能出现三个动作:拒绝、通过以及第三个复杂点的动作,虽然通过但告诉魏延廖化,哥曾经批准过某提案了。(三种条件的达成请参考上篇文章《paxos分布式一致性算法--讲述诸葛亮的反穿越》)
2b,与1b步骤相同,唯一不一样的是,如果决定批准某个提案,必须先把该提案和编号记录到羊皮纸的背面。(羊皮纸的详细用途参见演习前提)
3b,记录法案到羊皮纸的正面上。(本步骤不在下面演习中出现)
3、演习道具
先解释下我们用到的道具吧。
羊皮纸(相当于硬盘):其正面记录真正通过的法令,背面相当于永久有效的草纸,背面记录一个三元组(S,V,Sh),S表示上次批准的提案编号,V表示上次批准的提案,Sh表示处理过的最大提案编号。(羊皮纸丢掉后的效果在演习结束后说明)
草纸:与羊皮纸背面相同,记录三元组。唯一不同的是,草纸容易丢失。
沙漏:记录时间。我们简单的认为,任何两个地方一次通讯时间为30分钟。所以,如果我们从提案者那出发,信使到五虎将再回来,我们认为一个小时足矣(忽略五虎将或者提案者的处理时间)。
下面的演习中,只有消息的丢失,实际上对于消息的重发和延迟,也不会有任何问题。只是对五虎将的缺席,需要做说明。如果五虎将的羊皮纸丢失,是不能直接再次加入进五人决策团的,必须学习到最新的状态。没丢羊皮纸,则可以随时加入进来。
书记官记录法令中的不一致情况这里不加讨论。
为了方便在图表中表示,我们先给五虎将五个字母编号:关羽a,张飞b,赵云c,马超d,黄忠e。
三种颜色表示不同的提案者:黄色表示廖化,蓝色表示周仓,红色表示魏延。
下面这幅图,表示不同的时间点,五虎将和三个提案者当时的状态。
->表示第一步预提案。包括1a和1b两步。
-->表示第二步提交提案,包括2a和2b。
五虎将记录的(s,v,sh)表示的三元组上面讲过了。法令项下面对应的是提案者魏、廖、周三人的状态。(wait)表示刚发出提案,1小时内等待返回呢。
e is drop表示发送给e黄忠的提案消息丢失了。
好了,可以往下看了。
4、演习
先放图,解释在下面。
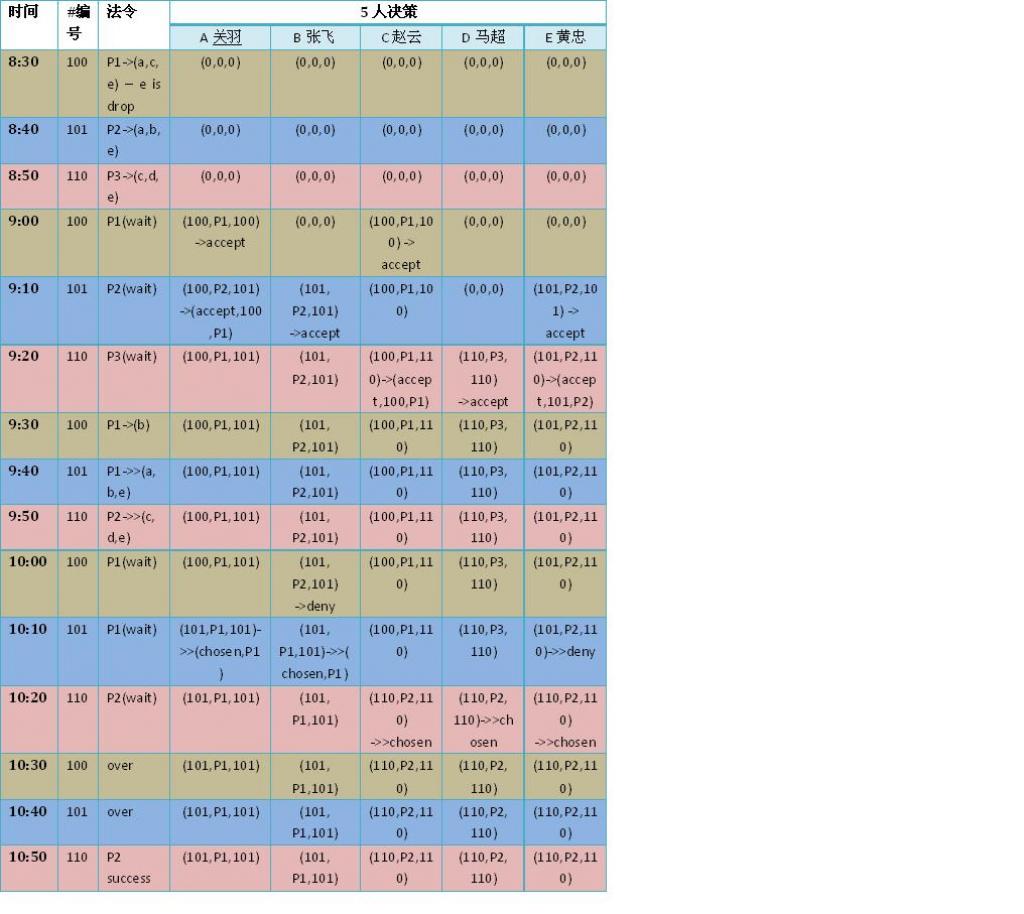
详细说明上图:
8:30分上班了,红色周仓同学首先向关羽、赵云、黄忠三人发出了提案p1,编号为100,周仓开始等返回,预计9:30分时能收到三位的返回。我们假定,发给黄忠的信使出门就被孔明的跑车撞了。孔明闯祸后老实了,以下,不再出现信使失误事件了。
8:40分,崇尚民主的廖化同学向关羽、张飞、黄忠三人发出了编号为101的提案p2,预计9:40分收到返回的信使。
8:50分,喜欢孔孟的魏延同学向赵云、马超、黄忠三人发出了编号为110(魏延就是搞到大编号了啊)的提案p3,预计9:50收到返回的信使。
9:00整,周仓的提案p1到了关羽、赵云手里(黄忠没收到),两人无条件接受,记录(100,p1,100),承诺编号低于100的提案我可不会再处理了,然后两个信使开始返回。
9:10分,廖化编号为101的提案p2到了关羽、张飞、黄忠之手,张飞、黄忠哥俩从没收过事件e的提案,毫无疑问记为(101,p2,101),让信使回复接受。关羽则不然,红脸兄在10分钟前收到了周仓的编号为100的p1提案。所以,按规则办,关羽改自己的记录为(100,p1,101),让信使给廖化回复:你的编号101比较大,我同意你继续,不过我之前同意过一个编号为100的提案p1,请注意哦。
9:20分,魏延的p3提案到了赵云、马超、黄忠三人之手,马超第一次收到提案,记为(110,p3,110),回复批准。赵云和黄忠则不同,赵云收到过周仓的p1提案,这时要比提案编号了,魏延的110大于周仓的100,于是赵云记为(100,p1,110),告诉信使:我通过了,我承诺编号小于110的我不会处理,同时,我曾经批准过编号为100的提案p1。同理,黄忠记为(101,p2,110),也告诉信使:我曾经批准过编号为101的提案p2。
9:30分,周仓同学检测返回的信使了,关羽和赵云都返回批准,但是黄忠没有返回。因为必须N/2+1,也就是大多数人批准才行,所以,周仓向张飞发出提案p1。
9:40分,廖化收到了来自关羽、张飞、黄忠的回复,三人皆表示同意,但关羽表示:关某曾收到过编号100的p1提案。所以按照规则,廖化此时不能坚持自己原来的提案p2,而要改成关羽返回的提案p1,然后发起提交皆段,同样是让信使带给关羽、张飞、黄忠三人,我们用->>(a,b,e)表示。
9:50分,魏延收到了赵云、马超、黄忠三人在9:20分的答复,三人都同意了,但回答各不相同。马超没有多话,赵云说我曾收到过编号为100的p1提案,黄忠说我曾经收到过编号为101的p2提案。于是,魏延根据规则,不再提自己原来的p3提案,改为101编号对应的提案p2。接着,魏延开始向这三人发出提交请求,编号为110的提案p2。
10:00整,张飞收到了9:30分周仓补发的编号为100的提案p1,这之前,张飞在9:10分时曾经批准过来自廖化的提案p2,编号是101。所以,张飞在9:10时就已经承诺了,以后决不再处理编号小于101的提案。于是,张飞大吼一声:我拒绝。当然信使将会在10:30才能把消息带给周仓。
10:10分,关羽、张飞、黄忠收到了来自廖化于9:40分发出的(101,p1)提案,关羽和张飞都发现自己可以批准,记录到羊皮纸的背面,同时告诉信使:告诉廖化P1提案我批准了,我承诺编号小于101的提案不予理会。黄忠则不然,老将黄忠在9:20分时收到过魏延编号为110的提案,那时他批准了,意味着,所有小于110的提案他都会拒绝掉。这次廖化的提案才101,当然被拒绝掉了。三人的回复将于10:40会到达廖化处。
10:20分,魏延编号为110的P2提案到达赵云、马超、黄忠,三人没有疑问,毕竟110编号最大,都表示批准,并记录(110,p2,110)到各自的羊皮纸背面,回复信使通过。
10:30分,周仓收到了他在9:30分发给张飞的回复,张飞在10:00拒绝了,所以周仓这个提案就此作废。
10:40分,廖化收到了10:10来自关羽、张飞、黄忠的回复,关张二人批准,然而老黄忠明确表示拒绝,于是这次编号101的提案作废。
10:50分,魏延收到了赵云、马超、黄忠的回复,三人都表示批准,于是编号为110的提案p2最终作为法令记录下来(之后的3b学习过程略过),从此以后,蜀国的路线被确立为走民主路线,许多年后,蜀国统一了银河系。完。
以上任何步骤,大家可以任意制造难度,例如让同一个信使重复投递消息,或者延迟一天后消息到达某虎将处。或者让某个虎将正常如厕,而后正常归来。大家会发现,一致性是可以达到的,无论怎样,对于同一个事件e,互相冲突的三个法案:p1,p1,p3,一定只有一个可以达成。
对于任一虎将兄的挂掉,我们要分情况。如果是去大便,那么他的羊皮纸是不能丢的。大便完了,可以正常回到自己的官署办公。但是如果把羊皮纸丢了,那就不能立刻加入,必须向所有其他人学习,把失落的过程都学到,才能正常加入。这点至关重要,就是说,只要硬盘不坏,随时SERVER重启都能加入。硬盘一坏,对不起,学习完了才能继续办公。
5、后记---Leslie的八卦:
paxos算法是解决分布式服务数据一致性的终极算法,google的基础服务chubby(GFS的基础服务)的开发者说, “there is only one consensus(一致性) protocol, and that’s Paxos”。Microsoft有fast paxos论文,yahoo的zookeeper也用了paxos算法。可见,paxos是解决完全的分布式服务(无单点)间数据一致性的最好方法。但是paxos比较复杂,特别是网上的中文资料里少有能说得清楚的(主要是太多paxos变种算法了,掺合到一起搅得人头大),例如中文wiki上的paxos解释,光看这个是不可能搞懂paxos的。
paxos算法由Leslie Lamport在1990年提出,毫无疑问,paxos想解决的就是分布式环境下(server会挂掉,通讯协议不可靠,消息可能延迟、丢失、重发)如何保持数据一致性的问题。Leslie Lamport同学在1982年提出的“拜占庭将军”问题上尝到了甜头,这也是个分布式环境下的一致性问题,Leslie通过类比的方式,伪造了“拜占庭将军”历史,通过这种简单的类比成功的简化了复杂的分布式环境,效果非常好。于是在1990年Leslie同样用类比的方式提出了paxos算法,该问题跟“拜占庭将军”问题的区别是,“拜占庭将军”允许有叛徒,也就是允许伪造消息(默许被黑客攻击),而paxos则不允许消息被伪造。
Leslie很有幽默感的把论文写成一个考古发现,至始至终都在虚构他的“考古发现”。他说在考古中发现了失落的文明:希腊的paxos小岛。这里的议员通过邮递员传递消息,议会中一个议员提出法案,多数议员批准后法案获得通过。当然无论议员还是邮递员,都是兼职的,他们不可靠,随时可能走人,呵,典型的分布式环境,server可以挂,消息可以丢。Leslie根据考古文献反推出了paxos议会如何搞定法案一致性的问题。
发表论文时,Leslie一直用这种语气在写论文,于是《ACM Transactions on Computer Systems》编辑们认为太荒诞了,不能从头到尾虚构故事吧?毕竟是严谨的科学杂志,于是打回。Leslie同学身为牛人,坚持自己的看法,同时认为编辑们没有幽默感,拒绝修改。时间流逝,一晃九年过去,九年后有团队根据该论文开发出一个paxos实现,终于,编辑们低头了,允许发布Leslie的论文,但还是加了段编者著,在其中表示Leslie其实是个热爱计算机技术的考古学家!也算稍事解嘲。
写这两篇文章,我也试了下借喻的手段,用我们熟悉的三国人物,看看能否讲清楚paxos。其实paxos的算法本身算不得很复杂,但如果想讲清楚在各种异常情形下paxos算法的表现,给大家带来的明确的直观感受:paxos确实能解决一致性问题,这就不容易了。所以篇幅所限,只写了丢失一个消息的情况。不过大家如果从头看到这,应该可以简单的任意推导出其他异常吧?
最后,上面说的只是算法机制,如果需要了解现有的各种产品实现,最方便的还是看zookeeper源码,毕竟是开源的,例如去:http://zookeeper.apache.org/doc/r3.3.2/zookeeperOver.html,可以看下概述。淘宝开发团队有许多关于zookeeper实现的文章,到网上搜下就能看到。
对google的chubby实现,因为不是开源的,只有篇论文可以看:http://static.googleusercontent.com/external_content/untrusted_dlcp/research.google.com/zh-CN/us/archive/chubby-osdi06.pdf