如何理解预测技术呢?简单来说,预测(prediction)是根据事物发展的历史资料及当前情况,运用一定的理论和方法,对未来趋势做出的一种科学推测。再简单点,就像传说中或是童话里的占卜师一样,当你想知道将来的事情时,你需要告诉占卜师你的出生情况,他就能将你的一生预测出来。不同的是,他只能告诉你,你的一生是顺利或是不顺,或再详细点告诉你可能在哪段时间会发生不寻常的事情;而我们所说的预测技术却可以详细到周,甚至详细到天。当然,这里还有个本质的区别,那就是我们这里说的预测是有科学基础的,而占卜师的预测只是常常出现在童话里或者传说中罢了。
预测技术的应用主要针对未来的趋势,即是经常讲的趋势预测?这里我们也来个“顾名思义”。“趋势”一词在词典里的解释是“事物发展的动向”,也就是会呈现出某种规律。简单点,某一事物未来是好是坏,是多是少,是升是降,或者先好后坏,先多后少,先升后降等等,也就是对未来进行预测。再用上面的例子来说明,小李急切地想知道自己的未来,并求助于占卜师,而占卜师则预测到他在40岁时会有场灾祸,那么恐怕小李紧接着要问的就是“我该怎样做才能化解我的灾祸”。趋势预测就是要解决类似的问题。预测并不是最终目的,而是一种手段,当预测到的趋势不符合规定的标准时,就应当及时采取措施来进行调整或缓解,这也是趋势预测的目标之一,通过分析预测的结果,揭发它的发展趋势,从而使得人们能够尽早地发现问题,或得到一个科学论断和标准。现在从童话回到现实中来。在软件领域,缺陷的趋势预测是预测技术应用较为广泛的领域之一,它是利用统计的手段来预测产品或解决方案中的遗留缺陷、测试阶段的单位时间内应当查出的缺陷等,因此对软件质量的提高和测试阶段的管理起着重要作用。
成长曲线
终于要介绍到预测方法啦。有了前面两篇文章的基础,大家应该都对预测有了认识。还是那句话,知道了要做什么,接下来就该想要“怎么做”。明白了预测的重要性,那就该去想想,怎么去预测?不过别心急,我们一步一步来,这篇文章会介绍预测工具的基础知识——成长曲线。
什么是成长曲线?成长曲线就是描绘观测样本从初始阶段不断发展壮大所经历的全部过程的曲线。在软件领域的成长曲线的过程中,要观测的样本值会经历萌芽、发展、稳定等阶段。成长曲线在很多方面都有应用,比如在报纸上、经济类刊物上常常能看到的经济成长曲线、品牌成长曲线;再比如细心的妈妈都会把宝宝出生后的成长情况记录下来,绘成儿童成长曲线等等。
在软件领域中同样有成长曲线,软件领域中的成长曲线反映了软件系统中的要观测的某个属性随着各种因素(如时间、成本等)变化发展的情况。成长曲线可以拟合事物发展的趋势,曲线拟合(Curve fitting)就是用连续曲线近似地刻画或比拟平面上离散的点表示的坐标之间的函数关系的一种数据处理方法。在数值分析中,曲线拟合就是用解析表达式逼近离散数据,即离散数据的公式化,就是选择适当的曲线类型来拟合观测数据,并用拟合的曲线方程分析两变量间的关系。
接着回到软件领域中的成长曲线上。对于一个系统来说,进入开发阶段后,开发人员每天都要完成一定量的代码行,而代码行的总数在项目计划阶段就应当是估算好的,那么,开发人员应当按照怎样的速度完成这些代码;已经完成了一部分代码后,能否判断出这样的速度是否合理、能否按期完成任务;前期完成过多代码可能会造成后期工作量太小,而前期完成太少代码又可能会带来后期的工作繁重。也许这时,你就会迫切需要一个工具来对开发人员的工作进行监控。进入测试阶段也是一样。所以这里提到的软件领域中的成长曲线的预测,就是针对软件的开发阶段和测试阶段的。再以测试为例,成长曲线能够反映缺陷从最初的测试出的缺陷较少,到中期不断发展增多,再到最终测出的缺陷数稳定不变的全部过程。成长曲线应当是连续的,它能够表示一段时间内事物持续发展的情况,能够表示事物在一个持续的时间段内发展的全过程。
成长曲线有很多种形式。常见的线性曲线也可以看作是成长曲线的一种,只是在现实中,线性曲线的使用不如非线性曲线广泛。下面将几种常见的成长曲线归纳介绍,希望对大家的理解有所帮助。
1、Rayleigh模型
Rayleigh模型是Weibull分布的一种特殊形式,是一种常用的模型。Weibull分布最重要的一个特征是它的概率密度函数的尾部逐渐逼近0,但永远达不到0,在许多工程领域都使用了很多年。Rayleigh模型既可以对软件开发全生命周期进行预测,也可以仅对测试阶段的缺陷分布进行预测,得到所期望的时间间隔t与所发现缺陷的关系。对于成熟的组织,当项目周期、软件规模和缺陷密度已经确定时,就可以得到确定的缺陷分布曲线,并可以据此控制项目过程的缺陷率。如果项目进行中实际的缺陷值与预估的缺陷值有较大差别时,说明中间出现问题,需要加以控制。
1)Rayleigh模型的函数形式
Rayleigh模型的累积分布函数(CDF):F(t)=K*(1-exp^(-(t/c)^2));
Rayleigh模型的概率密度函数(PDF):f(t)=2*K*t/(c^2)*( exp^(-(t/c)^2))。
上面两个函数中,t是时间自变量,c是一个常量(c=2^(1/2)tm,tm是f(t)到达峰值对应的时间),K是曲线与坐标形成的面积(总缺陷数),也是我们要估计的参数。多年的预测经验得到缺陷在tm时间的比率(F(tm)/K)约等于0.4,即在f(t)到达最大值时,已出现的缺陷大约占总缺陷的40%。按照这个推导,在某一时间就可以估算出总的缺陷数以及具体的Rayleigh分布参数,从而将缺陷的计算过程简化。
2)Rayleigh函数对应的图
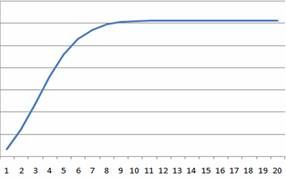
图1 Rayleigh模型的CDF图

图2 Rayleigh模型的PDF图
由图1——CDF图可以看出,累积密度最终趋近一个最大值(K);由图2——PDF图可以看出,缺陷随时间逐渐降低最终趋向于0。
)使用Rayleigh曲线来建模软件开发质量涉及两个假设:
在开发过程中观察到的缺陷率与应用中的缺陷率成正比关系。对应于图1来说,也就是如果开发过程中观测到的缺陷率越高,CDF中图的幅度越高,K值越大;
给定同样的错误植入率,假如更多的缺陷被发现并更早将其移出,那么在后期阶段遗留的缺陷就更少,应用领域的质量就更好。对应于图2来说,曲线与X、Y轴围成区域的面积是一定的(总的缺陷数是确定的),如果在前期移除较多缺陷,即曲线的峰值点前移,那么后期曲线的面积就会小,代表后期遗留的缺陷数减少。
4)使用场景:收集数据应当越早越好;且需要持续的追踪缺陷数。
5)优势:随时间信息的缺陷密度可预测,因此在测试阶段使得找到并验证缺陷的估计成为可能。
6)Rayleigh模型没有考虑到变化调整的机制,所以可能会影响到缺陷的预测。
2、指数模型
指数模型是针对测试阶段,尤其是验收类测试阶段的缺陷分布的模型,其基本原理是在这个阶段出现的缺陷(或者失效模式,我们这里讨论的是缺陷)是整个产品可靠性的良好指证。它是Weibull系列的另一个特例。指数模型是许多其他可靠性增长模型的基础。指数模型可分为故障/失效计数模型(fault/failure count model)和失效间隔时间模型(time between failures model)。基本的指数模型的累积缺陷分布函数(CDF)为y=K*a*b^t,修正指数模型在基本指数模型曲线函数上加一个常数因子。
1)指数模型的函数形式
指数模型的累积缺陷分布函数(CDF):F(t)=K*(1-exp(-λ*t));
指数模型的缺陷概率密度函数(PDF):f(t)=K*(λ*exp(-λ*t))。
其中,t是时间,K是总缺陷数,λ与K是需要估计的两个参数。
2)指数模型对应的函数图
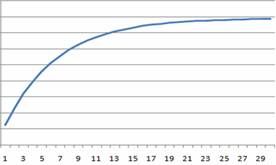
图3 指数模型的CDF图

图4 指数模型的PDF图
2)指数模型的关键假设:测试工作量在测试阶段中是均匀的。
3)使用:指数模型预测缺陷时是基于正式的测试阶段的数据的,因此它主要适用于这些阶段,最好在开发过程后期——例如最后的测试阶段。但在交付用户使用后,用户发现的缺陷模型,与交付用户之前的模型往往有很大差别,这是由于交付客户后影响客户的测试的不确定因素更多。
4)优势:最简单最有用的模型之一,易于使用和实现。
5)缺陷:假设测试的工作量在整个测试阶段是均匀的。
3、NHPP模型(非齐次泊松过程模型)
NHPP模型是对在给定间隔内观察到的故障数建模,它是指数模型的一个直接应用。
1)NHPP模型的函数形式:其中,参数的含义与指数模型相同
NHPP模型的累积缺陷分布函数(CDF):F(t)=K*(1-exp(-λ*t));
NHPP模型的缺陷概率密度函数(PDF):f(t)=K*λ*c^(-λ*t)。
2)NHPP模型对应的函数图:见指数模型
3)由于NHPP模型是指数模型的应用,所以NHPP 模型的特征与指数模型的特征相同。
4)缺陷:大多数NHPP模型都基于这样的假设:每个缺陷的严重性和被监测到的可能性相同,在排除一个缺陷时不引入另一个新的缺陷,但实际情况并非如此。缺陷之间是存在着关联关系的。
4、S型可靠性增长模型
S型增长模型是软件领域应用较为广泛的模型之一,下一篇,将会详细进行介绍。
未完待续。。。