一、正交表的由来
1、拉丁方名称的由来
古希腊是一个多民族的国家,国王在检阅臣民时要求每个方队中每行有一个民族代表,每列也要有一个民族的代表。
数学家在设计方阵时,以每一个拉丁字母表示一个民族,所以设计的方阵称为拉丁方。
2、什么是n阶拉丁方?
用n个不同的拉丁字母排成一个n阶方阵(n<26 ),如果每行的n个字母均不相同,每列的n个字母均不相同,则称这种方阵为n*n拉丁方或n阶拉丁方。每个字母在任一行、任一列中只出现一次。
3、什么是正交拉丁方?
设有两个n阶的拉丁方,如果将它们叠合在一起,恰好出现n2个不同的有序数对,则称为这两个拉丁方为互相正交的拉丁方,简称正交拉丁方。
例如:3阶拉丁方
A B C A B C
B C A 和 C A B
C A B B C A
用数字替代拉丁字母:
1 2 3 1 2 3 (1,1)(2,2)(3,3)
2 3 1 和 3 1 2 ---> (2,3)(3,1)(1,2)
3 1 2 2 3 1 (3,2)(1,3)(2,1)
二、正交试验法介绍
人类在认识自然界的过程中,进行着多方面的探索,试验是构成学习过程的一个重要要素。
爱迪生一生艰苦奋斗,经历了无数次的失败之后,为人类发明了许多重要的科技成果。他的座右铭是:“天才靠的是百分之一的灵感和百分之九十九的汗水”。他的助手在他去世后的第二天说:“如果在爱迪生工作的黑屋中能有一支蜡烛照亮他前进的方向,以他蜜蜂般地努力,他会获得远比他发明多的多的成果”。就是说如果有一点理论知识和计算能帮助爱迪生,他会节省90%的精力。爱迪生是边试验边分析后决定下次试验,这种方法速度太慢。
正交试验设计是研究多因子(术语解释:把实验中影响响应变量的那些变量称为实验中的因子,因子分为可控因子和非可控因子)多水平(术语解释:把因子不同的取值称为水平)的一种试验方法,它是根据正交性从全面试验中挑选出有代表性的点进行试验,正交试验具备了“均匀分散,齐整可比”的特点,正交试验设计是分式析因设计的主要方法。
日本著名的统计学家田口玄一将正交试验选择的水平组合列成表格,称为正交表。例如作一个三因素三水平的实验,按全面实验要求,须进行33=27种组合的实验,且尚未考虑每一组合的重复数。若按L9(33) 正交表安排实验,只需作9次,大大减少了工作量。正交实验设计是一种高效率、快速经济的实验设计方法,因此在很多领域得到广泛应用。
利用场景法来设计测试用例时, 作为输入条件的场景非常庞大,以至于得到的测试用例数目多的惊人,给软件测试带来沉重的负担。如果舍弃一些场景又怕测试设计的覆盖度达不到,将缺陷遗留给客户。为了有效地减少测试缺陷遗留,合理地减少测试的工时与费用,从2008年开始公司推行正交试验设计方法进行测试用例的设计。
三、正交表的构成
1、正交表的构成
行数(Runs):正交表中的行的个数,即试验的次数,也是我们通过正交实验法设计的测试用例的个数。
因子数(Factors) :正交表中列的个数,即我们要测试的功能点。
水平数(Levels):任何单个因子能够取得的值的最大个数。正交表中的包含的值为从0到数“水平数-1”或从1到“水平数” 。即要测试功能点的输入条件。
2、正交表的形式
L行数(水平数因子数)
如:L8(27)
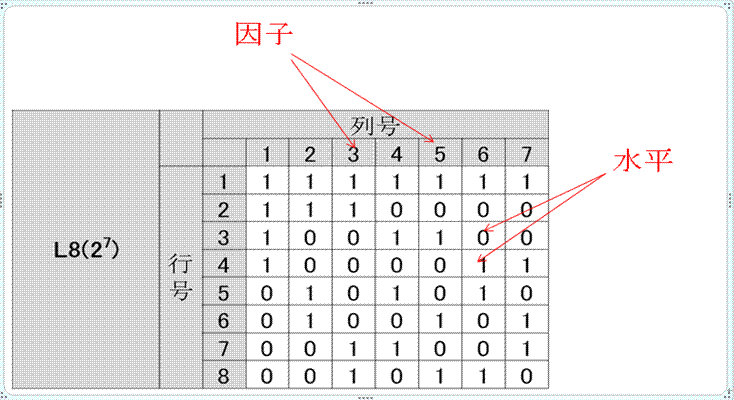
3、正交表的正交性
● 整齐可比性
在同一张正交表中,每个因子的每个水平出现的次数是完全相同的。由于在试验中每个因子的每个水平与其它因子的每个水平参与试验的机率是完全相同的,这就保证在各个水平中最大程度的排除了其它因子水平的干扰。因而,能最有效地进行比较,容易找到较佳的试验条件。
● 均衡分散性
在同一张正交表中,任意两列(两个因子)的水平搭配(横向形成的数字对)是完全相同的。这样就保证了试验条件均衡地分散在因子水平的完全组合之中,因而具有很强的代表性,容易得到好的试验条件。
4、用正交表设计测试用例的优点
● 不需要对所有组合情况穷举,只需要少量的抽样组合数据,可明显地提高效率;
● 用正交表抽样出的组合数据,对组合情况具有最佳的覆盖性;
● 能减少手工对组合数据抽样导致的大量测试遗漏
四、设计步骤
(1)提取功能说明,提取因子
把影响实验指标的条件称为因子,而影响实验因子的条件叫因子的水平。
利用正交实验设计方法来设计测试用例时,首先要根据被测试软件的规格说明书找出影响其功能实现的操作对象和外部因素,把它们当作因子;而把各个因子的取值当作状态,把它们当做水平。对软件需求规格说明中的功能要求进行划分,把整体的、概要性的功能要求进行层层分解与展开,分解成具体的有相对独立性的、基本的功能要求。这样就可以把被测试软件中所有的因子都确定下来,并为确定每个因子的权值提供参考的依据。确定因子与状态是设计测试用例的关键。因此要求尽可能全面的、正确的确定取值,以确保测试用例的设计作到完整与有效。
(2)判断是否可以使用正交表
并不是任何情况都可以使用正交表,以下情况无法使用正交表:
● 因素的个数非常少,如只有2个;
● 因子数很大。
另外在识别的因子中,还要进行以下分析:
● 组合因素之间必须为平行关系(平行:可以同时存在)
● 不能为互斥(互斥:1个因素存在,另1个因素不能存在)
● 因素不能被其它因素的因子制约(制约:当A因素的因子为A1,B因素不能存在)
● 排除非组合因素
(3)查找和调整正交表
如果判断可以使用正交测试方法设计测试用列,需要根据测试功能点的实际情况,选择正交表。
选择正交表的原则如下:
● 实际因素数≤正交表因素数;
● 实际每个因子数≤正交表每个因子数;
● 如果出现2个或2个以上正交表符合以上条件,则选择Case数最少的正交表。
选取了正交表后,删除正交表中多余的因子列,原则是删除靠后的列;
(4)加权筛选,生成因素分析表
对因子与状态的选择可按其重要程度分别加权。可根据各个因子及状态的作用大小、出现频率的大小以及测试的需要,确定权重的大小。对于权重高的因子放在最前面的列中,以此类推。
(5)把变量的值映射到表中
在使用正交法时,要考虑到被测系统中要准备测试的功能点,而这些功能点就是要获取的因子,但每个功能点要输入的数据按等价类划分有多个,也就是每个因素的输入条件,即状态或水平值。
选取了因子和水平后,需要把变量实际的值映射到正交表中。
(6)正交测试用例的制作
把实际因子和水平代入正交表后,每一行制作成一个测试用例。
(7)组合补充测试用例
根据需求规格说明书或错误推断法,补充需要测试但正交表没有覆盖的测试数据,将其制作成测试用例。