∪∩deniable Design

个人JAVA版GAE(google app engine),struts2+jpa+jQuery开发,互相交流 http://iunbug.appspot.com/
  BlogJava :: 首页 :: 新随笔 :: 联系 :: 聚合  :: 管理

Visual C++ 6.0调试功能 图解教程(4)--实例三

Posted on 2008-08-19 17:37 ∪∩BUG 阅读(1224) 评论(0)  编辑  收藏 所属分类: VC++/MFC学习笔记

图

 

  1. 实验目的

    熟悉图的两种常用的存储结构，以及在这两种存储结构上的两种遍历图的方法，即深

    度优先遍历和广度优先遍历。进一步掌握递归算法的设计方法。

    关于各种典型著名的复杂算法，在上机实习方面不做基本要求。更适合于安排大型课

    程设计。

二.需求分析

    本程序演示用C++编写,完成有向图的创建,用Prim算法实现最小生成树,实现边的插入和删除.

输入值的范围:创建图时要求输入的结点个数不大于MaxVertices的值.在插入边时要求原图不存在起点和终点之间边,并且插入的边不是矩阵对角线上的边.输入的数据类型为整形.

输出形式:以邻接矩阵的形式输出图的数据项.如果操作非法则给出错误信息.

测试数据

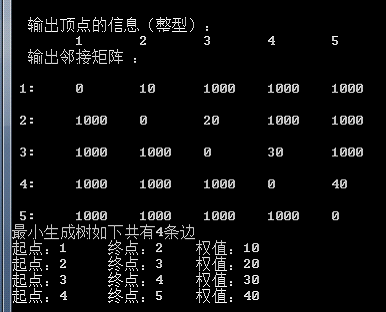
A创建5个顶点4条边的图:输入顶点分别为1,2,3,4,5;1和2之间,2和3之间,3和4 之间,4和5之间的权值分别为10,20,30,40.得到图:

输出顶点的信息（整型）：

1 2 3 4 5

输出邻接矩阵 ：

 

1: 0 10 1000 1000 1000

 

2: 1000 0 20 1000 1000

 

3: 1000 1000 0 30 1000

 

4: 1000 1000 1000 0 40

 

5: 1000 1000 1000 1000 0

B顶点4和3之间插入一条权值为50边得

输出顶点的信息（整型）：

1 2 3 4 5

输出邻接矩阵 ：

 

1: 0 10 1000 1000 1000

 

2: 1000 0 20 1000 1000

 

3: 1000 1000 0 30 1000

 

4: 1000 1000 50 0 40

 

5: 1000 1000 1000 1000 0

 

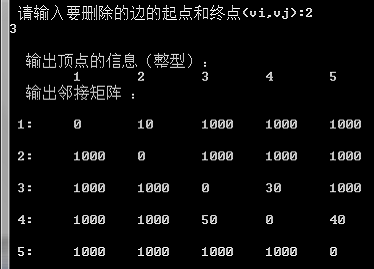
C删除顶点4和3之间的边得

 

输出顶点的信息（整型）：

1 2 3 4 5

输出邻接矩阵 ：

 

1: 0 10 1000 1000 1000

 

2: 1000 0 20 1000 1000

 

3: 1000 1000 0 30 1000

 

4: 1000 1000 1000 0 40

 

5: 1000 1000 1000 1000 0

三.设计概要

(1)为了实现上述程序的功能,需要定义图的抽象数据类型:

ADT Graph is{

数据对象：D={ai|ai∈IntegerSet,i=0,1,2,…,n,n≥0}

基本操作:

CreatG()

操作结果:创建有向图

InsertE()

初始条件:有向图已经存在

操作结果:插入一条边

DeleteE ()

初始条件: 有向图已经存在

操作结果:删除一条边

}END ADT BiTree

(2) 本程序包含一个类和一个结构体类型

A无向图类AdjMWGraph有7个函数

    1主函数                                main()

    2.构造函数                            AdjMWGraph()

    3. 创建图函数                            CreatG(int n,int e)

    4. 插入边函数                            InsertE()

    5. 删除边函数                            DeleteE()

    6. 求最小生成树Prim算法函数                Prim()

B结构体类型MinSpanTree

(3)本程序的两个文件

1.头文件    Graph.h

2.源文件     Graph.cpp

(4)函数之间的关系

 

 

四.详细设计

  1//Graph.h
  2#include "iostream"
  3#include <iomanip>
  4#include <stdlib.h>
  5using namespace std;
  6const int MaxVertices=10;
  7const int MaxWeight=1000;
  8struct MinSpanTree                            //带权边的三个参数
  9{ 
 10        int begin,end;                        //边的起点与终点
 11        int length;                            //边的权值
 12};
 13
 14class  AdjMWGraph
 15{ 
 16private:
 17      int  Vertices[20];                        //顶点信息的数组
 18      int  Edge[MaxVertices][MaxVertices];        //边的权信息的矩阵
 19      int  numE;                            //当前的边数
 20      int  numV;                            //当前的顶点数
 21public:
 22     AdjMWGraph();                              //构造函数
 23     void  CreatG(int n,int e);                    //创建图函数
 24     void  PrintOut();                            //打印图中数据项函数
 25     void  Prim() ;                                //求最小生成树方法(Prim算法)
 26     void InsertE();                                //插入边函数
 27     void DeleteE();                             //删除边函数
 28};
 29//Graph.cpp
 30#include "Graph.h"
 31
 32//初始化矩阵
 33AdjMWGraph::AdjMWGraph()                            //构造函数
 34{    
 35    //初始化矩阵为
 36    for ( int i = 0; i < MaxVertices;  i++ )                //行
 37      for ( int j = 0;  j < MaxVertices;  j++ )                //列
 38          { 
 39            if( i==j )  
 40                Edge[i][j] = 0;                        //对角线置零
 41            else   
 42                Edge[i][j] = MaxWeight;                 //无边时权值置这无穷大
 43        }
 44  numE = 0;                                         //当前边个数初始为
 45  numV = 0;                                         //当前的顶点个数为
 46}
 47
 48//创建图
 49void  AdjMWGraph::CreatG(int n,int e)
 50{
 51    int vi,vj,w;
 52     numE = e;  
 53     numV = n;
 54    cout<<"\n  输入顶点的信息（整型）：" ;
 55
 56    //顶点赋值
 57    for (int i = 0; i < numV; i++ )
 58    { 
 59        cout<<"\n "<<i+1<<": ";
 60        cin >> Vertices[i];
 61
 62    }
 63
 64    //边赋权值
 65    for ( int i = 0; i < numE;)
 66    { 
 67        cout<<"\n  输入边的信息（vi,vj,W）：";
 68        cin >> vi >> vj >> w;
 69
 70//判断起点和终点是否存在,是否是对角线上的点并且边是否存在
 71        if ((vi != vj ) 
 72            && (vi>0 && vi<=numV)
 73            && (vj>0 && vj<=numV)
 74            &&  (Edge[vi-1][vj-1] == MaxWeight))    
 75         {
 76                 Edge[vi-1][vj-1] = w;            //更改对应的行和列的权值
 77                 i++;
 78        }
 79         else
 80         {
 81             cout << "\t插入位置错误或边已经存在!\n\t请正确输入." <<endl;
 82         }
 83    }
 84 }
 85
 86//打印图中数据项
 87void AdjMWGraph::PrintOut()
 88{ 
 89    cout << "\n  输出顶点的信息（整型）：\n";
 90    for ( int i = 0; i < numV;  i++ )
 91        cout << "\t" << Vertices[i] ;
 92    cout << "\n  输出邻接矩阵：" <<endl;
 93    for ( int i = 0; i < numV; i++ )
 94       {
 95           cout << "\n "<< i+1 <<": ";
 96           for ( int j = 0; j < numV ; j++ )
 97              cout << "\t" << Edge[i][j] ;
 98           cout << endl;
 99       }
100 }
101
102//Prim普里姆算法求最小生成树
103void  AdjMWGraph::Prim ()
104{ 
105    int  n = numV,m,v;                                //顶点总数
106   MinSpanTree e, mintree[MaxVertices];                    // mintree 生成树数组
107
108   for (int j = 1; j < n;  j++)                            //初始化tree[n-1]
109     {    
110         mintree[j-1].begin = 1;                        //顶点并入U
111         mintree[j-1].end = j+1;                        
112         mintree[j-1].length = Edge[0][j];                // G.Edge[][]是连通网的带权邻接矩阵
113    }
114
115  for (int k = 0; k < n-1; k++)                            // 求第k+1条边
116   {
117       int min = MaxWeight;                            
118
119      for (int j = k; j < n-1;  j++)
120         if (mintree[j].length < min )                    //求邻接的最小的边
121         {
122             min = mintree[j].length;  
123             m = j;
124         } //for j
125
126     //交换方法置下个邻接点为终点
127      e = mintree[m]; 
128      mintree[m] = mintree[k]; 
129      mintree[k] = e;
130      v = mintree[k].end;                             //V∈U
131
132       for (int j = k+1;  j < n-1;  j++)                    //在新的顶点v并入U之后更新tree[n-1]
133      {
134          int d = Edge[v-1][mintree[j].end-1];
135          if (d < mintree[j].length)                    //循环找到与当前点相邻的最小权值的边
136          {  
137              mintree[j].length = d;                    
138              mintree[j].begin = v;                    //置当前点为起点
139          }
140     }// for k
141  }
142     for (int j = 0;j < n-1;  j++)
143        cout<<"\n"<<"起点："<< mintree[j].begin <<"     终点："<<
144                    mintree[j].end<<"    权值："<<mintree[j].length;
145     cout << endl;
146}
147
148//插入一条的算法
149void AdjMWGraph::InsertE()
150{
151        int i,j,w;
152         cout << "\n 请输入插入边的起点,终点和权值(vi,vj,W):";
153         cin >> i >> j >> w;
154         //判断起点各终点是否存在并且不是对角线上的点
155         if ( ( i != j ) && (i>0 && i<=numV) && (j>0 && j<=numV))        
156         {
157             if ( (Edge[i-1][j-1] != 0) && (Edge[i-1][j-1] == MaxWeight) )
158             {
159                 Edge[i-1][j-1] = w;        //更改对应的行和列的权值
160             }
161             else 
162             {
163                 cout << "\t边已经存在!" << endl;
164                 //exit (0);
165             }
166         }
167         else
168         {
169             cout << "\t插入位置错误!" <<endl;
170             //exit (0);
171         }
172
173}
174
175//删除一条边的算法
176void AdjMWGraph::DeleteE()
177{
178        int i,j;
179         cout << "\n 请输入要删除的边的起点和终点(vi,vj):";
180         cin >> i >> j;
181         if ((i>0 && i<=numV) && (j>0 && j<=numV))        //判断起点各终点是否存在
182         {
183//判断是否是对角线上的点,判断是否是边已经存在
184            if(( i != j ) && (Edge[i-1][j-1] != MaxWeight) )        
185                {
186                    Edge[i-1][j-1] = MaxWeight;            //对应的行和列权值置零
187
188                 }
189            else 
190            {
191                cout << "\t删除的边不存在!" << endl;
192                //exit (0);
193
194            }
195         }
196         else
197         {
198             cout << "\t删除位置错误!" <<endl;
199             //exit (0);
200         }
201
202}
203
204int main(int argc, char* argv[])
205{ 
206     AdjMWGraph  G ;  
207     int n,e;
208     int k;
209
210     do
211     {
212         cout << "\n\t 1.创建图" <<endl;
213         cout << "\n\t 2.插入一条边" <<endl;
214         cout << "\n\t 3.删除一条边" <<endl;
215         cout << "\n\t 4.退出" <<endl;
216         cout << "\n\t ==========================" << endl;
217         cout<<  "\n\t请输入您的选择(1,2,3,4):"; 
218         cin >> k;
219
220         switch(k)
221         {
222
223         case 1:
224             {
225                cout << "\n  请输入图的总顶点数和总边数（n,e=?）："; 
226                cin >> n >> e ; 
227                G.CreatG(n,e); 
228                G.PrintOut();        
229                cout << "最小生成树如下";
230                cout << "共有" << n-1 << "条边" ;        
231                G.Prim();  
232             }break;
233
234         case 2:
235             {
236                 G.InsertE();
237                 G.PrintOut();    
238                 G.Prim(); 
239
240             }break;
241
242         case 3:
243             {
244                 G.DeleteE();
245                 G.PrintOut();
246                 G.Prim(); 
247
248             }break;
249         case 4:
250             exit (0);
251         }
252     }while( k >0 && k <5 );
253     return 0;
254}
255


五.心得:

    这次实验我把无向图改成有向图后,对实验中给出的生成最小生成树的Prim算法感到费解这里只能说说在实现插入和删除时的心得.在创建图时我在程序中加入判断语句,因为在给边权时如果顶点不存在会造成锁死,严重影响调试.在创建和插入中主要判断的是:1,顶点是否越界.2边是否已经存在.3插入位置是否是矩阵的对角线.在删除中判断1,顶点是否越界.2边是否已经存在.对于Prim算法的求最小生成树的思想能够理解,但对于算法的实现不甚理解.希望老师在下次实验时讲解.

六.使用说明

    程序名为No5.exe运行环境为DOS,执行后显示:

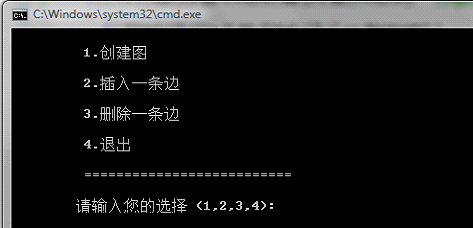
在" 请输入您的选择(1,2,3,4):"后输入数字选择执行的功能.

测试结果:

  1. 选择1.输入如图:

得

  1. 选择2操作如图:

再次操作

再次操作

3)选择3操作如图

再次操作

再次操作

4) 选择4或输入非"1,2,3"的数字

七.调试过程

    本程序主要对插入边操作功能进行调试..

  1. 将光标移置Graph.cpp文件的void AdjMWGraph::InsertE()的第一条语句处Ctrl+F10开始单步调试
  2. 选择1.后创建图

再选择2.

  1. 这时Debugger仍停留在void AdjMWGraph::InsertE()的第一条语句上.在中输入numV, I, j ,i!=j ,Edge[i-1][j-1]进行观察.F10单步至cin >> i >> j >> w;语句.然后在DOS窗口输入4,3,55回车.

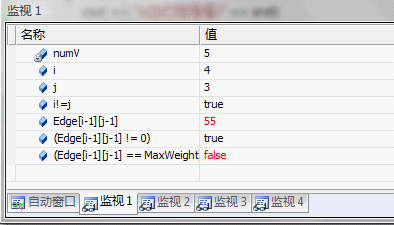
    这时Debugger仍停留在if ( ( i != j ) && (i>0 && i<=numV) && (j>0 && j<=numV))处.可以在监视1窗口中看到 i != j的值为true,即可以步入if()语句.

  2. 在监视窗口1中输入: (Edge[i-1][j-1] == MaxWeight), (Edge[i-1][j-1] != 0)进行观察,F10单步调试,这时Debugger停留在if ( (Edge[i-1][j-1] != 0) && (Edge[i-1][j-1] == MaxWeight) )语句处,同时在监视窗口1中可以看到(Edge[i-1][j-1] == MaxWeight), (Edge[i-1][j-1] != 0)都为真,即可以步入if()语句中.F10后可以看到Edge[i-1][j-1]值已经变为55

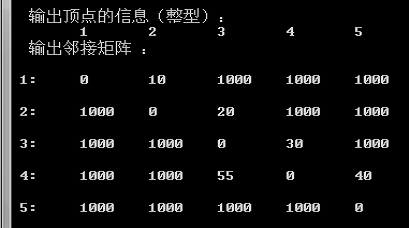
  3. F10单步调试到结束可以在DOS窗口中看到矩阵中相应的位置已经改变

Shift+F5退出调试,完成调试演示.


只有注册用户登录后才能发表评论。
网站导航: