转自:http://jaskell.blogbus.com/logs/3249971.html
一、同余
我们来了解一下什么是“同余”。简单来说就是,如果两个数都除以某个数能够有相同的余数,那么我们就说这两个数“同余”。不过这次我们用严谨的数学概念来表述:
两个整数 a,b,若它们除以整数 m 所得的余数相等,则称 a,b 对于模 m 同余
记作 
读作 a 同余于 b 模 m ,或读作 a 与 b 关于模 m 同余。
比如 
我们再来了解一下相关的性质:
- 如果
 ,那么 m | (a − b) ,这里 m | (a − b) 表示 (a − b) 能被 m 整除
,那么 m | (a − b) ,这里 m | (a − b) 表示 (a − b) 能被 m 整除
- 如果
 ,
,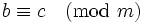 , 那么
, 那么
- 如果
 ,
, , 那么
, 那么 ,
, ,
,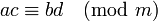 ,
,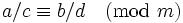
- 如果
 , 那么
, 那么 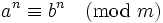
有了这些性质,判断两个数是否同余就可以用更简单的方法了。根据性质一,原来我们需要判断 (a mod m) == (b mod m)
是否为真,现在就可以直接判断 (a - b) mod m == 0
是否为真了。这样就把其中一次求余运算变为减法运算了。一般来说减法要比除法更容易在计算机上实现,运算速度也更快。
二、求余 (a * b * c * d) mod m = ?
由于计算机表示一个整数通常用 32bit 。而大量连乘运算则可能会导致整数溢出,这时我们就要利用求余一些性质来进行处理了。把以上式子转换为:
已知: (a * b) mod m == ((a mod m) * b) mod m
所以: (a * b * c * d) mod m = ((((((a mod m) * b) mod m) * c) mod m) * d) mod m
这样就把连乘运算分解了,每次可以先进行求余运算然后再进行乘法运算。