人在江湖

一，基础概念：

Probability of default(PD)：PD是巴塞尔协议中一个重要的参数，它用来计算某个客户或某批具有相似特征的客户贷款不还的概率。

Hosmer–Lemeshow test：PD中众多统计检验的其中一种，评估预测值与实际值在各个分组（subgroup, pool, bin）中拟合程度。

自由度：自由度是指随机变量中所含独立随机变量的个数n．如果这些独立随机变量受到k个约束条件的限制，那么自由度就变为n-k．

概率密度函数：是一个描述这个随机变量的输出值在某一个确定的取值点附近的可能性的函数。

卡方（χ²）分布：

设X₁, X₂,…,X_n是相互独立的随机变量且均服从标准正态分布N(0，1)，则随机变量

                    χ²= X₁²+X₂²+…+X_n

的分布称为服从自由度为n的χ²分布，记为χ²～χ²(n)

卡方分布的密度函数图为：

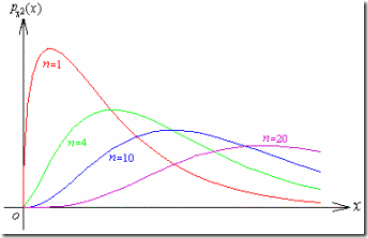
二， Hosmer–Lemeshow test的使用方法

Hosmer–Lemeshow test 的统计量是:

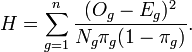
这里 O_g, E_g, N_g, and π_g 示观察到的事件，预期的事件，观察数, 预测的第g^th组的风险（在PD模型中，）， n是组数. 这个统计量符合自由度为n-2或n的卡方分布。

其他统计量都很直白，解释一下E_g的计算：实际应用中，可以用当前分组的违约概率 x 当前分组的观测值数目。

有了统计量的值之后，下一步计算就要依靠“这个统计量符合自由度为n-2或n的卡方分布”了。那么什么时候用自由度为n，什么时候用自由度为n-2呢。在书Basel2 risk parameters里有这样一段解释在321页。这本书可以在我的skydrive里找到https://skydrive.live.com/?cid=D8B11F9BF86FECFA&id=D8B11F9BF86FECFA%211346&sc=documents#：

“When using the HSLS statistic as a measure of fit in the process of model finding, then
we say “in-sample”, because the model estimation sample and the sample on which the
measure of fit is computed are identically. In this case the distribution is F2 with G 2
degrees  of  freedom.  When  using  the  HSLS  statistic  for  backtesting,  we  say  “out-of-
sample”,  because  there  is  no  observation  coexistent  in  the  estimation  sample  and  the
validation sample. ”

如果理解没错的话，在建模验证阶段，自由度是n-2, 模型建好之后，自由度都是n。

卡方检验P值的计算方式是1 - 特定自由度下卡方的的CDF，详见wikipedia：http://en.wikipedia.org/wiki/Chi-square_distribution中Table of χ² value vs P value部分

CDF指的是Cumulative distribution function，就是分布函数，详见wikipedia: http://en.wikipedia.org/wiki/Cumulative_distribution_function