#
这到底是怎样一个问题呢?还是用例子说明吧:
public class Parameter{
static void aMethod(){
int a=1; //定义一个int a
change(a);
System.out.println(a);
}
static void change(int a){ //将传入的a加1
a++;
}
public static void main(String[] args){
aMethod(); //执行并输出
}
}
猜猜程序的输出会是什么呢?1还是2?结果是1。为什么呢?
因为a是int 数据,所以作为参数传递的时候,a并没真正传入change(a).传入的是a的一个副本。所以change不管怎么对a进行处理都不会改变aMethod中a的值。
那么有没有办法通过外部的一个方法改变另一个方法里的值呢?当然有,只要使用对象的引用也叫句柄。说起来文绉绉的倒不如举个例子:
import java.util.*; //LinkedList要用到这个包
public class Parameter{
static void aMethod(){
LinkedList a = new LinkedList(); //生成一个LinkedList a对象
a.add("a");
change(a);
for(int i=0;i<a.size();i++){ //将链表中所有数据输出
System.out.println(a.get(i).toString());
}
}
static void change(LinkedList a){ //将传入的a加1
a.add("b"); //为a中再添加一个b
}
public static void main(String[] args){
aMethod(); //执行并输出
}
}
输出的结果是:
a
b
这说明了什么?说明change(LinkedList a)方法已经改变了a中的值。那么为什么a是对象就可以改变呢?我们将a传入change方法的时候传入的不是某个对象,而是这个对象的引用(或者叫做句柄)插入一句,什么是句柄?比如你,作为一个人,是一个对象,引用(句柄)就是你的身份证号码。当我们把引用作为参数传入方法的时候,引用同样也进行了复制,但复制后的引用指向同一个对象,所以change()里对a 的改变其实也就是对aMethod()里a的改变,因为他们是同一个对象!
是不是说只要是对象就可以了呢?不一定!
比如String类型的数据,即使你这样生成一个String a对象
String a = new String("go to hell");
a的确是一个对象,但是在a的引用复制的时候,原来的对象也会丢失。其实String 类型的数据在每次改变应用的时候都会清楚原来的对象。
比如在你这么使用的时候:
String a="you";//第一行
a=a+"are fool";//第二行
第一行的a和第二行的a所代表的是完全不同的对象。所以说如果程序里要对String进行大量改变的时候建议不要使用String,如果不小心使用了,你的程序将莫名其妙地占用大量的内存。不用String用什么?用StringBuffer!
不想说得太过于文绉绉,其实序列化,说白了就是将对象以文件的形式保存起来,反序列化,顾名思义,就是将对象文件转化为程序中的对象。一个对象如果要被序列化则必须实现Serializable接口(implements Serializable)。
序列化:
在这一过程中需要用到java.io包中的地两个类:FileOutputSteam 和ObjectOutputSteam
下面是一个将LinkedList对象序列化的简单例子,LinkedList已经实现了Serializable接口(implements Serializable),方法(Method)如下:
import java.io.*;
...//外部代码
public static void OutputObject() throws
FileNotFoundException,IOException{
LinkedList ll=new LinkedList();
FileOutputStream fos=new FileOutputStream("object");
ObjectOutputStream oos=new ObjectOutputStream(fos);
oos.writeObject(ll);
}
...//外部代码
关键代码就是三行,相当容易。
反序列化:
这一过程要用到FileInputStream和ObjectInputSteam,都在java.io包里
...//外部代码
public static Object InputObject() throws FileNotFoundException,
IOException, ClassNotFoundException{
FileInputStream fis=new FileInputStream("object");
ObjectInputStream ois=new ObjectInputStream(fis);
return ois.readObject();//返回对象
}
...//外部代码
关键代码就是两行。
当然这只是一个简单的入门,如果你被老外的书整晕了的话,上面这两段代码是很好的参考。
在java中,我们可以通过两种方式来获取随机数(generating a random number)一种是大家熟悉的java.lang.Math.Random()静态方法,另一种是创建java.util.Random对象。下面是两种方法的使用过程:
一.java.lang.Math.random()
在使用这一静态方法的时候,我们不需要import任何包,因为java.lang.*包是默认载入的,下面举例说面使用方法:
public class RandomTest{
public static void main(String[] args){
int i=Math.random();//random()会自动产生一个0.0-1.0的双精度随机数
System.out.println(i);//输出
i=Math.random()*1000;//产生0-1000的双精度随机数
System.out.println(i);
int b=(int)(Math.random()*1000);//产生0-1000的整数随机数
System.out.println(b);
}
}
二.创建java.util.Random对象
import java.util.random
public class RandomTest{
public static void main(String[] args){
Random random=new Random();//创建random对象
int intNumber=random.nextInt();//获取一个整型数
float floatNumber=random.nextFloat();//获取一个浮点数(0-1)
double doubleNumber=random.nextDouble();//获取双精度数(0-1)
boolean booleanNumber=random.nextBoolean();//获取boolean数
System.out.println("intNumber:"+intNumber);
System.out.println("floatNumber:"+floatNumber);
System.out.println("doubleNumber:"+doubleNumber);
System.out.println("booleanNumber:"+booleanNumber);
}
}
random在产生随机数的时候使用当前的时间作为基数,我们可以同过System.currentTimeMillis()来获取这个基数。当然我们也可以指定基数:
Random random=new Random(100);
同一基数所产生的随机数序列是一样的,可以用下面这一段程序进行印证:
import java.util.random
public class RandomTest{
public static void main(String[] args){
Random random1=new Random(100);
Random random2=new Random(100);
for(int i=0;i<5;i++){
System.out.print(random1.nextInt()+"\t");
System.out.println(random2.nextInt()+"\t");
System.out.println("---------------------------------");
}
}
}
我们可以发现random1和random2所产生的随机数是相同的。
根据约定,在使用java编程的时候应尽可能的使用现有的类库,当然你也可以自己编写一个排序的方法,或者框架,但是有几个人能写得比JDK里的还要好呢?使用现有的类的另一个好处是代码易于阅读和维护,这篇文章主要讲的是如何使用现有的类库对数组和各种Collection容器进行排序,(文章中的一部分例子来自《Java Developers Almanac 1.4》)
首先要知道两个类:java.util.Arrays和java.util.Collections(注意和Collection的区别)Collection是集合框架的顶层接口,而Collections是包含了许多静态方法。我们使用Arrays对数组进行排序,使用 Collections对结合框架容器进行排序,如ArraysList,LinkedList等。
例子中都要加上import java.util.*和其他外壳代码,如类和静态main方法,我会在第一个例子里写出全部代码,接下来会无一例外的省略。
对数组进行排序
比如有一个整型数组:
int[] intArray = new int[] {4, 1, 3, -23};
我们如何进行排序呢?你这个时候是否在想快速排序的算法?看看下面的实现方法:
import java.util.*;
public class Sort{
public static void main(String[] args){
int[] intArray = new int[] {4, 1, 3, -23};
Arrays.sort(intArray);
}
}
这样我们就用Arrays的静态方法sort()对intArray进行了升序排序,现在数组已经变成了{-23,1,3,4}.
如果是字符数组:
String[] strArray = new String[] {"z", "a", "C"};
我们用:
Arrays.sort(strArray);
进行排序后的结果是{C,a,z},sort()会根据元素的自然顺序进行升序排序。如果希望对大小写不敏感的话可以这样写:
Arrays.sort(strArray, String.CASE_INSENSITIVE_ORDER);
当然我们也可以指定数组的某一段进行排序比如我们要对数组下表0-2的部分(假设数组长度大于3)进行排序,其他部分保持不变,我们可以使用:
Arrays.sort(strArray,0,2);
这样,我们只对前三个元素进行了排序,而不会影响到后面的部分。
当然有人会想,我怎样进行降序排序?在众多的sort方法中有一个
我们使用Comparator获取一个反序的比较器即可,Comparator会在稍后讲解,以前面的intArray[]为例:
Arrays.sort(intArray,Comparator.reverseOrder());
这样,我们得到的结果就是{4,3,1,-23}。如果不想修改原有代码我们也可以使用:
Collections.reverse(Arrays.asList(intArray));
得到该数组的反序。结果同样为4,3,1,-23}。
现在的情况变了,我们的数组里不再是基本数据类型(primtive type)或者String类型的数组,而是对象数组。这个数组的自然顺序是未知的,因此我们需要为该类实现Comparable接口,比如我们有一个Name类:
class Name implements Comparable<Name>{
public String firstName,lastName;
public Name(String firstName,String lastName){
this.firstName=firstName;
this.lastName=lastName;
}
public int compareTo(Name o) { //实现接口
int lastCmp=lastName.compareTo(o.lastName);
return (lastCmp!=0?lastCmp:firstName.compareTo(o.firstName));
}
public String toString(){ //便于输出测试
return firstName+" "+lastName;
}
}
这样,当我们对这个对象数组进行排序时,就会先比较lastName,然后比较firstName 然后得出两个对象的先后顺序,就像compareTo(Name o)里实现的那样。不妨用程序试一试:
import java.util.*;
public class NameSort {
public static void main(String[] args) {
Name nameArray[] = {
new Name("John", "Lennon"),
new Name("Karl", "Marx"),
new Name("Groucho", "Marx"),
new Name("Oscar", "Grouch")
};
Arrays.sort(nameArray);
for(int i=0;i<nameArray.length;i++){
System.out.println(nameArray[i].toString());
}
}
}
结果正如我们所愿:
Oscar Grouch
John Lennon
Groucho Marx
Karl Marx
对集合框架进行排序
如果已经理解了Arrays.sort()对数组进行排序的话,集合框架的使用也是大同小异。只是将Arrays替换成了Collections,注意Collections是一个类而Collection是一个接口,虽然只差一个"s"但是它们的含义却完全不同。
假如有这样一个链表:
LinkedList list=new LinkedList();
list.add(4);
list.add(34);
list.add(22);
list.add(2);
我们只需要使用:
Collections.sort(list);
就可以将ll里的元素按从小到大的顺序进行排序,结果就成了:
[2, 4, 22, 34]
如果LinkedList里面的元素是String,同样会想基本数据类型一样从小到大排序。
如果要实现反序排序也就是从达到小排序:
Collections.sort(list,Collectons.reverseOrder());
如果LinkedList里面的元素是自定义的对象,可以像上面的Name对象一样实现Comparable接口,就可以让Collection.sort()为您排序了。
如果你想按照自己的想法对一个对象进行排序,你可以使用
这个方法进行排序,在给出例子之前,先要说明一下Comparator的使用,
Comparable接口的格式:
public interface Comparator<T> {
int compare(T o1, T o2);
}
其实Comparator里的int compare(T o1,T o2)的写法和Comparable里的compareTo()方法的写法差不多。在上面的Name类中我们的比较是从LastName开始的,这是西方人的习惯,到了中国,我们想从fristName开始比较,又不想修改原来的代码,这个时候,Comparator就可以派上用场了:
final Comparator<Name> FIRST_NAME_ORDER=new Comparator<Name>() {
public int compare(Name n1, Name n2) {
int firstCmp=n1.firstName.compareTo(n2.firstName);
return (firstCmp!=0?firstCmp:n1.lastName.compareTo
(n2.firstName));
}
};
这样一个我们自定义的Comparator FIRST_NAME_ORDER就写好了。
将上个例子里那个名字数组转化为List:
List<Name> list=Arrays.asList(nameArray);
Collections.sort(list,FIRST_NAME_ORDER);
这样我们就成功的使用自己定义的比较器设定排序。
在openssl或其他密码相关的资料中,我们经常看到对称加密算法有ECB、CBC之类加密模式的简称,到底这些加密模式是什么呢?它们之间有什么不同呢,今天就是为大家解开这个迷。
在现有的对称加密算法中,主要有4种加密处理模式,这4种加密处理模式一般是针对块加密算法而言的,如DES算法。这4种加密模式罗列如下:
模式中文描述 英文名称(Openssl缩写)
电子密码本模式 Electronic Code Book(ECB)
加密块链模式 Cipher Block Chaining(CBC)
加密反馈模式 Cipher Feedback Mode(CFB)
输出反馈模式 Output Feedback Mode(OFB)
下面我们分别介绍这4种加密模式。
**********************************************************************
【电子密码本模式】
这种模式是最早采用和最简单的模式,它将加密的数据分成若干组,每组的大小跟加密密钥长度相同,然后每组都用相同的密钥进行加密。比如DES算法,一个64位的密钥,如果采用该模式加密,就是将要加密的数据分成每组64位的数据,如果最后一组不够64位,那么就补齐为64位,然后每组数据都采用DES算法的64位密钥进行加密。下图:
_______________________
My name |is Drago|nKing
-----------------------
上图“My name is DragonKing”这句话每8个字符(64位)作为一块,然后使用一个相同的64位的密钥对每个块进行加密,最后一块不足64位,就补齐后再进行加密。
可以看到,因为ECB方式每64位使用的密钥都是相同的,所以非常容易获得密文进行密码破解,此外,因为每64位是相互独立的,有时候甚至不用破解密码,只要简单的将其中一块替换就可以达到黑客目的。
【加密块链模式】
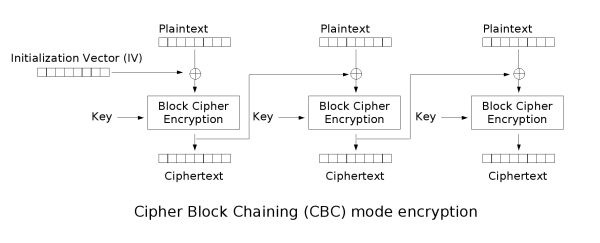
从这两个图中大家可以看到,CBC模式的加密首先也是将明文分成固定长度(64位)的块(P0,P1...),然后将前面一个加密块输出的密文与下一个要加密的明文块进行XOR(异或)操作计算,将计算结果再用密钥进行加密得到密文。第一明文块加密的时候,因为前面没有加密的密文,所以需要一个初始化向量(IV)。跟ECB方式不一样,通过连接关系,使得密文跟明文不再是一一对应的关系,破解起来更困难,而且克服了只要简单调换密文块可能达到目的的攻击。
但是该加密模式的缺点是不能实时解密,也就是说,必须等到每8个字节都接受到之后才能开始加密,否则就不能得到正确的结果。这在要求实时性比较高的时候就显得不合适了。所以才有了下面两种加密模式。
【加密反馈模式】
加密反馈模式为了克服必须等待8个字节全部得到才能进行解密的缺点,采用了一个64位(8个字节)的位移寄存器来获得密文,如下图所示:
上面两个图中C2、C3以及P10等都是一个字节(8位)的数据,所以能够实现字符的实时加密和解密,不用再等到8个字节都接受到之后再进行解密。图示是在进行第10个字节数据的加密和解密过程,在该过程中,先从移位寄存器取8个字节的数据(C2到C9)用密钥进行加密,然后取加密数据最左边的一个字节跟输入的明文P10进行XOR(异或)操作,得到的值作为输出密文C10,同时将C10送入到移位寄存器中。
需要注意的是,如果其中有一个字节的密文在传输的时候发生错误(即使是其中的一位),那么它出现在移位寄存器期间解密的8个字节的数据都会得不到正确的解密结果,当然,这8个字节过去之后,依然可以得到正确的解密结果。但是一个比特错误就影响到8个字节(64个比特)的正确结果,导致鲁棒性太差,所以就又提出了下面的加密模式OFB。
【输出反馈模式】
输出反馈模式OFB跟CFB几乎是一样的,除了其以为寄存器的输入数据稍微有一点不同之外,如下图:
可以看到,这种方法因为没有采用密文作为加密的数据,所以克服了由于传输过程中由于单个比特导致64个相关比特解密失败的情况,在本模式下,如果一个比特发生错误了,那么只会影响其本身对应的一个比特,而不会影响别的。但是相对于其它模式,因为数据之间相关性小,这种加密模式是比较不安全的,所以在应用的时候除非特别需要,一般不提倡应用OFB模式。
原文地址 http://hi.baidu.com/msingle/blog/item/e9d7cd455e02ed25cffca3a6.html
其他的一些补充:
■ 缩写说明 ■
IN - 输入向量
OUT - 输出向量(未用于和明文加密前)
ENC - 加密算法
K - 加密密钥
P - 明文
C - 密文
XOR - 异或
<< - 左移
BSIZE - 算法的加密块尺寸
COUNT - 计数器
------------------------------------------------------------------------------
计数器(CTR)模式: IN(N) = ENC(K, COUNT++), C(N) = IN(N) XOR P(N);CTR 模式被广泛用于 ATM 网络安全和 IPSec应用中,相对于其它模式而言,CRT模式具有如下特点:
■ 硬件效率:允许同时处理多块明文 / 密文。
■ 软件效率:允许并行计算,可以很好地利用 CPU 流水等并行技术。
■ 预处理: 算法和加密盒的输出不依靠明文和密文的输入,因此如果有足够的保证安全的存储器,加密算法将仅仅是一系列异或运算,这将极大地提高吞吐量。
■ 随机访问:第 i 块密文的解密不依赖于第 i-1 块密文,提供很高的随机访问能力
■ 可证明的安全性:能够证明 CTR 至少和其他模式一样安全(CBC, CFB, OFB, ...)
■ 简单性:与其它模式不同,CTR模式仅要求实现加密算法,但不要求实现解密算法。对于 AES 等加/解密本质上不同的算法来说,这种简化是巨大的。
■ 无填充,可以高效地作为流式加密使用。
------------------------------------------------------------------------------
密文块链接(CBC)模式:IN(N) = P(N) XOR C(N-1), C(N) = ENC(K, IN(N));在 CTR出现前广泛使用的块加密模式,用于安全的分组(迭代式)加密和认证。
------------------------------------------------------------------------------
密文反馈 (CFB) 模式: IN(N) = C(N-1) << (BSIZE-j), C(N) = ENC(K, IN(N)) << (BSIZE-j) XOR P(N). 其中 j 为每次加密的位数。CFB 模式与 CBC 模式原理相似,但一次仅处理 j 位数据,其余 BLOCKSIZE - j 位丢弃。由于以上性质,CFB 模式可以在不损失安全性的前提下,将块加密变为流式加密。但是该模式也是比较浪费的,因为在每轮加解密中都丢弃了大部分结果(j 通常为一字节(8 位),块加密算法中每块的尺寸通常为64、128 或 256 位不等)。
------------------------------------------------------------------------------
输出反馈 (OFB) 模式:IN(N) = OUT(N-1) << (BSIZE-j), C(N) = ENC(K, IN(N)) << (BSIZE-j) XOR P(N), OUT(N) = ENC(K, IN(N)) << (BSIZE-j). 该模式与 CFB 模式基本相同,只不过本次输入是上次迭代中尚未与明文异或时的输出。 与 CFB 模式一样, OFB 模式也可以作为流加密模式使用,除此之外,由于每次迭代的输入不是上次迭代的密文,从而保证了较强的容错能力, 即: 对一块(一字节)密文的传输错误不会影响到后继密文。但是,由于输入没有经过密文叠加使得其抗篡改攻击的能力较差,通常需要与消息验
证算法或数字签名算法配套使用。OFB 通常用于噪音水平较高的通信连接以及一般的流式应用中。
------------------------------------------------------------------------------
电码本(ECB)模式: IN(N) = P(N), C(N) = ENC(K, IN(N)). 最简单但最不安全的加密方式。每次迭代的输入都使用相同密钥进行无变换的直接加密。对于同样的明文片断,总会产生相同的,与之对应的密文段。抗重复统计和结构化分析的能力较差。一次性加密的最坏情况 (即:每次输入的明文都小于等于 BSIZE 时) 就是电码本模式。 仅在一次一密,或传出极少数据时考虑使用 ECB 模式。
转自:IaWeN's Blog-iawen,原创,安全,破解视频,网页设计,影视后期,AE特效
链接:http://www.iawen.com/read.php?296
形参出现在函数定义中,在整个函数体内都可以使用, 离开该函数则不能使用。
实参出现在主调函数中,进入被调函数后,实参变量也不能使用。
形参和实参的功能是作数据传送。发生函数调用时, 主调函数把实参的值传送给被调函数的形参从而实现主调函数向被调函数的数据传送。
1.形参变量只有在被调用时才分配内存单元,在调用结束时, 即刻释放所分配的内存单元。因此,形参只有在函数内部有效。 函数调用结束返回主调函数后则不能再使用该形参变量。
2.实参可以是常量、变量、表达式、函数等, 无论实参是何种类型的量,在进行函数调用时,它们都必须具有确定的值, 以便把这些值传送给形参。 因此应预先用赋值,输入等办法使实参获得确定值。
3.实参和形参在数量上,类型上,顺序上应严格一致, 否则会发生“类型不匹配”的错误。
4.函数调用中发生的数据传送是单向的。 即只能把实参的值传送给形参,而不能把形参的值反向地传送给实参。 因此在函数调用过程中,形参的值发生改变,而实参中的值不会变化。
5.当形参和实参不是指针类型时,在该函数运行时,形参和实参是不同的变量,他们在内存中位于不同的位置,形参将实参的内容复制一份,在该函数运行结束的时候形参被释放,而实参内容不会改变。 而如果函数的参数是指针类型变量,在调用该函数的过程中,传给函数的是实参的地址,在函数体内部使用的也是实参的地址,即使用的就是实参本身。所以在函数体内部可以改变实参的值
什么是对称加密技术?
对称加密采用了对称密码编码技术,它的特点是文件加密和解密使用相同的密钥,即加密密钥也可以用作解密密钥,这种方法在密码学中叫做对称加密算法,对称加密算法使用起来简单快捷,密钥较短,且破译困难,除了数据加密标准(DES),另一个对称密钥加密系统是国际数据加密算法(IDEA),它比DES的加密性好,而且对计算机功能要求也没有那么高。IDEA加密标准由PGP(Pretty Good Privacy)系统使用。
对称加密算法在电子商务交易过程中存在几个问题:
1、要求提供一条安全的渠道使通讯双方在首次通讯时协商一个共同的密钥。直接的面对面协商可能是不现实而且难于实施的,所以双方可能需要借助于邮件和电话等其它相对不够安全的手段来进行协商;
2、密钥的数目难于管理。因为对于每一个合作者都需要使用不同的密钥,很难适应开放社会中大量的信息交流;
3、对称加密算法一般不能提供信息完整性的鉴别。它无法验证发送者和接受者的身份;
4、对称密钥的管理和分发工作是一件具有潜在危险的和烦琐的过程。对称加密是基于共同保守秘密来实现的,采用对称加密技术的贸易双方必须保证采用的是相同的密钥,保证彼此密钥的交换是安全可靠的,同时还要设定防止密钥泄密和更改密钥的程序。
假设两个用户需要使用对称加密方法加密然后交换数据,则用户最少需要2个密钥并交换使用,如果企业内用户有n个,则整个企业共需要n×(n-1) 个密钥,密钥的生成和分发将成为企业信息部门的恶梦。
常见的对称加密算法有DES、3DES、Blowfish、IDEA、RC4、RC5、RC6和AES
什么是非对称加密技术
1976年,美国学者Dime和Henman为解决信息公开传送和密钥管理问题,提出一种新的密钥交换协议,允许在不安全的媒体上的通讯双方交换信息,安全地达成一致的密钥,这就是“公开密钥系统”。相对于“对称加密算法”这种方法也叫做“非对称加密算法”。
与对称加密算法不同,非对称加密算法需要两个密钥:公开密钥(publickey)和私有密钥(privatekey)。公开密钥与私有密钥是一对,如果用公开密钥对数据进行加密,只有用对应的私有密钥才能解密;如果用私有密钥对数据进行加密,那么只有用对应的公开密钥才能解密。因为加密和解密使用的是两个不同的密钥,所以这种算法叫作非对称加密算法。
非对称加密算法实现机密信息交换的基本过程是:甲方生成一对密钥并将其中的一把作为公用密钥向其它方公开;得到该公用密钥的乙方使用该密钥对机密信息进行加密后再发送给甲方;甲方再用自己保存的另一把专用密钥对加密后的信息进行解密。甲方只能用其专用密钥解密由其公用密钥加密后的任何信息。
非对称加密算法的保密性比较好,它消除了最终用户交换密钥的需要,但加密和解密花费时间长、速度慢,它不适合于对文件加密而只适用于对少量数据进行加密。
如果企业中有n个用户,企业需要生成n对密钥,并分发n个公钥。由于公钥是可以公开的,用户只要保管好自己的私钥即可(企业分发后一般保存的是私钥,用户拿的是公钥),因此加密密钥的分发将变得十分简单。同时,由于每个用户的私钥是唯一的,其他用户除了可以可以通过信息发送者的公钥来验证信息的来源是否真实,还可以确保发送者无法否认曾发送过该信息。非对称加密的缺点是加解密速度要远远慢于对称加密,在某些极端情况下,甚至能比非对称加密慢上1000倍。
非对称加密的典型应用是数字签名。
常见的非对称加密算法有:RSA、ECC(移动设备用)、Diffie-Hellman、El Gamal、DSA(数字签名用)
企业加密系统应用 常用加密算法介绍
对称加密、非对称加密、hash加密(md5加密是典型应用)
Hash算法
Hash算法特别的地方在于它是一种单向算法,用户可以通过Hash算法对目标信息生成一段特定长度的唯一的Hash值,却不能通过这个Hash值重新获得目标信息。因此Hash算法常用在不可还原的密码存储、信息完整性校验等。
常见的Hash算法有MD2、MD4、MD5、HAVAL、SHA
加密算法的效能通常可以按照算法本身的复杂程度、密钥长度(密钥越长越安全)、加解密速度等来衡量。上述的算法中,除了DES密钥长度不够、MD2速度较慢已逐渐被淘汰外,其他算法仍在目前的加密系统产品中使用。
对于较长的明文进行加密需要进行分块加密,但是直接加密(ecb)不容易隐藏模式,用OpenCV写了个程序论证了一下
ECB
优点就是简单,可以并行计算,不会迭代误差
缺点就是隐藏不了模式

CBC
需要初始化向量IV,来加密第一块C0.
有点就是比ECB好
缺点不利于并行计算、误差会迭代,还需要初始向量

加密算法为简单的位翻转
- #define bitrev(b) (((b)<<7)&0x80) | \
- (((b)<<5)&0x40) | \
- (((b)<<3)&0x20) | \
- (((b)<<1)&0x10) | \
- (((b)>>1)&0x08) | \
- (((b)>>3)&0x04) | \
- (((b)>>5)&0x02) | \
- (((b)>>7)&0x01)
#define bitrev(b) (((b)<<7)&0x80) | \
(((b)<<5)&0x40) | \
(((b)<<3)&0x20) | \
(((b)<<1)&0x10) | \
(((b)>>1)&0x08) | \
(((b)>>3)&0x04) | \
(((b)>>5)&0x02) | \
(((b)>>7)&0x01)
ECB加密,就是直接分块进行加密
- for(int i=0;i<grey->width;i++)
- for(int j=0;j<grey->height;j++)
- grey->imageData[j*grey->width+i]=bitrev(grey->imageData[j*grey->width+i]);
- cvNamedWindow("ecb");
- cvShowImage("ecb", grey);
for(int i=0;i<grey->width;i++)
for(int j=0;j<grey->height;j++)
grey->imageData[j*grey->width+i]=bitrev(grey->imageData[j*grey->width+i]);
cvNamedWindow("ecb");
cvShowImage("ecb", grey);
CBC加密,与上一块密文异或后加密
- for(int i=0;i<grey->width;i++)
- for(int j=0;j<grey->height;j++)
- if(i!=0&&j!=0)
- grey->imageData[j*grey->width+i]=bitrev(grey->imageData[j*grey->width+i]^grey->imageData[j*grey->width+i-1]);
- else
- grey->imageData[0]=grey->imageData[0]^IV;
- cvNamedWindow("cbc");
- cvShowImage("cbc", grey);
一. AES对称加密:

AES加密

分组
二. 分组密码的填充

分组密码的填充
e.g.:

三. 流密码:

四. 分组密码加密中的四种模式:
3.1 ECB模式

优点:
1.简单;
2.有利于并行计算;
3.误差不会被传送;
缺点:
1.不能隐藏明文的模式;
2.可能对明文进行主动攻击;

3.2 CBC模式:

优点:
1.不容易主动攻击,安全性好于ECB,适合传输长度长的报文,是SSL、IPSec的标准。
缺点:
1.不利于并行计算;
2.误差传递;
3.需要初始化向量IV
3.3 CFB模式:

优点:
1.隐藏了明文模式;
2.分组密码转化为流模式;
3.可以及时加密传送小于分组的数据;
缺点:
1.不利于并行计算;
2.误差传送:一个明文单元损坏影响多个单元;
3.唯一的IV;
3.4 OFB模式:

优点:
1.隐藏了明文模式;
2.分组密码转化为流模式;
3.可以及时加密传送小于分组的数据;
缺点:
1.不利于并行计算;
2.对明文的主动攻击是可能的;
3.误差传送:一个明文单元损坏影响多个单元;
PKCS#5填充方式
参与运算的两个值,如果两个相应bit位相同,则结果为0,否则为1。
即:
0^0 = 0,
1^0 = 1,
0^1 = 1,
1^1 = 0
按位异或的3个特点:
(1) 0^0=0,0^1=1 0异或任何数=任何数
(2) 1^0=1,1^1=0 1异或任何数-任何数取反
(3) 任何数异或自己=把自己置0
按位异或的几个常见用途:
(1) 使某些特定的位翻转
例如对数10100001的第2位和第3位翻转,则可以将该数与00000110进行按位异或运算。
10100001^00000110 = 10100111
(2) 实现两个值的交换,而不必使用临时变量。
例如交换两个整数a=10100001,b=00000110的值,可通过下列语句实现:
a = a^b; //a=10100111
b = b^a; //b=10100001
a = a^b; //a=00000110
(3) 在汇编语言中经常用于将变量置零:
xor a,a
(4) 快速判断两个值是否相等
举例1: 判断两个整数a,b是否相等,则可通过下列语句实现:
return ((a ^ b) == 0)
举例2: Linux中最初的ipv6_addr_equal()函数的实现如下:
static inline int ipv6_addr_equal(const struct in6_addr *a1, const struct in6_addr *a2)
{
return (a1->s6_addr32[0] == a2->s6_addr32[0] &&
a1->s6_addr32[1] == a2->s6_addr32[1] &&
a1->s6_addr32[2] == a2->s6_addr32[2] &&
a1->s6_addr32[3] == a2->s6_addr32[3]);
}
可以利用按位异或实现快速比较, 最新的实现已经修改为:
static inline int ipv6_addr_equal(const struct in6_addr *a1, const struct in6_addr *a2)
{
return (((a1->s6_addr32[0] ^ a2->s6_addr32[0]) |
(a1->s6_addr32[1] ^ a2->s6_addr32[1]) |
(a1->s6_addr32[2] ^ a2->s6_addr32[2]) |
(a1->s6_addr32[3] ^ a2->s6_addr32[3])) == 0);
}
5 应用通式:
对两个表达式执行按位异或。
result = expression1 ^ expression2
参数
result
任何变量。
expression1
任何表达式。
expression2
任何表达式。
说明
^ 运算符查看两个表达式的二进制表示法的值,并执行按位异或。该操作的结果如下所示:
0101 (expression1)1100 (expression2)----1001 (结果)当且仅当只有一个表达式的某位上为 1 时,结果的该位才为 1。否则结果的该位为 0。
只能用于整数
下面这个程序用到了“按位异或”运算符:
class E
{ public static void main(String args[ ])
{
char a1='十' , a2='点' , a3='进' , a4='攻' ;
char secret='8' ;
a1=(char) (a1^secret);
a2=(char) (a2^secret);
a3=(char) (a3^secret);
a4=(char) (a4^secret);
System.out.println("密文:"+a1+a2+a3+a4);
a1=(char) (a1^secret);
a2=(char) (a2^secret);
a3=(char) (a3^secret);
a4=(char) (a4^secret);
System.out.println("原文:"+a1+a2+a3+a4);
}
}
就是加密啊解密啊
char类型,也就是字符类型实际上就是整形,就是数字.
计算机里面所有的信息都是整数,所有的整数都可以表示成二进制的,实际上计算机只认识二进制的.
位运算就是二进制整数运算啦.
两个数按位异或意思就是从个位开始,一位一位的比.
如果两个数相应的位上一样,结果就是0,不一样就是1
所以111^101=010
那加密的过程就是逐个字符跟那个secret字符异或运算.
解密的过程就是密文再跟同一个字符异或运算
010^101=111
至于为什么密文再次异或就变原文了,这个稍微想下就知道了..