2008年7月7日
这回是帮自己家小妞的网店做的店标,宣传什么的,所以风格相似恰恰是我想要的。

网店的Logo。那大腿不是别人的,正是韩国歌星宝儿……

她跟我说上面这张图最大的问题就在于太有夜店风格,与她的店不符。不过用着用着,她自己倒也喜欢上了。

这个是刚出炉的5月新款的预告,照片里的人可全是她……
在文本分类的过程中,特征(也可以简单的理解为“词”)从人类能够理解的形式转换为计算机能够理解的形式时,实际上经过了两步骤的量化——特征选择阶段的重要程度量化和将具体文本转化为向量时的特征权重量化。初次接触文本分类的人很容易混淆这两个步骤使用的方法和各自的目的,因而我经常听到读者有类似“如何使用TFIDF做特征选择”或者“卡方检验量化权重后每篇文章都一样”等等困惑。
文本分类本质上也是一个模式识别的问题,因此我想借用一个更直观的例子来说说特征选择和权重量化到底各自是什么东西,当然,一旦解释清楚,你马上就会觉得文本分类这东西实在白痴,实在没什么技术含量,你也就不会再继续看我的技术博客,不过我不担心,因为你已经踏上了更光明的道路(笑),我高兴还来不及。
想想通过指纹来识别一个人的身份,只看一个人的指纹,当然说不出他姓甚名谁,识别的过程实际上是比对的过程,要与已有的指纹库比较,找出相同的,或者说相似到一定程度的那一个。
首要的问题是,人的指纹太复杂,包含太多的位置和几何形状,要完全重现一个人的指纹,存储和计算都是大麻烦。因此第一步总是一个特征选择的问题,我们把全人类的指纹都统计一下,看看哪几个位置能够最好的区分不同的人。显然不同的位置效果很不一样,在有的位置上,我的指纹是是什么形状,其他人也大都是这个形状,这个位置就不具有区分度,或者说不具有表征性,或者说,对分类问题来说,它的重要程度低。这样的位置我们就倾向于在识别的时候根本不看它,不考虑它。
那怎么看谁重要谁不重要呢?这就依赖于具体的选择方法如何来量化重要程度,对卡方检验和信息增益这类方法来说,量化以后的得分越大的特征就越重要(也就是说,有可能有些方法,是得分越小的越重要)。
比如说你看10个位置,他们的重要程度分别是:
1 2 3 4 5 6 7 8 9 10
(20,5,10,20,30,15,4,3,7, 3)
显然第1,第3,4,5,6个位置比其他位置更重要,而相对的,第1个位置又比第3个位置更重要。
识别时,我们只在那些重要的位置上采样。当今的指纹识别系统,大都只用到人指纹的5个位置(惊讶么?只要5个位置的信息就可以区分60亿人),这5个位置就是经过特征选择过程而得以保留的系统特征集合。假设这个就是刚才的例子,那么该集合应该是:
(第1个位置,第3个位置,第4个位置,第5个位置,第6个位置)
当然,具体的第3个位置是指纹中的哪个位置你自己总得清楚。
确定了这5个位置之后,就可以把一个人的指纹映射到这个只有5个维度的空间中,我们就把他在5个位置上的几何形状分别转换成一个具体的值,这就是特征权重的计算。依据什么来转换,就是你选择的特征权重量化方法,在文本分类中,最常用的就是TFIDF。
我想一定是“权重“这个词误导了所有人,让大家以为TFIDF计算出的值代表的是特征的重要程度,其实完全不是。例如我们有一位男同学,他的指纹向量是:
(10,3,4,20,5)
你注意到他第1个位置的得分(10)比第3个位置的得分(3)高,那么能说第1个位置比第3个位置重要么?如果再有一位女同学,她的指纹向量是:
(10,20,4,20,5)
看看,第1个位置得分(10)又比第3个位置(20)低了,那这两个位置到底哪个更重要呢?答案是第1个位置更重要,但这不是在特征权重计算这一步体现出来的,而是在我们特征选择的时候就确定了,第1个位置比第3个位置更重要。
因此要记住,通过TFIDF计算一个特征的权重时,该权重体现出的根本不是特征的重要程度!
那它代表什么?再看看两位同学的指纹,放到一起:
(10, 3,4,20,5)
(10,20,4,20,5)
在第三个位置上女同学的权重高于男同学,这不代表该女同学在指纹的这个位置上更“优秀“(毕竟,指纹还有什么优秀不优秀的分别么,笑),也不代表她的这个位置比男同学的这个位置更重要,3和20这两个得分,仅仅代表他们的”不同“。
在文本分类中也是如此,比如我们的系统特征集合只有两个词:
(经济,发展)
这两个词是使用卡方检验(特征选择)选出来的,有一篇文章的向量形式是
(2,5)
另一篇
(3,4)
这两个向量形式就是用TFIDF算出来的,很容易看出两篇文章不是同一篇,为什么?因为他们的特征权重根本不一样,所以说权重代表的是差别,而不是优劣。想想你说“经济这个词在第二篇文章中得分高,因此它在第二篇文章中比在第一篇文章中更重要“,这句话代表什么意义呢?你自己都不知道吧(笑)。
所以,当再说起使用TFIDF来计算特征权重时,最好把“权重“这个字眼忘掉,我们就把它说成计算得分好了(甚至”得分“也不太好,因为人总会不自觉的认为,得分高的就更重要),或者就仅仅说成是量化。
如此,你就再也不会拿TFIDF去做特征选择了。
小Tips:为什么有的论文里确实使用了TFIDF作特征选择呢?
严格说来并不是不可以,而且严格说来只要有一种方法能够从一堆特征中挑出少数的一些,它就可以叫做一种特征选择方法,就连“随机选取一部分“都算是一种,而且效果并没有差到惊人的地步哦!还是可以分对一大半的哦!所以有的人就用TFIDF的得分来把特征排排序,取得分最大的几个进入系统特征集合,效果也还行(毕竟,连随机选取效果也都还行),怎么说呢,他们愿意这么干就这么干吧。就像咱国家非得实行户口制度,这个制度说不出任何道理,也不见他带来任何好处,但不也没影响二十一世纪成为中国的世纪么,呵呵。
又小忙了几天。打算写一篇澄清特征选择和特征权重计算中许多容易误解的问题的文章,不知大家有没有兴趣。
从 SVM的那几张图可以看出来,SVM是一种典型的两类分类器,即它只回答属于正类还是负类的问题。而现实中要解决的问题,往往是多类的问题(少部分例外,例如垃圾邮件过滤,就只需要确定“是”还是“不是”垃圾邮件),比如文本分类,比如数字识别。如何由两类分类器得到多类分类器,就是一个值得研究的问题。
还以文本分类为例,现成的方法有很多,其中一种一劳永逸的方法,就是真的一次性考虑所有样本,并求解一个多目标函数的优化问题,一次性得到多个分类面,就像下图这样:
多个超平面把空间划分为多个区域,每个区域对应一个类别,给一篇文章,看它落在哪个区域就知道了它的分类。
看起来很美对不对?只可惜这种算法还基本停留在纸面上,因为一次性求解的方法计算量实在太大,大到无法实用的地步。
稍稍退一步,我们就会想到所谓“一类对其余”的方法,就是每次仍然解一个两类分类的问题。比如我们有5个类别,第一次就把类别1的样本定为正样本,其余2,3,4,5的样本合起来定为负样本,这样得到一个两类分类器,它能够指出一篇文章是还是不是第1类的;第二次我们把类别2 的样本定为正样本,把1,3,4,5的样本合起来定为负样本,得到一个分类器,如此下去,我们可以得到5个这样的两类分类器(总是和类别的数目一致)。到了有文章需要分类的时候,我们就拿着这篇文章挨个分类器的问:是属于你的么?是属于你的么?哪个分类器点头说是了,文章的类别就确定了。这种方法的好处是每个优化问题的规模比较小,而且分类的时候速度很快(只需要调用5个分类器就知道了结果)。但有时也会出现两种很尴尬的情况,例如拿一篇文章问了一圈,每一个分类器都说它是属于它那一类的,或者每一个分类器都说它不是它那一类的,前者叫分类重叠现象,后者叫不可分类现象。分类重叠倒还好办,随便选一个结果都不至于太离谱,或者看看这篇文章到各个超平面的距离,哪个远就判给哪个。不可分类现象就着实难办了,只能把它分给第6个类别了……更要命的是,本来各个类别的样本数目是差不多的,但“其余”的那一类样本数总是要数倍于正类(因为它是除正类以外其他类别的样本之和嘛),这就人为的造成了上一节所说的“数据集偏斜”问题。
因此我们还得再退一步,还是解两类分类问题,还是每次选一个类的样本作正类样本,而负类样本则变成只选一个类(称为“一对一单挑”的方法,哦,不对,没有单挑,就是“一对一”的方法,呵呵),这就避免了偏斜。因此过程就是算出这样一些分类器,第一个只回答“是第1类还是第2类”,第二个只回答“是第1类还是第3类”,第三个只回答“是第1类还是第4类”,如此下去,你也可以马上得出,这样的分类器应该有5 X 4/2=10个(通式是,如果有k个类别,则总的两类分类器数目为k(k-1)/2)。虽然分类器的数目多了,但是在训练阶段(也就是算出这些分类器的分类平面时)所用的总时间却比“一类对其余”方法少很多,在真正用来分类的时候,把一篇文章扔给所有分类器,第一个分类器会投票说它是“1”或者“2”,第二个会说它是“1”或者“3”,让每一个都投上自己的一票,最后统计票数,如果类别“1”得票最多,就判这篇文章属于第1类。这种方法显然也会有分类重叠的现象,但不会有不可分类现象,因为总不可能所有类别的票数都是0。看起来够好么?其实不然,想想分类一篇文章,我们调用了多少个分类器?10个,这还是类别数为5的时候,类别数如果是1000,要调用的分类器数目会上升至约500,000个(类别数的平方量级)。这如何是好?
看来我们必须再退一步,在分类的时候下功夫,我们还是像一对一方法那样来训练,只是在对一篇文章进行分类之前,我们先按照下面图的样子来组织分类器(如你所见,这是一个有向无环图,因此这种方法也叫做DAG SVM)
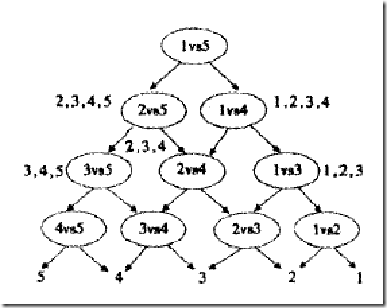
这样在分类时,我们就可以先问分类器“1对5”(意思是它能够回答“是第1类还是第5类”),如果它回答5,我们就往左走,再问“2对5”这个分类器,如果它还说是“5”,我们就继续往左走,这样一直问下去,就可以得到分类结果。好处在哪?我们其实只调用了4个分类器(如果类别数是k,则只调用k-1个),分类速度飞快,且没有分类重叠和不可分类现象!缺点在哪?假如最一开始的分类器回答错误(明明是类别1的文章,它说成了5),那么后面的分类器是无论如何也无法纠正它的错误的(因为后面的分类器压根没有出现“1”这个类别标签),其实对下面每一层的分类器都存在这种错误向下累积的现象。。
不过不要被DAG方法的错误累积吓倒,错误累积在一对其余和一对一方法中也都存在,DAG方法好于它们的地方就在于,累积的上限,不管是大是小,总是有定论的,有理论证明。而一对其余和一对一方法中,尽管每一个两类分类器的泛化误差限是知道的,但是合起来做多类分类的时候,误差上界是多少,没人知道,这意味着准确率低到0也是有可能的,这多让人郁闷。
而且现在DAG方法根节点的选取(也就是如何选第一个参与分类的分类器),也有一些方法可以改善整体效果,我们总希望根节点少犯错误为好,因此参与第一次分类的两个类别,最好是差别特别特别大,大到以至于不太可能把他们分错;或者我们就总取在两类分类中正确率最高的那个分类器作根节点,或者我们让两类分类器在分类的时候,不光输出类别的标签,还输出一个类似“置信度”的东东,当它对自己的结果不太自信的时候,我们就不光按照它的输出走,把它旁边的那条路也走一走,等等。
大Tips:SVM的计算复杂度
使用SVM进行分类的时候,实际上是训练和分类两个完全不同的过程,因而讨论复杂度就不能一概而论,我们这里所说的主要是训练阶段的复杂度,即解那个二次规划问题的复杂度。对这个问题的解,基本上要划分为两大块,解析解和数值解。
解析解就是理论上的解,它的形式是表达式,因此它是精确的,一个问题只要有解(无解的问题还跟着掺和什么呀,哈哈),那它的解析解是一定存在的。当然存在是一回事,能够解出来,或者可以在可以承受的时间范围内解出来,就是另一回事了。对SVM来说,求得解析解的时间复杂度最坏可以达到O(Nsv3),其中Nsv是支持向量的个数,而虽然没有固定的比例,但支持向量的个数多少也和训练集的大小有关。
数值解就是可以使用的解,是一个一个的数,往往都是近似解。求数值解的过程非常像穷举法,从一个数开始,试一试它当解效果怎样,不满足一定条件(叫做停机条件,就是满足这个以后就认为解足够精确了,不需要继续算下去了)就试下一个,当然下一个数不是乱选的,也有一定章法可循。有的算法,每次只尝试一个数,有的就尝试多个,而且找下一个数字(或下一组数)的方法也各不相同,停机条件也各不相同,最终得到的解精度也各不相同,可见对求数值解的复杂度的讨论不能脱开具体的算法。
一个具体的算法,Bunch-Kaufman训练算法,典型的时间复杂度在O(Nsv3+LNsv2+dLNsv)和O(dL2)之间,其中Nsv是支持向量的个数,L是训练集样本的个数,d是每个样本的维数(原始的维数,没有经过向高维空间映射之前的维数)。复杂度会有变化,是因为它不光跟输入问题的规模有关(不光和样本的数量,维数有关),也和问题最终的解有关(即支持向量有关),如果支持向量比较少,过程会快很多,如果支持向量很多,接近于样本的数量,就会产生O(dL2)这个十分糟糕的结果(给10,000个样本,每个样本1000维,基本就不用算了,算不出来,呵呵,而这种输入规模对文本分类来说太正常了)。
这样再回头看就会明白为什么一对一方法尽管要训练的两类分类器数量多,但总时间实际上比一对其余方法要少了,因为一对其余方法每次训练都考虑了所有样本(只是每次把不同的部分划分为正类或者负类而已),自然慢上很多。
前文提到过,除了开方检验(CHI)以外,信息增益(IG,Information Gain)也是很有效的特征选择方法。但凡是特征选择,总是在将特征的重要程度量化之后再进行选择,而如何量化特征的重要性,就成了各种方法间最大的不同。开方检验中使用特征与类别间的关联性来进行这个量化,关联性越强,特征得分越高,该特征越应该被保留。
在信息增益中,重要性的衡量标准就是看特征能够为分类系统带来多少信息,带来的信息越多,该特征越重要。
因此先回忆一下信息论中有关信息量(就是“熵”)的定义。说有这么一个变量X,它可能的取值有n多种,分别是x1,x2,……,xn,每一种取到的概率分别是P1,P2,……,Pn,那么X的熵就定义为:
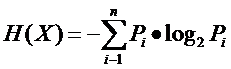
意思就是一个变量可能的变化越多(反而跟变量具体的取值没有任何关系,只和值的种类多少以及发生概率有关),它携带的信息量就越大(因此我一直觉得我们的政策法规信息量非常大,因为它变化很多,基本朝令夕改,笑)。
对分类系统来说,类别C是变量,它可能的取值是C1,C2,……,Cn,而每一个类别出现的概率是P(C1),P(C2),……,P(Cn),因此n就是类别的总数。此时分类系统的熵就可以表示为:
![clip_image002[4] clip_image002[4]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/7fce385fe28b_D158/clip_image002%5B4%5D_thumb.gif)
有同学说不好理解呀,这样想就好了,文本分类系统的作用就是输出一个表示文本属于哪个类别的值,而这个值可能是C1,C2,……,Cn,因此这个值所携带的信息量就是上式中的这么多。
信息增益是针对一个一个的特征而言的,就是看一个特征t,系统有它和没它的时候信息量各是多少,两者的差值就是这个特征给系统带来的信息量,即增益。系统含有特征t的时候信息量很好计算,就是刚才的式子,它表示的是包含所有特征时系统的信息量。
问题是当系统不包含t时,信息量如何计算?我们换个角度想问题,把系统要做的事情想象成这样:说教室里有很多座位,学生们每次上课进来的时候可以随便坐,因而变化是很大的(无数种可能的座次情况);但是现在有一个座位,看黑板很清楚,听老师讲也很清楚,于是校长的小舅子的姐姐的女儿托关系(真辗转啊),把这个座位定下来了,每次只能给她坐,别人不行,此时情况怎样?对于座次的可能情况来说,我们很容易看出以下两种情况是等价的:(1)教室里没有这个座位;(2)教室里虽然有这个座位,但其他人不能坐(因为反正它也不能参与到变化中来,它是不变的)。
对应到我们的系统中,就是下面的等价:(1)系统不包含特征t;(2)系统虽然包含特征t,但是t已经固定了,不能变化。
我们计算分类系统不包含特征t的时候,就使用情况(2)来代替,就是计算当一个特征t不能变化时,系统的信息量是多少。这个信息量其实也有专门的名称,就叫做“条件熵”,条件嘛,自然就是指“t已经固定“这个条件。
但是问题接踵而至,例如一个特征X,它可能的取值有n多种(x1,x2,……,xn),当计算条件熵而需要把它固定的时候,要把它固定在哪一个值上呢?答案是每一种可能都要固定一下,计算n个值,然后取均值才是条件熵。而取均值也不是简单的加一加然后除以n,而是要用每个值出现的概率来算平均(简单理解,就是一个值出现的可能性比较大,固定在它上面时算出来的信息量占的比重就要多一些)。
因此有这样两个条件熵的表达式:
![clip_image002[6] clip_image002[6]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/7fce385fe28b_D158/clip_image002%5B6%5D_thumb.gif)
这是指特征X被固定为值xi时的条件熵,
![clip_image002[8] clip_image002[8]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/7fce385fe28b_D158/clip_image002%5B8%5D_thumb.gif)
这是指特征X被固定时的条件熵,注意与上式在意义上的区别。从刚才计算均值的讨论可以看出来,第二个式子与第一个式子的关系就是:
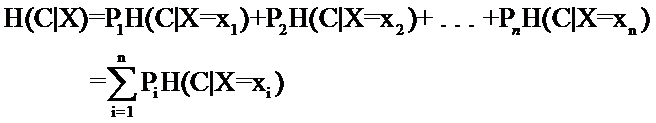
具体到我们文本分类系统中的特征t,t有几个可能的值呢?注意t是指一个固定的特征,比如他就是指关键词“经济”或者“体育”,当我们说特征“经济”可能的取值时,实际上只有两个,“经济”要么出现,要么不出现。一般的,t的取值只有t(代表t出现)和 (代表t不出现),注意系统包含t但t 不出现与系统根本不包含t可是两回事。 (代表t不出现),注意系统包含t但t 不出现与系统根本不包含t可是两回事。
因此固定t时系统的条件熵就有了,为了区别t出现时的符号与特征t本身的符号,我们用T代表特征,而用t代表T出现,那么:
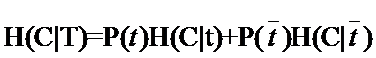
与刚才的式子对照一下,含义很清楚对吧,P(t)就是T出现的概率,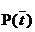 就是T不出现的概率。这个式子可以进一步展开,其中的 就是T不出现的概率。这个式子可以进一步展开,其中的
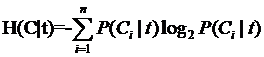
另一半就可以展开为:
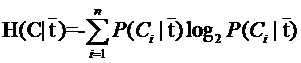
因此特征T给系统带来的信息增益就可以写成系统原本的熵与固定特征T后的条件熵之差:
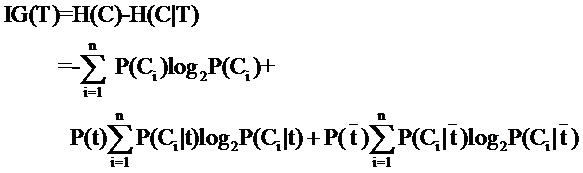
公式中的东西看上去很多,其实也都很好计算。比如P(Ci),表示类别Ci出现的概率,其实只要用1除以类别总数就得到了(这是说你平等的看待每个类别而忽略它们的大小时这样算,如果考虑了大小就要把大小的影响加进去)。再比如P(t),就是特征T出现的概率,只要用出现过T的文档数除以总文档数就可以了,再比如P(Ci|t)表示出现T的时候,类别Ci出现的概率,只要用出现了T并且属于类别Ci的文档数除以出现了T的文档数就可以了。
从以上讨论中可以看出,信息增益也是考虑了特征出现和不出现两种情况,与开方检验一样,是比较全面的,因而效果不错。但信息增益最大的问题还在于它只能考察特征对整个系统的贡献,而不能具体到某个类别上,这就使得它只适合用来做所谓“全局”的特征选择(指所有的类都使用相同的特征集合),而无法做“本地”的特征选择(每个类别有自己的特征集合,因为有的词,对这个类别很有区分度,对另一个类别则无足轻重)。
看看,导出的过程其实很简单,没有什么神秘的对不对。可有的学术论文里就喜欢把这种本来很直白的东西写得很晦涩,仿佛只有读者看不懂才是作者的真正成功。
咱们是新一代的学者,咱们没有知识不怕被别人看出来,咱们有知识也不怕教给别人。所以咱都把事情说简单点,说明白点,大家好,才是真的好。
接下来要说的东西其实不是松弛变量本身,但由于是为了使用松弛变量才引入的,因此放在这里也算合适,那就是惩罚因子C。回头看一眼引入了松弛变量以后的优化问题: 
注意其中C的位置,也可以回想一下C所起的作用(表征你有多么重视离群点,C越大越重视,越不想丢掉它们)。这个式子是以前做SVM的人写的,大家也就这么用,但没有任何规定说必须对所有的松弛变量都使用同一个惩罚因子,我们完全可以给每一个离群点都使用不同的C,这时就意味着你对每个样本的重视程度都不一样,有些样本丢了也就丢了,错了也就错了,这些就给一个比较小的C;而有些样本很重要,决不能分类错误(比如中央下达的文件啥的,笑),就给一个很大的C。 当然实际使用的时候并没有这么极端,但一种很常用的变形可以用来解决分类问题中样本的“偏斜”问题。 先来说说样本的偏斜问题,也叫数据集偏斜(unbalanced),它指的是参与分类的两个类别(也可以指多个类别)样本数量差异很大。比如说正类有10,000个样本,而负类只给了100个,这会引起的问题显而易见,可以看看下面的图: 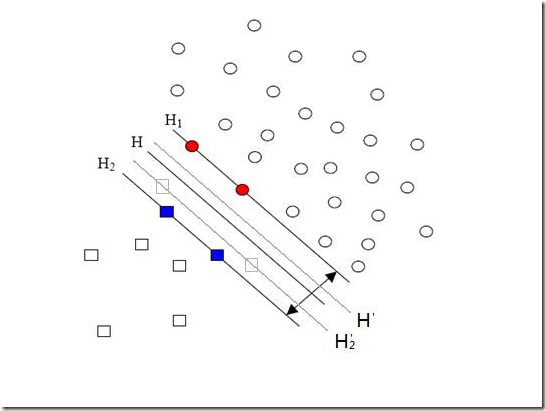 方形的点是负类。H,H1,H2是根据给的样本算出来的分类面,由于负类的样本很少很少,所以有一些本来是负类的样本点没有提供,比如图中两个灰色的方形点,如果这两个点有提供的话,那算出来的分类面应该是H’,H2’和H1,他们显然和之前的结果有出入,实际上负类给的样本点越多,就越容易出现在灰色点附近的点,我们算出的结果也就越接近于真实的分类面。但现在由于偏斜的现象存在,使得数量多的正类可以把分类面向负类的方向“推”,因而影响了结果的准确性。 对付数据集偏斜问题的方法之一就是在惩罚因子上作文章,想必大家也猜到了,那就是给样本数量少的负类更大的惩罚因子,表示我们重视这部分样本(本来数量就少,再抛弃一些,那人家负类还活不活了),因此我们的目标函数中因松弛变量而损失的部分就变成了: ![clip_image002[5] clip_image002[5]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVM_11A27/clip_image002%5B5%5D_thumb.gif)
其中i=1…p都是正样本,j=p+1…p+q都是负样本。libSVM这个算法包在解决偏斜问题的时候用的就是这种方法。 那C+和C-怎么确定呢?它们的大小是试出来的(参数调优),但是他们的比例可以有些方法来确定。咱们先假定说C+是5这么大,那确定C-的一个很直观的方法就是使用两类样本数的比来算,对应到刚才举的例子,C-就可以定为500这么大(因为10,000:100=100:1嘛)。 但是这样并不够好,回看刚才的图,你会发现正类之所以可以“欺负”负类,其实并不是因为负类样本少,真实的原因是负类的样本分布的不够广(没扩充到负类本应该有的区域)。说一个具体点的例子,现在想给政治类和体育类的文章做分类,政治类文章很多,而体育类只提供了几篇关于篮球的文章,这时分类会明显偏向于政治类,如果要给体育类文章增加样本,但增加的样本仍然全都是关于篮球的(也就是说,没有足球,排球,赛车,游泳等等),那结果会怎样呢?虽然体育类文章在数量上可以达到与政治类一样多,但过于集中了,结果仍会偏向于政治类!所以给C+和C-确定比例更好的方法应该是衡量他们分布的程度。比如可以算算他们在空间中占据了多大的体积,例如给负类找一个超球——就是高维空间里的球啦——它可以包含所有负类的样本,再给正类找一个,比比两个球的半径,就可以大致确定分布的情况。显然半径大的分布就比较广,就给小一点的惩罚因子。 但是这样还不够好,因为有的类别样本确实很集中,这不是提供的样本数量多少的问题,这是类别本身的特征(就是某些话题涉及的面很窄,例如计算机类的文章就明显不如文化类的文章那么“天马行空”),这个时候即便超球的半径差异很大,也不应该赋予两个类别不同的惩罚因子。 看到这里读者一定疯了,因为说来说去,这岂不成了一个解决不了的问题?然而事实如此,完全的方法是没有的,根据需要,选择实现简单又合用的就好(例如libSVM就直接使用样本数量的比)。
现在我们已经把一个本来线性不可分的文本分类问题,通过映射到高维空间而变成了线性可分的。就像下图这样:
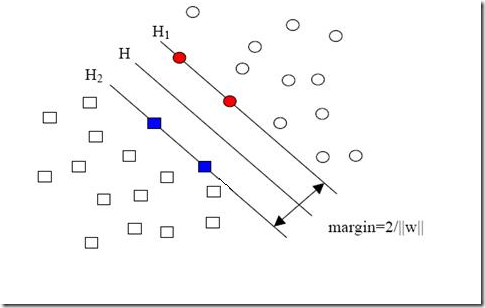
圆形和方形的点各有成千上万个(毕竟,这就是我们训练集中文档的数量嘛,当然很大了)。现在想象我们有另一个训练集,只比原先这个训练集多了一篇文章,映射到高维空间以后(当然,也使用了相同的核函数),也就多了一个样本点,但是这个样本的位置是这样的:
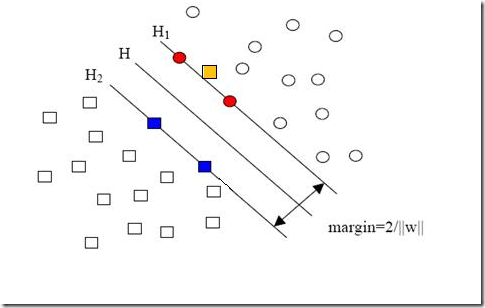
就是图中黄色那个点,它是方形的,因而它是负类的一个样本,这单独的一个样本,使得原本线性可分的问题变成了线性不可分的。这样类似的问题(仅有少数点线性不可分)叫做“近似线性可分”的问题。
以我们人类的常识来判断,说有一万个点都符合某种规律(因而线性可分),有一个点不符合,那这一个点是否就代表了分类规则中我们没有考虑到的方面呢(因而规则应该为它而做出修改)?
其实我们会觉得,更有可能的是,这个样本点压根就是错误,是噪声,是提供训练集的同学人工分类时一打瞌睡错放进去的。所以我们会简单的忽略这个样本点,仍然使用原来的分类器,其效果丝毫不受影响。
但这种对噪声的容错性是人的思维带来的,我们的程序可没有。由于我们原本的优化问题的表达式中,确实要考虑所有的样本点(不能忽略某一个,因为程序它怎么知道该忽略哪一个呢?),在此基础上寻找正负类之间的最大几何间隔,而几何间隔本身代表的是距离,是非负的,像上面这种有噪声的情况会使得整个问题无解。这种解法其实也叫做“硬间隔”分类法,因为他硬性的要求所有样本点都满足和分类平面间的距离必须大于某个值。
因此由上面的例子中也可以看出,硬间隔的分类法其结果容易受少数点的控制,这是很危险的(尽管有句话说真理总是掌握在少数人手中,但那不过是那一小撮人聊以自慰的词句罢了,咱还是得民主)。
但解决方法也很明显,就是仿照人的思路,允许一些点到分类平面的距离不满足原先的要求。由于不同的训练集各点的间距尺度不太一样,因此用间隔(而不是几何间隔)来衡量有利于我们表达形式的简洁。我们原先对样本点的要求是:
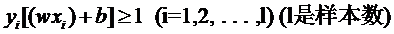
意思是说离分类面最近的样本点函数间隔也要比1大。如果要引入容错性,就给1这个硬性的阈值加一个松弛变量,即允许
![clip_image002[5] clip_image002[5]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVM_D32/clip_image002%5B5%5D_thumb.gif)
因为松弛变量是非负的,因此最终的结果是要求间隔可以比1小。但是当某些点出现这种间隔比1小的情况时(这些点也叫离群点),意味着我们放弃了对这些点的精确分类,而这对我们的分类器来说是种损失。但是放弃这些点也带来了好处,那就是使分类面不必向这些点的方向移动,因而可以得到更大的几何间隔(在低维空间看来,分类边界也更平滑)。显然我们必须权衡这种损失和好处。好处很明显,我们得到的分类间隔越大,好处就越多。回顾我们原始的硬间隔分类对应的优化问题:
![clip_image002[7] clip_image002[7]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVM_D32/clip_image002%5B7%5D_thumb.gif)
||w||2就是我们的目标函数(当然系数可有可无),希望它越小越好,因而损失就必然是一个能使之变大的量(能使它变小就不叫损失了,我们本来就希望目标函数值越小越好)。那如何来衡量损失,有两种常用的方式,有人喜欢用
![clip_image002[9] clip_image002[9]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVM_D32/clip_image002%5B9%5D_thumb.gif)
而有人喜欢用
![clip_image002[11] clip_image002[11]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVM_D32/clip_image002%5B11%5D_thumb.gif)
其中l都是样本的数目。两种方法没有大的区别。如果选择了第一种,得到的方法的就叫做二阶软间隔分类器,第二种就叫做一阶软间隔分类器。把损失加入到目标函数里的时候,就需要一个惩罚因子(cost,也就是libSVM的诸多参数中的C),原来的优化问题就变成了下面这样:
![clip_image002[13] clip_image002[13]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVM_D32/clip_image002%5B13%5D_thumb.gif)
这个式子有这么几点要注意:
一是并非所有的样本点都有一个松弛变量与其对应。实际上只有“离群点”才有,或者也可以这么看,所有没离群的点松弛变量都等于0(对负类来说,离群点就是在前面图中,跑到H2右侧的那些负样本点,对正类来说,就是跑到H1左侧的那些正样本点)。
二是松弛变量的值实际上标示出了对应的点到底离群有多远,值越大,点就越远。
三是惩罚因子C决定了你有多重视离群点带来的损失,显然当所有离群点的松弛变量的和一定时,你定的C越大,对目标函数的损失也越大,此时就暗示着你非常不愿意放弃这些离群点,最极端的情况是你把C定为无限大,这样只要稍有一个点离群,目标函数的值马上变成无限大,马上让问题变成无解,这就退化成了硬间隔问题。
四是惩罚因子C不是一个变量,整个优化问题在解的时候,C是一个你必须事先指定的值,指定这个值以后,解一下,得到一个分类器,然后用测试数据看看结果怎么样,如果不够好,换一个C的值,再解一次优化问题,得到另一个分类器,再看看效果,如此就是一个参数寻优的过程,但这和优化问题本身决不是一回事,优化问题在解的过程中,C一直是定值,要记住。
五是尽管加了松弛变量这么一说,但这个优化问题仍然是一个优化问题(汗,这不废话么),解它的过程比起原始的硬间隔问题来说,没有任何更加特殊的地方。
从大的方面说优化问题解的过程,就是先试着确定一下w,也就是确定了前面图中的三条直线,这时看看间隔有多大,又有多少点离群,把目标函数的值算一算,再换一组三条直线(你可以看到,分类的直线位置如果移动了,有些原来离群的点会变得不再离群,而有的本来不离群的点会变成离群点),再把目标函数的值算一算,如此往复(迭代),直到最终找到目标函数最小时的w。
啰嗦了这么多,读者一定可以马上自己总结出来,松弛变量也就是个解决线性不可分问题的方法罢了,但是回想一下,核函数的引入不也是为了解决线性不可分的问题么?为什么要为了一个问题使用两种方法呢?
其实两者还有微妙的不同。一般的过程应该是这样,还以文本分类为例。在原始的低维空间中,样本相当的不可分,无论你怎么找分类平面,总会有大量的离群点,此时用核函数向高维空间映射一下,虽然结果仍然是不可分的,但比原始空间里的要更加接近线性可分的状态(就是达到了近似线性可分的状态),此时再用松弛变量处理那些少数“冥顽不化”的离群点,就简单有效得多啦。
本节中的(式1)也确实是支持向量机最最常用的形式。至此一个比较完整的支持向量机框架就有了,简单说来,支持向量机就是使用了核函数的软间隔线性分类法。
下一节会说说松弛变量剩下的一点点东西,顺便搞个读者调查,看看大家还想侃侃SVM的哪些方面。
生存?还是毁灭?——哈姆雷特
可分?还是不可分?——支持向量机
之前一直在讨论的线性分类器,器如其名(汗,这是什么说法啊),只能对线性可分的样本做处理。如果提供的样本线性不可分,结果很简单,线性分类器的求解程序会无限循环,永远也解不出来。这必然使得它的适用范围大大缩小,而它的很多优点我们实在不原意放弃,怎么办呢?是否有某种方法,让线性不可分的数据变得线性可分呢?
有!其思想说来也简单,来用一个二维平面中的分类问题作例子,你一看就会明白。事先声明,下面这个例子是网络早就有的,我一时找不到原作者的正确信息,在此借用,并加进了我自己的解说而已。
例子是下面这张图:
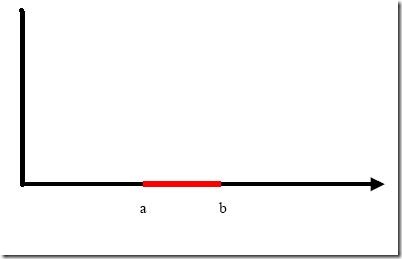
我们把横轴上端点a和b之间红色部分里的所有点定为正类,两边的黑色部分里的点定为负类。试问能找到一个线性函数把两类正确分开么?不能,因为二维空间里的线性函数就是指直线,显然找不到符合条件的直线。
但我们可以找到一条曲线,例如下面这一条:
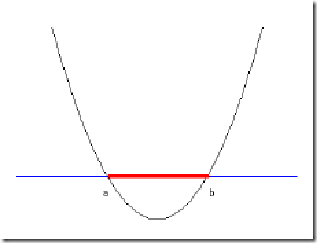
显然通过点在这条曲线的上方还是下方就可以判断点所属的类别(你在横轴上随便找一点,算算这一点的函数值,会发现负类的点函数值一定比0大,而正类的一定比0小)。这条曲线就是我们熟知的二次曲线,它的函数表达式可以写为:
![clip_image002[5] clip_image002[5]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVM_10595/clip_image002%5B5%5D_thumb.gif)
问题只是它不是一个线性函数,但是,下面要注意看了,新建一个向量y和a:
![clip_image002[7] clip_image002[7]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVM_10595/clip_image002%5B7%5D_thumb.gif)
这样g(x)就可以转化为f(y)=<a,y>,你可以把y和a分别回带一下,看看等不等于原来的g(x)。用内积的形式写你可能看不太清楚,实际上f(y)的形式就是:
g(x)=f(y)=ay
在任意维度的空间中,这种形式的函数都是一个线性函数(只不过其中的a和y都是多维向量罢了),因为自变量y的次数不大于1。
看出妙在哪了么?原来在二维空间中一个线性不可分的问题,映射到四维空间后,变成了线性可分的!因此这也形成了我们最初想解决线性不可分问题的基本思路——向高维空间转化,使其变得线性可分。
而转化最关键的部分就在于找到x到y的映射方法。遗憾的是,如何找到这个映射,没有系统性的方法(也就是说,纯靠猜和凑)。具体到我们的文本分类问题,文本被表示为上千维的向量,即使维数已经如此之高,也常常是线性不可分的,还要向更高的空间转化。其中的难度可想而知。
小Tips:为什么说f(y)=ay是四维空间里的函数?
大家可能一时没看明白。回想一下我们二维空间里的函数定义
g(x)=ax+b
变量x是一维的,为什么说它是二维空间里的函数呢?因为还有一个变量我们没写出来,它的完整形式其实是
y=g(x)=ax+b
即
y=ax+b
看看,有几个变量?两个。那是几维空间的函数?(作者五岁的弟弟答:五维的。作者:……)
再看看
f(y)=ay
里面的y是三维的变量,那f(y)是几维空间里的函数?(作者五岁的弟弟答:还是五维的。作者:……)
用一个具体文本分类的例子来看看这种向高维空间映射从而分类的方法如何运作,想象一下,我们文本分类问题的原始空间是1000维的(即每个要被分类的文档被表示为一个1000维的向量),在这个维度上问题是线性不可分的。现在我们有一个2000维空间里的线性函数
f(x’)=<w’,x’>+b
注意向量的右上角有个 ’哦。它能够将原问题变得可分。式中的 w’和x’都是2000维的向量,只不过w’是定值,而x’是变量(好吧,严格说来这个函数是2001维的,哈哈),现在我们的输入呢,是一个1000维的向量x,分类的过程是先把x变换为2000维的向量x’,然后求这个变换后的向量x’与向量w’的内积,再把这个内积的值和b相加,就得到了结果,看结果大于阈值还是小于阈值就得到了分类结果。
你发现了什么?我们其实只关心那个高维空间里内积的值,那个值算出来了,分类结果就算出来了。而从理论上说, x’是经由x变换来的,因此广义上可以把它叫做x的函数(有一个x,就确定了一个x’,对吧,确定不出第二个),而w’是常量,它是一个低维空间里的常量w经过变换得到的,所以给了一个w 和x的值,就有一个确定的f(x’)值与其对应。这让我们幻想,是否能有这样一种函数K(w,x),他接受低维空间的输入值,却能算出高维空间的内积值<w’,x’>?
如果有这样的函数,那么当给了一个低维空间的输入x以后,
g(x)=K(w,x)+b
f(x’)=<w’,x’>+b
这两个函数的计算结果就完全一样,我们也就用不着费力找那个映射关系,直接拿低维的输入往g(x)里面代就可以了(再次提醒,这回的g(x)就不是线性函数啦,因为你不能保证K(w,x)这个表达式里的x次数不高于1哦)。
万幸的是,这样的K(w,x)确实存在(发现凡是我们人类能解决的问题,大都是巧得不能再巧,特殊得不能再特殊的问题,总是恰好有些能投机取巧的地方才能解决,由此感到人类的渺小),它被称作核函数(核,kernel),而且还不止一个,事实上,只要是满足了Mercer条件的函数,都可以作为核函数。核函数的基本作用就是接受两个低维空间里的向量,能够计算出经过某个变换后在高维空间里的向量内积值。几个比较常用的核函数,俄,教课书里都列过,我就不敲了(懒!)。
回想我们上节说的求一个线性分类器,它的形式应该是:
![clip_image002[9] clip_image002[9]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVM_10595/clip_image002%5B9%5D_thumb.gif)
现在这个就是高维空间里的线性函数(为了区别低维和高维空间里的函数和向量,我改了函数的名字,并且给w和x都加上了 ’),我们就可以用一个低维空间里的函数(再一次的,这个低维空间里的函数就不再是线性的啦)来代替,
![clip_image002[11] clip_image002[11]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVM_10595/clip_image002%5B11%5D_thumb.gif)
又发现什么了?f(x’) 和g(x)里的α,y,b全都是一样一样的!这就是说,尽管给的问题是线性不可分的,但是我们就硬当它是线性问题来求解,只不过求解过程中,凡是要求内积的时候就用你选定的核函数来算。这样求出来的α再和你选定的核函数一组合,就得到分类器啦!
明白了以上这些,会自然的问接下来两个问题:
1. 既然有很多的核函数,针对具体问题该怎么选择?
2. 如果使用核函数向高维空间映射后,问题仍然是线性不可分的,那怎么办?
第一个问题现在就可以回答你:对核函数的选择,现在还缺乏指导原则!各种实验的观察结果(不光是文本分类)的确表明,某些问题用某些核函数效果很好,用另一些就很差,但是一般来讲,径向基核函数是不会出太大偏差的一种,首选。(我做文本分类系统的时候,使用径向基核函数,没有参数调优的情况下,绝大部分类别的准确和召回都在85%以上,可见。虽然libSVM的作者林智仁认为文本分类用线性核函数效果更佳,待考证)
对第二个问题的解决则引出了我们下一节的主题:松弛变量。
让我再一次比较完整的重复一下我们要解决的问题:我们有属于两个类别的样本点(并不限定这些点在二维空间中)若干,如图,
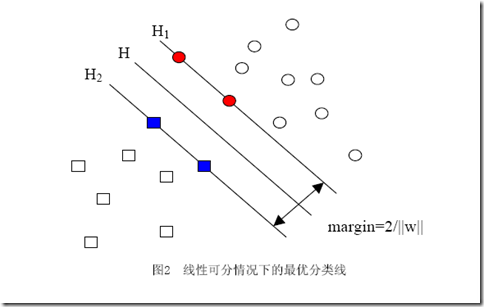
圆形的样本点定为正样本(连带着,我们可以把正样本所属的类叫做正类),方形的点定为负例。我们想求得这样一个线性函数(在n维空间中的线性函数):
g(x)=wx+b
使得所有属于正类的点x+代入以后有g(x+)≥1,而所有属于负类的点x-代入后有g(x-)≤-1(之所以总跟1比较,无论正一还是负一,都是因为我们固定了间隔为1,注意间隔和几何间隔的区别)。代入g(x)后的值如果在1和-1之间,我们就拒绝判断。
求这样的g(x)的过程就是求w(一个n维向量)和b(一个实数)两个参数的过程(但实际上只需要求w,求得以后找某些样本点代入就可以求得b)。因此在求g(x)的时候,w才是变量。
你肯定能看出来,一旦求出了w(也就求出了b),那么中间的直线H就知道了(因为它就是wx+b=0嘛,哈哈),那么H1和H2也就知道了(因为三者是平行的,而且相隔的距离还是||w||决定的)。那么w是谁决定的?显然是你给的样本决定的,一旦你在空间中给出了那些个样本点,三条直线的位置实际上就唯一确定了(因为我们求的是最优的那三条,当然是唯一的),我们解优化问题的过程也只不过是把这个确定了的东西算出来而已。
样本确定了w,用数学的语言描述,就是w可以表示为样本的某种组合:
w=α1x1+α2x2+…+αnxn
式子中的αi是一个一个的数(在严格的证明过程中,这些α被称为拉格朗日乘子),而xi是样本点,因而是向量,n就是总样本点的个数。为了方便描述,以下开始严格区别数字与向量的乘积和向量间的乘积,我会用α1x1表示数字和向量的乘积,而用<x1,x2>表示向量x1,x2的内积(也叫点积,注意与向量叉积的区别)。因此g(x)的表达式严格的形式应该是:
g(x)=<w,x>+b
但是上面的式子还不够好,你回头看看图中正样本和负样本的位置,想像一下,我不动所有点的位置,而只是把其中一个正样本点定为负样本点(也就是把一个点的形状从圆形变为方形),结果怎么样?三条直线都必须移动(因为对这三条直线的要求是必须把方形和圆形的点正确分开)!这说明w不仅跟样本点的位置有关,还跟样本的类别有关(也就是和样本的“标签”有关)。因此用下面这个式子表示才算完整:
w=α1y1x1+α2y2x2+…+αnynxn (式1)
其中的yi就是第i个样本的标签,它等于1或者-1。其实以上式子的那一堆拉格朗日乘子中,只有很少的一部分不等于0(不等于0才对w起决定作用),这部分不等于0的拉格朗日乘子后面所乘的样本点,其实都落在H1和H2上,也正是这部分样本(而不需要全部样本)唯一的确定了分类函数,当然,更严格的说,这些样本的一部分就可以确定,因为例如确定一条直线,只需要两个点就可以,即便有三五个都落在上面,我们也不是全都需要。这部分我们真正需要的样本点,就叫做支持(撑)向量!(名字还挺形象吧,他们“撑”起了分界线)
式子也可以用求和符号简写一下:
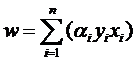
因此原来的g(x)表达式可以写为:
![clip_image002[4] clip_image002[4]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVM_1244A/clip_image002%5B4%5D_thumb.gif)
注意式子中x才是变量,也就是你要分类哪篇文档,就把该文档的向量表示代入到 x的位置,而所有的xi统统都是已知的样本。还注意到式子中只有xi和x是向量,因此一部分可以从内积符号中拿出来,得到g(x)的式子为:
![clip_image002[6] clip_image002[6]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVM_1244A/clip_image002%5B6%5D_thumb.gif)
发现了什么?w不见啦!从求w变成了求α。
但肯定有人会说,这并没有把原问题简化呀。嘿嘿,其实简化了,只不过在你看不见的地方,以这样的形式描述问题以后,我们的优化问题少了很大一部分不等式约束(记得这是我们解不了极值问题的万恶之源)。但是接下来先跳过线性分类器求解的部分,来看看 SVM在线性分类器上所做的重大改进——核函数。
从最一般的定义上说,一个求最小值的问题就是一个优化问题(也叫寻优问题,更文绉绉的叫法是规划——Programming),它同样由两部分组成,目标函数和约束条件,可以用下面的式子表示:
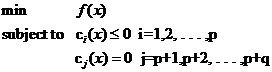 (式1) (式1)
约束条件用函数c来表示,就是constrain的意思啦。你可以看出一共有p+q个约束条件,其中p个是不等式约束,q个等式约束。
关于这个式子可以这样来理解:式中的x是自变量,但不限定它的维数必须为1(视乎你解决的问题空间维数,对我们的文本分类来说,那可是成千上万啊)。要求f(x)在哪一点上取得最小值(反倒不太关心这个最小值到底是多少,关键是哪一点),但不是在整个空间里找,而是在约束条件所划定的一个有限的空间里找,这个有限的空间就是优化理论里所说的可行域。注意可行域中的每一个点都要求满足所有p+q个条件,而不是满足其中一条或几条就可以(切记,要满足每个约束),同时可行域边界上的点有一个额外好的特性,它们可以使不等式约束取得等号!而边界内的点不行。
关于可行域还有个概念不得不提,那就是凸集,凸集是指有这么一个点的集合,其中任取两个点连一条直线,这条线上的点仍然在这个集合内部,因此说“凸”是很形象的(一个反例是,二维平面上,一个月牙形的区域就不是凸集,你随便就可以找到两个点违反了刚才的规定)。
回头再来看我们线性分类器问题的描述,可以看出更多的东西。
![clip_image002[5] clip_image002[5]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVMPart2_1603/clip_image002%5B5%5D_thumb.gif) (式2) (式2)
在这个问题中,自变量就是w,而目标函数是w的二次函数,所有的约束条件都是w的线性函数(哎,千万不要把xi当成变量,它代表样本,是已知的),这种规划问题有个很有名气的称呼——二次规划(Quadratic Programming,QP),而且可以更进一步的说,由于它的可行域是一个凸集,因此它是一个凸二次规划。
一下子提了这么多术语,实在不是为了让大家以后能向别人炫耀学识的渊博,这其实是我们继续下去的一个重要前提,因为在动手求一个问题的解之前(好吧,我承认,是动计算机求……),我们必须先问自己:这个问题是不是有解?如果有解,是否能找到?
对于一般意义上的规划问题,两个问题的答案都是不一定,但凸二次规划让人喜欢的地方就在于,它有解(教科书里面为了严谨,常常加限定成分,说它有全局最优解,由于我们想找的本来就是全局最优的解,所以不加也罢),而且可以找到!(当然,依据你使用的算法不同,找到这个解的速度,行话叫收敛速度,会有所不同)
对比(式2)和(式1)还可以发现,我们的线性分类器问题只有不等式约束,因此形式上看似乎比一般意义上的规划问题要简单,但解起来却并非如此。
因为我们实际上并不知道该怎么解一个带约束的优化问题。如果你仔细回忆一下高等数学的知识,会记得我们可以轻松的解一个不带任何约束的优化问题(实际上就是当年背得烂熟的函数求极值嘛,求导再找0点呗,谁不会啊?笑),我们甚至还会解一个只带等式约束的优化问题,也是背得烂熟的,求条件极值,记得么,通过添加拉格朗日乘子,构造拉格朗日函数,来把这个问题转化为无约束的优化问题云云(如果你一时没想通,我提醒一下,构造出的拉格朗日函数就是转化之后的问题形式,它显然没有带任何条件)。
读者问:如果只带等式约束的问题可以转化为无约束的问题而得以求解,那么可不可以把带不等式约束的问题向只带等式约束的问题转化一下而得以求解呢?
聪明,可以,实际上我们也正是这么做的。下一节就来说说如何做这个转化,一旦转化完成,求解对任何学过高等数学的人来说,都是小菜一碟啦。
上节说到我们有了一个线性分类函数,也有了判断解优劣的标准——即有了优化的目标,这个目标就是最大化几何间隔,但是看过一些关于SVM的论文的人一定记得什么优化的目标是要最小化||w||这样的说法,这是怎么回事呢?回头再看看我们对间隔和几何间隔的定义:
间隔:δ=y(wx+b)=|g(x)|
几何间隔:
可以看出δ=||w||δ几何。注意到几何间隔与||w||是成反比的,因此最大化几何间隔与最小化||w||完全是一回事。而我们常用的方法并不是固定||w||的大小而寻求最大几何间隔,而是固定间隔(例如固定为1),寻找最小的||w||。
而凡是求一个函数的最小值(或最大值)的问题都可以称为寻优问题(也叫作一个规划问题),又由于找最大值的问题总可以通过加一个负号变为找最小值的问题,因此我们下面讨论的时候都针对找最小值的过程来进行。一个寻优问题最重要的部分是目标函数,顾名思义,就是指寻优的目标。例如我们想寻找最小的||w||这件事,就可以用下面的式子表示:
![clip_image002[4] clip_image002[4]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVMPart1_EEC8/clip_image002%5B4%5D_thumb.gif)
但实际上对于这个目标,我们常常使用另一个完全等价的目标函数来代替,那就是:
![clip_image002[6] clip_image002[6]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVMPart1_EEC8/clip_image002%5B6%5D_thumb.gif) (式1) (式1)
不难看出当||w||2达到最小时,||w||也达到最小,反之亦然(前提当然是||w||描述的是向量的长度,因而是非负的)。之所以采用这种形式,是因为后面的求解过程会对目标函数作一系列变换,而式(1)的形式会使变换后的形式更为简洁(正如聪明的读者所料,添加的系数二分之一和平方,皆是为求导数所需)。
接下来我们自然会问的就是,这个式子是否就描述了我们的问题呢?(回想一下,我们的问题是有一堆点,可以被分成两类,我们要找出最好的分类面)
如果直接来解这个求最小值问题,很容易看出当||w||=0的时候就得到了目标函数的最小值。但是你也会发现,无论你给什么样的数据,都是这个解!反映在图中,就是H1与H2两条直线间的距离无限大,这个时候,所有的样本点(无论正样本还是负样本)都跑到了H1和H2中间,而我们原本的意图是,H1右侧的被分为正类,H2 左侧的被分为负类,位于两类中间的样本则拒绝分类(拒绝分类的另一种理解是分给哪一类都有道理,因而分给哪一类也都没有道理)。这下可好,所有样本点都进入了无法分类的灰色地带。
造成这种结果的原因是在描述问题的时候只考虑了目标,而没有加入约束条件,约束条件就是在求解过程中必须满足的条件,体现在我们的问题中就是样本点必须在H1或H2的某一侧(或者至少在H1和H2上),而不能跑到两者中间。我们前文提到过把间隔固定为1,这是指把所有样本点中间隔最小的那一点的间隔定为1(这也是集合的间隔的定义,有点绕嘴),也就意味着集合中的其他点间隔都不会小于1,按照间隔的定义,满足这些条件就相当于让下面的式子总是成立:
yi[(w·xi)+b]≥1 (i=1,2,…,l) (l是总的样本数)
但我们常常习惯让式子的值和0比较,因而经常用变换过的形式:
yi[(w·xi)+b]-1≥0 (i=1,2,…,l) (l是总的样本数)
因此我们的两类分类问题也被我们转化成了它的数学形式,一个带约束的最小值的问题:
![clip_image002[10] clip_image002[10]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVMPart1_EEC8/clip_image002%5B10%5D_thumb.gif)
下一节我们从最一般的意义上看看一个求最小值的问题有何特征,以及如何来解。
按:之前的文章重新汇编一下,修改了一些错误和不当的说法,一起复习,然后继续SVM之旅.
(一)SVM的八股简介
支持向量机(Support Vector Machine)是Cortes和Vapnik于1995年首先提出的,它在解决小样本、非线性及高维模式识别中表现出许多特有的优势,并能够推广应用到函数拟合等其他机器学习问题中[10]。
支持向量机方法是建立在统计学习理论的VC 维理论和结构风险最小原理基础上的,根据有限的样本信息在模型的复杂性(即对特定训练样本的学习精度,Accuracy)和学习能力(即无错误地识别任意样本的能力)之间寻求最佳折衷,以期获得最好的推广能力[14](或称泛化能力)。
以上是经常被有关SVM 的学术文献引用的介绍,有点八股,我来逐一分解并解释一下。
Vapnik是统计机器学习的大牛,这想必都不用说,他出版的《Statistical Learning Theory》是一本完整阐述统计机器学习思想的名著。在该书中详细的论证了统计机器学习之所以区别于传统机器学习的本质,就在于统计机器学习能够精确的给出学习效果,能够解答需要的样本数等等一系列问题。与统计机器学习的精密思维相比,传统的机器学习基本上属于摸着石头过河,用传统的机器学习方法构造分类系统完全成了一种技巧,一个人做的结果可能很好,另一个人差不多的方法做出来却很差,缺乏指导和原则。
所谓VC维是对函数类的一种度量,可以简单的理解为问题的复杂程度,VC维越高,一个问题就越复杂。正是因为SVM关注的是VC维,后面我们可以看到,SVM解决问题的时候,和样本的维数是无关的(甚至样本是上万维的都可以,这使得SVM很适合用来解决文本分类的问题,当然,有这样的能力也因为引入了核函数)。
结构风险最小听上去文绉绉,其实说的也无非是下面这回事。
机器学习本质上就是一种对问题真实模型的逼近(我们选择一个我们认为比较好的近似模型,这个近似模型就叫做一个假设),但毫无疑问,真实模型一定是不知道的(如果知道了,我们干吗还要机器学习?直接用真实模型解决问题不就可以了?对吧,哈哈)既然真实模型不知道,那么我们选择的假设与问题真实解之间究竟有多大差距,我们就没法得知。比如说我们认为宇宙诞生于150亿年前的一场大爆炸,这个假设能够描述很多我们观察到的现象,但它与真实的宇宙模型之间还相差多少?谁也说不清,因为我们压根就不知道真实的宇宙模型到底是什么。
这个与问题真实解之间的误差,就叫做风险(更严格的说,误差的累积叫做风险)。我们选择了一个假设之后(更直观点说,我们得到了一个分类器以后),真实误差无从得知,但我们可以用某些可以掌握的量来逼近它。最直观的想法就是使用分类器在样本数据上的分类的结果与真实结果(因为样本是已经标注过的数据,是准确的数据)之间的差值来表示。这个差值叫做经验风险Remp(w)。以前的机器学习方法都把经验风险最小化作为努力的目标,但后来发现很多分类函数能够在样本集上轻易达到100%的正确率,在真实分类时却一塌糊涂(即所谓的推广能力差,或泛化能力差)。此时的情况便是选择了一个足够复杂的分类函数(它的VC维很高),能够精确的记住每一个样本,但对样本之外的数据一律分类错误。回头看看经验风险最小化原则我们就会发现,此原则适用的大前提是经验风险要确实能够逼近真实风险才行(行话叫一致),但实际上能逼近么?答案是不能,因为样本数相对于现实世界要分类的文本数来说简直九牛一毛,经验风险最小化原则只在这占很小比例的样本上做到没有误差,当然不能保证在更大比例的真实文本上也没有误差。
统计学习因此而引入了泛化误差界的概念,就是指真实风险应该由两部分内容刻画,一是经验风险,代表了分类器在给定样本上的误差;二是置信风险,代表了我们在多大程度上可以信任分类器在未知文本上分类的结果。很显然,第二部分是没有办法精确计算的,因此只能给出一个估计的区间,也使得整个误差只能计算上界,而无法计算准确的值(所以叫做泛化误差界,而不叫泛化误差)。
置信风险与两个量有关,一是样本数量,显然给定的样本数量越大,我们的学习结果越有可能正确,此时置信风险越小;二是分类函数的VC维,显然VC维越大,推广能力越差,置信风险会变大。
泛化误差界的公式为:
R(w)≤Remp(w)+Ф(n/h)
公式中R(w)就是真实风险,Remp(w)就是经验风险,Ф(n/h)就是置信风险。统计学习的目标从经验风险最小化变为了寻求经验风险与置信风险的和最小,即结构风险最小。
SVM正是这样一种努力最小化结构风险的算法。
SVM其他的特点就比较容易理解了。
小样本,并不是说样本的绝对数量少(实际上,对任何算法来说,更多的样本几乎总是能带来更好的效果),而是说与问题的复杂度比起来,SVM算法要求的样本数是相对比较少的。
非线性,是指SVM擅长应付样本数据线性不可分的情况,主要通过松弛变量(也有人叫惩罚变量)和核函数技术来实现,这一部分是SVM的精髓,以后会详细讨论。多说一句,关于文本分类这个问题究竟是不是线性可分的,尚没有定论,因此不能简单的认为它是线性可分的而作简化处理,在水落石出之前,只好先当它是线性不可分的(反正线性可分也不过是线性不可分的一种特例而已,我们向来不怕方法过于通用)。
高维模式识别是指样本维数很高,例如文本的向量表示,如果没有经过另一系列文章(《文本分类入门》)中提到过的降维处理,出现几万维的情况很正常,其他算法基本就没有能力应付了,SVM却可以,主要是因为SVM 产生的分类器很简洁,用到的样本信息很少(仅仅用到那些称之为“支持向量”的样本,此为后话),使得即使样本维数很高,也不会给存储和计算带来大麻烦(相对照而言,kNN算法在分类时就要用到所有样本,样本数巨大,每个样本维数再一高,这日子就没法过了……)。
下一节开始正式讨论SVM。别嫌我说得太详细哦。
SVM入门(二)线性分类器Part 1
线性分类器(一定意义上,也可以叫做感知机) 是最简单也很有效的分类器形式.在一个线性分类器中,可以看到SVM形成的思路,并接触很多SVM的核心概念.
用一个二维空间里仅有两类样本的分类问题来举个小例子。如图所示
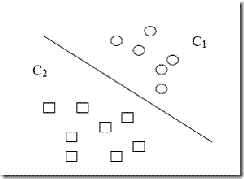
C1和C2是要区分的两个类别,在二维平面中它们的样本如上图所示。中间的直线就是一个分类函数,它可以将两类样本完全分开。一般的,如果一个线性函数能够将样本完全正确的分开,就称这些数据是线性可分的,否则称为非线性可分的。
什么叫线性函数呢?在一维空间里就是一个点,在二维空间里就是一条直线,三维空间里就是一个平面,可以如此想象下去,如果不关注空间的维数,这种线性函数还有一个统一的名称——超平面(Hyper Plane)!
实际上,一个线性函数是一个实值函数(即函数的值是连续的实数),而我们的分类问题(例如这里的二元分类问题——回答一个样本属于还是不属于一个类别的问题)需要离散的输出值,例如用1表示某个样本属于类别C1,而用0表示不属于(不属于C1也就意味着属于C2),这时候只需要简单的在实值函数的基础上附加一个阈值即可,通过分类函数执行时得到的值大于还是小于这个阈值来确定类别归属。 例如我们有一个线性函数
g(x)=wx+b
我们可以取阈值为0,这样当有一个样本xi需要判别的时候,我们就看g(xi)的值。若g(xi)>0,就判别为类别C1,若g(xi)<0,则判别为类别C2(等于的时候我们就拒绝判断,呵呵)。此时也等价于给函数g(x)附加一个符号函数sgn(),即f(x)=sgn [g(x)]是我们真正的判别函数。
关于g(x)=wx+b这个表达式要注意三点:一,式中的x不是二维坐标系中的横轴,而是样本的向量表示,例如一个样本点的坐标是(3,8),则xT=(3,8) ,而不是x=3(一般说向量都是说列向量,因此以行向量形式来表示时,就加上转置)。二,这个形式并不局限于二维的情况,在n维空间中仍然可以使用这个表达式,只是式中的w成为了n维向量(在二维的这个例子中,w是二维向量,为了表示起来方便简洁,以下均不区别列向量和它的转置,聪明的读者一看便知);三,g(x)不是中间那条直线的表达式,中间那条直线的表达式是g(x)=0,即wx+b=0,我们也把这个函数叫做分类面。
实际上很容易看出来,中间那条分界线并不是唯一的,我们把它稍微旋转一下,只要不把两类数据分错,仍然可以达到上面说的效果,稍微平移一下,也可以。此时就牵涉到一个问题,对同一个问题存在多个分类函数的时候,哪一个函数更好呢?显然必须要先找一个指标来量化“好”的程度,通常使用的都是叫做“分类间隔”的指标。下一节我们就仔细说说分类间隔,也补一补相关的数学知识。
SVM入门(三)线性分类器Part 2
上回说到对于文本分类这样的不适定问题(有一个以上解的问题称为不适定问题),需要有一个指标来衡量解决方案(即我们通过训练建立的分类模型)的好坏,而分类间隔是一个比较好的指标。
在进行文本分类的时候,我们可以让计算机这样来看待我们提供给它的训练样本,每一个样本由一个向量(就是那些文本特征所组成的向量)和一个标记(标示出这个样本属于哪个类别)组成。如下:
Di=(xi,yi)
xi就是文本向量(维数很高),yi就是分类标记。
在二元的线性分类中,这个表示分类的标记只有两个值,1和-1(用来表示属于还是不属于这个类)。有了这种表示法,我们就可以定义一个样本点到某个超平面的间隔:
δi=yi(wxi+b)
这个公式乍一看没什么神秘的,也说不出什么道理,只是个定义而已,但我们做做变换,就能看出一些有意思的东西。
首先注意到如果某个样本属于该类别的话,那么wxi+b>0(记得么?这是因为我们所选的g(x)=wx+b就通过大于0还是小于0来判断分类),而yi也大于0;若不属于该类别的话,那么wxi+b<0,而yi也小于0,这意味着yi(wxi+b)总是大于0的,而且它的值就等于|wxi+b|!(也就是|g(xi)|)
现在把w和b进行一下归一化,即用w/||w||和b/||w||分别代替原来的w和b,那么间隔就可以写成
![clip_image002[28]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVMPart2_C019/clip_image002%5B28%5D_thumb.gif)
这个公式是不是看上去有点眼熟?没错,这不就是解析几何中点xi到直线g(x)=0的距离公式嘛!(推广一下,是到超平面g(x)=0的距离, g(x)=0就是上节中提到的分类超平面)
小Tips:||w||是什么符号?||w||叫做向量w的范数,范数是对向量长度的一种度量。我们常说的向量长度其实指的是它的2-范数,范数最一般的表示形式为p-范数,可以写成如下表达式
向量w=(w1, w2, w3,…… wn)
它的p-范数为
![clip_image004[10]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVMPart2_C019/clip_image004%5B10%5D_thumb.gif)
看看把p换成2的时候,不就是传统的向量长度么?当我们不指明p的时候,就像||w||这样使用时,就意味着我们不关心p的值,用几范数都可以;或者上文已经提到了p的值,为了叙述方便不再重复指明。
当用归一化的w和b代替原值之后的间隔有一个专门的名称,叫做几何间隔,几何间隔所表示的正是点到超平面的欧氏距离,我们下面就简称几何间隔为“距离”。以上是单个点到某个超平面的距离(就是间隔,后面不再区别这两个词)定义,同样可以定义一个点的集合(就是一组样本)到某个超平面的距离为此集合中离超平面最近的点的距离。下面这张图更加直观的展示出了几何间隔的现实含义:
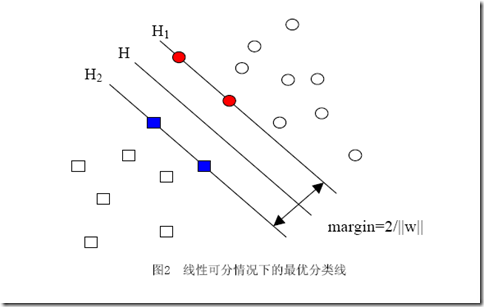
H是分类面,而H1和H2是平行于H,且过离H最近的两类样本的直线,H1与H,H2与H之间的距离就是几何间隔。
之所以如此关心几何间隔这个东西,是因为几何间隔与样本的误分次数间存在关系:

其中的δ是样本集合到分类面的间隔,R=max ||xi|| i=1,...,n,即R是所有样本中(xi是以向量表示的第i个样本)向量长度最长的值(也就是说代表样本的分布有多么广)。先不必追究误分次数的具体定义和推导过程,只要记得这个误分次数一定程度上代表分类器的误差。而从上式可以看出,误分次数的上界由几何间隔决定!(当然,是样本已知的时候)
至此我们就明白为何要选择几何间隔来作为评价一个解优劣的指标了,原来几何间隔越大的解,它的误差上界越小。因此最大化几何间隔成了我们训练阶段的目标,而且,与二把刀作者所写的不同,最大化分类间隔并不是SVM的专利,而是早在线性分类时期就已有的思想。
简单的说,比较两个int型或long型的数据没有什么问题,可以用==来判断,但对浮点数(float与double)来说,需要对Float.NaN和0.0这个两个特殊数字作额外的处理。
Float.NaN严格说来不是一个数字(它的字面意思也就是Not a Number),但是因为这个值可以被保存在一个float型的变量中(因为它常常是除0的结果),所以暂且当它是个数字吧。但它与一般的浮点数有些许不同,就是两个NaN用==比较的结果会得到false。
可以用下面的代码验证:
float nan=Float.NaN;
float anotherNan=Float.NaN;
System.out.println(nan==anotherNan);
输出结果为false
我用另一种除0的方法得到NaN,可以看到使用==判断仍然得到false。代码如下:
float overFlow=0.0f/0.0f;
System.out.println(overFlow);
System.out.println(nan==overFlow);
而当我们使用Float.compare()这个方法来比较两个NaN时,却会得到相等的结果。可以用下面的代码验证:
System.out.println(Float.compare(nan,anotherNan));
System.out.println(Float.compare(nan,overFlow));
compare()方法如果返回0,就说明两个数相等,返回-1,就说明第一个比第二个小,返回1则正好相反。
上面这两行语句的返回结果都是0。
一般来说,基本类型的compare()方法与直接使用==的效果“应该”是一样的,但在NaN这个问题上不一致,是利是弊,取决于使用的人作何期望。当程序的语义要求两个NaN不应该被认为相等时(例如用NaN来代表两个无穷大,学过高等数学的朋友们都记得,两个无穷看上去符号是一样,但不应该认为是相等的两样东西),就使用==判断;如果NaN被看得无足轻重(毕竟,我只关心数字,两个不是数字的东西就划归同一类好了嘛)就使用Float.compare()。
另一个在==和compare()方法上表现不一致的浮点数就是正0和负0(当然这也是计算机表示有符号数字的老大难问题),我们(万能的)人类当然知道0.0f和-0.0f应该是相等的数字,但是试试下面的代码:
float negZero=-0.0f;
float zero=0.0f;
System.out.println(zero==negZero);
System.out.println(Float.compare(zero,negZero));
返回的结果是true和-1。看到了么,==认为正0和负0相等,而compare()方法认为正0比负0要大。所以对0的比较来说,==是更好的选择。
目前为止不管后台写了多少逻辑(已经登录了Google,取了相册数据),我们的Gadget都还是那个看上去白白的Gadget。而要想让它看上去有所不同,就要在main.xml这个文件中,制定我们想要的“长相”(就跟征婚启事里写的一样,身高1米6至1米7,体重不超过55公斤,相貌端正,贤良淑惠)。
如果你已经下载了我提供的源码,就可以打开看看,对照实际效果来看代码,应该很好理解。我们总计在界面上放了几样东西:
- 一张背景图(就是白白的那个)
- 一张Picasa的Logo
- 两行表示欢迎的文字(就是label啦)
- 一个用来显示相册信息的列表(listbox),当然,目前列表中还一个列表项都没有(列表项称之为item)
- 最后又贴了两张图,其中一张是某企业的logo(笑)
其中值得注意的事情有这么几件:
一是背景图片绝非可有可无,按google的说法,像label这种东西,如果没有放在一张背景图片之上的话,是显示不出来的。
二是Gadget中界面的内容,样式和布局都在这一个文件中指定。
三是Gadget的界面没有HTML那种流动布局的效果,就是说,所有要显示的元素,必须明明白白的指出它的位置,也就是每个元素的x和y属性,是从该元素的父元素左上角开始计算的坐标。如果你先写了一个label(拿label举个例子,实际上用什么效果都是一样的),再挨着它写了一个label,两个label你都没有指定x和y的值,那么这个两个label会重叠着显示在一起。不信你可以试一试。
四是图片的源文件位置,从代码中可以看到指定本机上的相对目录是可以的,那么指定一个网络上的url可以么?例如http://www.sina.com.cn/images/logo.gif?如果你头脑中还存在着HTML的印象,可能想当然的以为可以这么做,而事实上不行,Gadget与Web没有天然的联系(没记错的话,我已经说过四次了)。后面处理相册缩略图的时候,我们会看到怎么把网络上的图片显示出来。
写过图形用户界面程序的人一定想问,如何让界面上的元素与代码产生联系呢?例如我们的列表,我想在代码中对它作些修改的时候,如何取得它的引用呢?在Gadget中这一点还比较方便,主要有两个途径:一是只要你给元素赋了name属性,例如我就给列表项起了一个名字叫做contentListBox,在main.xml中的这一行:
<listbox height="130" name="contentListBox" width="200" x="25" y="100"
之后就可以直接在代码中用contentListBox这个值来访问这个列表项了(而且任你在代码中怎么找,也找不到声明或者初始化这个变量的地方)——当然前提是起的名字必须是唯一的。有意思吧?
第二种方式比较传统也比较少用,可以通过DOM对象访问每个元素。
废话不多说,来看看在代码中给列表插入列表项怎么做。
列表项对应着Gadget
API提供的一个名为item的对象实例,但我们要用new item()这样的语法来得到一个新的列表项并逐一设置它的属性么?不不,有更简便也更好玩的方法,我们只要新建一个字符串:
var itemXml= '<item name="album_item"><label>列表项</label></item>';
然后调用列表contentListBox的方法来添加就可以,像这样:
var newItem = contentListBox.appendElement(itemXml);
方便么?这种用法使得开发人员不需要为一个图形界面的组件掌握两套语法(XML的和JavaScript的),非常贴心。
好,现在来说另一个问题,既然不能为一个img对象的src属性指定一个网络地址,那到底如何显示网络上的图片呢?答案很长,如果你有了图片的url(就是 http://开头的那种啦),首先要通过XmlHttpRequest把图片的数据取回来,然后把这部分数据赋给src属性。
具体点,记得一个请求最重要的四部分数据么?url:就是该图片的url;请求类型:因为是要求数据,自然是“GET”;请求头:对本请求来说没有;消息体:同样没有。
所以发请求的部分并不困难,待请求的状态变为4,也就是说明回传数据已到达的时候,就可以从请求的responseStream这个属性得到图片的二进制数据。假设在代码中我们要显示的图片是<img name=”myImg”/>,记得么,使用名字可以直接访问这个图片,再假设我们的请求对象取名为xhRequest,像下面这样:
myImg.src=xhRequest. responseStream;
如此就可以了!哈哈,简单吧(我当初倒是找了半天,读过了YouTube Gadget的代码才参透呢,愚笨愚笨)。
在我们剩下的唯一一个重要函数Main的fetchAlbumThumbnail()中,就是使用这种方法来取得相册缩略图的图片并显示在Gadget的界面中的。
这个函数我就不逐一分解了,相信你一定看得懂。
大的方向上说,从Picasa服务器上取数据,有两种方式,一种是使用Google已经开放的各种语言的API,可以在页面http://code.google.com/apis/picasaweb/developers_guide_protocol.html找到很多相关的信息。另一种方式便是使用最朴素的网络请求方式来自己构造请求并解析回传的数据。
由于Picasa只提供了Java,.NET,Python和PHP的接口,而Gadget目前只能使用JavaScript,因此我们只能使用朴素方式。
继续第三节的路子,仍然使用XmlHttpRequest向Picasa服务发起请求,也要处理好四部分信息。
请求发向哪个URL:为了获取Picasa的相册信息,要向http://picasaweb.google.com/data/feed/api/user/default发请求,这个URL其实可以有很多变化的地方。例如user/default这个地方是请求所附token所属的用户相册信息,这里当然可以明确的指定用户名。”api”可以换成”base”,这个将影响回传数据的格式,但Goolge推荐使用api而不是base。
请求的类型:我们是要索取数据,因此这是一个查询的动作,应该使用GET。
请求头:只需要把token放进去就好。这样来放:
xhRequest.setRequestHeader('Authorization','GoogleLogin auth=' + token);
消息体:对于我们查询相册的请求,不需要任何的消息体。
具体的代码都在Main.prototype.fetchAlbumsInfo()函数中,就像这样:
Main.prototype.fetchAlbumsInfo=function() {
var url="http://picasaweb.google.com/data/feed/api/user/default";
var token=options.getValue("token");
xhRequest= createXhr();
xhRequest.open("GET", url, true);
xhRequest.setRequestHeader('Authorization','GoogleLogin auth=' + token);
xhRequest.send(null);
xhRequest.onreadystatechange =function(){
if (!xhRequest) {
return;
}
if (xhRequest.readyState != 4) {
return;
}
main.albums=parseAlbumFeed(xhRequest.responseText);
main.fetchAlbumThumbnail();
}
};
最后两个函数是下一步要做的工作:解析回传的相册数据,并下载每个相册的缩略图。
要想解析回传数据,首先得知道回传的数据是什么。你可以把这些数据打印出来看看,应该是类似下面的样子:
怎么,看着有点眼熟?没错,这个回传数据所使用的格式正是标准的Atom Feed(更多的描述可以参考W3C的标准和下面的链接:http://code.google.com/intl/zh-CN/apis/picasaweb/developers_guide_protocol.html)。
可以根据Atom Feed的格式来编写我们解析回传数据的函数parseAlbumFeed(),这个函数的作用是从回传的xml数据中找出我们关心的几样东西:该用户目前拥有的所有的相册信息,包括每个相册的标题,描述,访问权限以及缩略图的地址。找出这些信息以后,将会拼成一个包含相册(Album)的数组作为函数返回值。
具体代码如下:
function parseAlbumFeed(response) {
var doc = createDomDocument();
doc.loadXML(response);
//用户已经建立过的相册集合,函数的返回值
var albums = [];
var entryElements = doc.getElementsByTagName('entry');
//具体处理每个Album的信息
for (var i = 0; i < entryElements.length; i++) {
var entry = entryElements[i];
var album=new Album();
//相册标题
album.title=entry.getElementsByTagName('title')[0].text;
//相册描述
album.summary=entry.getElementsByTagName('summary')[0].text;
//相册的访问权限
album.access=entry.getElementsByTagName('gphoto:access')[0].text;
//相册的缩略图
var thumbnail=entry.getElementsByTagName('media:thumbnail')[0];
album.thumbnail=new Thumbnail(thumbnail.getAttribute('url'));
albums.push(album);
}
return albums;
};
这个函数中用到了一些我们还没有新建的类,相册(Album)以及缩略图(Thumbnail)。这些类的声明可以放在一个新的名为album.js的文件中,并在我们整个Gadget的main.xml文件中指名要导入它。因此main.xml的最后几行应该看上去是这个样子:
<script src="album.js" />
<script src="main.js" />
</view>
而album.js的内容大体如下:
function Album() {
this.title = "";
this.summary="";
this.access="";
this.thumbnail=#ff0000;
}
function Thumbnail(url) {
this.url = url;
this.width = 40;
this.height = 40;
this.src = undefined; // XML response stream
}
最后还要在main.js里面添加一个函数createDomDocument(),用来提供一个DOM对象供我们解析XML用。代码如下:
function createDomDocument() {
var doc = new DOMDocument();
try {
doc.resolveExternals = false;
doc.validateOnParse = false;
doc.setProperty('ProhibitDTD', false);
} catch(e) {
debug.warning('Could not set MS specific properties.');
}
return doc;
}
下一节来说说怎么取得相册的缩略图并显示在Gadget的界面中。
向Google的服务器发起登录请求之后,得到了免死金牌token,以后就可以拿着这个token去犯罪,不是,去Google的其它服务取数据,但是在此之前应该第一,从响应的消息中把token找出来;第二,这个token应该想办法保存起来,以备以后使用。
上一节已经把响应的内容打印了出来,它的格式也很简单,因此用下面的代码很容易就可以把响应的内容转成方便我们使用的形式,即一个map的形式,通过键值对来存储:
function parseResponse(response) {
var responseLines = response.split('\n');
var responseData = {};
for (var i = 0; i < responseLines.length; ++i) {
var split = responseLines[i].indexOf('=');
var key = responseLines[i].substr(0, split);
var value = responseLines[i].substr(split + 1);
responseData[key] = value;
}
return responseData;
};
在我们的相应回调函数里,就可以调用这个函数处理一下响应,从结果中取键为”Auth”这一项的值,并保存在Gadget
Host为我们准备好的一个负责持久化的对象options中。找到上一节Main.prototype.login的代码,把响应的回调函数改成下面的样子:
xhRequest.onreadystatechange =function(){
if (!xhRequest) {
return;
}
if (xhRequest.readyState != 4) {
return;
}
//调用新写的函数来解析响应内容
var responseData = parseResponse(xhRequest.responseText);
var token = responseData['Auth'];
//这里来记住已经登录过的用户名和密码
options.putValue("username","mymail2009.test@gmail.com");
options.putValue("password","mymail2009");
options.putValue("token", token);
options.encryptValue("token");
main.onLoginSuccess();
}
最后加的一行main.onLoginSuccess()就是我们下一步动作的起点,在这里应该开始去取用户mymail2009.test@gmail.com所拥有的相册信息了,我们先声明一个空函数放在那里。
Main.prototype.onLoginSuccess=function(){
this.fetchAlbumsInfo();
};
//取相册信息的函数
Main.prototype.fetchAlbumsInfo=function() {
};
继续之前多扯两句options这个对象,这是Gadget Host提供的持久化对象,你可以从代码中看到它还有对存储的内容进行加密的功能,Google的文档中提到这个options对象在后台实际上是把内容保存在一个XML文件中,当然该文件的位置是不会告诉你的啦,哈哈。
下一节将向Picasa服务发起请求!
Google帐户最早用来申请巨大的Gmail邮箱(如今看来,一般个大吧),随着后来的Blogger,Picasa,Docs等各种服务上线,也就顺路继承了过来。现在使用一个Google帐户,就可以同时使用这些服务。
既然我们打算写一个从Picasa取相册数据的Gadget,就免不了要先了解一些和Goolge帐户有关的知识。因为Picasa的数据也是受保护的,并非谁要看都可以(公开的相册除外哦,那都是炫耀册,巴不得全天下人都看见呢),我们的程序也不例外,要想取到相册的数据,程序必须向Google的服务器证明自己得到了相应用户的授权。
一个人类用户当然可以这样做:打开Picasa的首页,发现要求登录,于是输入自己的用户名密码,成功后就查看自己的相册。我们的程序可干不了,它不会打开浏览器,好吧,这个它会,但打开以后它找不着用户名的输入框在哪,即便找到了,也不知该往里面填什么,即便填对了,也不知要看什么,即便看到了,也看不懂,即便看懂了也学不会……(读者:你贫不贫?)
所以一切的一切都还要咱们自己来写,当然少不了Google的帮忙。
为了方便应用程序的登录,Google在自己的服务器上开放了被称之为“Google Account Authentication”的服务,我们只用到其中一种方式:ClientLogin。使用这种方式访问Google的服务大致是下面的流程:

很容易看出来,这基本上是一个两步骤的工作:首先使用一个Google帐户访问Google
Account Authentication 服务,并得到一个可以合法访问服务数据的token(Google把它叫做得到一个“授权”,不过习惯上还是叫token吧,就是令牌,拿了以后皇帝不能砍你头的那种,此过程也叫做申请一个token);使用上一步得到的token去访问具体的服务并取得数据(我们的例子中就是访问Picasa服务)。
有一些东西从图上看不出,我来说一说。一是程序访问Gmail的时候使用的不是这种方式(毕竟Gmail太早啦,那时连Google自己都没有考虑清楚吧),但其他大部分Goolge服务,包括Calendar,Docs,Picasa,Blogger,Contacts,Google
Apps等等,都是上面这个流程。二是并非申请了一个token以后,就可以访问Google所有的服务,实际上需要为每个服务申请不同的token。
具体到代码中,我们使用XmlHttpRequest对象来发送请求并且接受回传的数据。
XmlHttpRequest是Gadget Host提供的一个类型(注意我没有说对象,因此要用的时候你还得自己初始化,也就是new一下,哈哈),其行为与W3C所指定的标准XmlHttpRequest相同。再一次的,不要联想到浏览器,你不能假设这个XmlHttpRequest与IE或者FireFox提供的XmlHttpRequest有任何联系,更不能依赖这样的假设来编写程序。
好,废话少说,还用上一节新建的“白Gadget“(笑),在main.js文件里添加这样一个函数:
function createXhr() {
var xhr;
try {
xhr = framework.google.betaXmlHttpRequest2();
} catch (e) {
xhr = new XMLHttpRequest();
}
return xhr;
}
调用这个函数就可以得到一个XmlHttpRequest的对象啦。
然后为我们的Gadget添加一个主类,并把需要的对象引用也声明好,这些都写在main.js文件中,像这样:
var xhRequest=null;
var main=new Main();
//Gadget启动时便登录
function view_onOpen() {
main.login();
}
function Main(){
this.albums=[];
}
//具体的登录函数
Main.prototype.login=function(){
}
我们就要在Main.login()函数中写我们取token的逻辑。
详细说说申请token的过程。请求是通过XmlHttpRequest对象发起的,而对一个请求来说,最重要的信息有四个:请求的URL,请求的类型,请求头和消息体。
URL是说你的请求要发往哪里,既然我们要使用Google的服务,那当然要往Google那里发了,具体应该为:
https://www.google.com/accounts/ClientLogin
如果你没有看出这是一个安全的https请求,那我提醒一下(如果你看出来了,我就不提醒了,笑)。
请求的类型是指你要Google的服务器替你做什么事情,是返回你要查询的数据?还是为你更新已有的数据,抑或仅仅是提交一些数据,还是要服务器帮你删除一些数据?
Google的服务器通过你提交请求的类型来做相应的操作,每一种操作的类型对应如下:
- 查询 GET
- 提交 POST
- 更新 PUT
- 删除 DELETE
看着眼熟么?没错,正是轻量级的Web Service接口REST!
我们做登录显然是一个提交的动作,
要把我们的用户名和密码告诉Google,因此我们的请求类型是POST。
对登录来说,请求头没有特殊要求,只需要请求头Content-Type,其值为application/x-www-form-urlencoded
所需的用户名,密码等信息被统一称为“属性”,属性的值将放在消息体中发送。因此你的消息体看起来是下面这个样子的一个字符串:
Email=mymail2009.test%40gmail.com&Passwd=mymail2009&service=lh2&source=gd-picasa-gadget-1.0.0.0&accountType=HOSTED_OR_GOOGLE
注意其中红色的部分,用户名和密码的位置你当然很容易找到,”service=lh2”这一项就指明了你要为访问什么服务申请token,lh2是指Picasa,如果访问Google Docs则要填writely,详细的列表可以看这一节最后的附录。
好,把登录的代码整个贴出来,你应该很容易找到以上四部分对应的地方。
Main.prototype.login=function(){
xhRequest= createXhr();
//请求的URL
var url="https://www.google.com/accounts/ClientLogin";
//消息体
var data="Email=mymail2009.test%40gmail.com&Passwd=mymail2009&service=lh2&source=gd-picasa-gadget-1.0.0.2&accountType=HOSTED_OR_GOOGLE";
xhRequest.onreadystatechange =function(){
if (!xhRequest) {
return;
}
if (xhRequest.readyState != 4) {
return;
}
//如果下面这行能够被执行,说明登录请求已经有数据返回
alert(“登录动作完毕啦!”);
alert(xhRequest.responseText);
}//接受数据后的回调函数
//请求的类型,是POST
xhRequest.open('POST', url, true);
//请求头
xhRequest.setRequestHeader("Content-Type","application/x-www-form-urlencoded");
xhRequest.send(data);
};
在请求的回调函数中,目前只是先简单的打印了相应的文本内容,实际上应该在这里做更多的事,详情咱们下节再聊。如果你看到类似下面这样的输出内容,说明登录的请求成功了。如果没有成功,很可能是因为我已经换掉了用户名和密码,用你自己的Google帐户试试看。
应该看到的内容:
SID=
DQAAAHYAAADYQ4hToTAEYRu0uEXP9yXZ1uc_W3-kBtZFpug78XQDGiykOb-Sv2qdXtdUOL-
npRJm9SSq-AEvSBodrcuy3UwgFM8SX_z6fXzpGaJzHzQx5YTzR0AJHCEkFh
4yOoBFs0iCE2LI0LWQs6_2BFyIuLLMwRA8m3vfuVzNE3CHjrUHZA
LSID=
DQAAAHgAAAClSiMWRfKAonW8zIytZ7NEizJNMQZojiNqsDxm3elei36MV
7GzM72bMiqdQawt8Fd1Dpp68p5bs1XYOXUPmDunUsZM1BZsAiXbIEouAJz1XjlysUQG-0p9969zYCvUm2tqWkA1BFVU2UqvjMAaBSgj10VkZzvcAbZB8nQf_mwRyg
Auth=
DQAAAHcAAAClSiMWRfKAonW8zIytZ7NEizJNMQZojiNqsDxm3elei36
MV7GzM72bMiqdQawt8FcmxySIt75kfLxcis5BZnNCsyVuCwKM-DtNZcToUtm9IWoJyvNbUD9UTFYZPdBu1OyXsfY_QJHZfZdAT2QC
cExSIYKMvLfhhit9RPz4Gk2xlQ/n
Auth那一项后面的值就是token啦,可以不被砍头了。
附录:已知的Google服务及服务名
|
Calendar
Data API
|
cl
|
|
Google
Base Data API
|
gbase
|
|
Blogger
Data API
|
blogger
|
|
Contacts
Data API
|
cp
|
|
Documents
List Data API
|
writely
|
|
Picasa
Web Albums Data API
|
lh2
|
|
Google
Apps Provisioning API
|
apps
|
|
Spreadsheets
Data API
|
wise
|
|
YouTube
Data API
|
youtube
|
前文说道开发一个Gadget可以分为两个步骤:先写界面的XML文件,再写逻辑部分的JavaScript。我们就遵循这个步骤来写一个再简单也不过的Gadget。
用到的工具有两个,一个是随Google Desktop SDK附带的Gadget Designer,用来编写并有限的预览界面,还可以调试JavaScript(这个就更有限了);一个是Google Desktop,用来测试写好的Gadget。下面要写的例子是我在为某研究院某个项目策划阶段作POC时所写的一个小例子,可以显示一个Google用户的Picasa相册中的Album名称和缩略图。虽然很小,但包含了Google账户的自动登录,显示网络图片,XmlHttpRequest的使用等很多实用技巧。整个完成之后是这个样子:

请跟我一起来。现在打开Gadget Designer,选择File->New Gadget,输入了名称“Picasa”之后,就可以看到一个完整Gadget的雏形了。你可以找到这个项目所在的文件夹,双击其中的gadget.gmanifest,此时如果你已经安装了Google Desktop,就可以看到Desktop自动启动,并把这个很“白”的Gadget(别笑,除了一张白色背景图片以外,确实什么也没有)显示在Sidebar中。如图:
到项目文件夹里可以看到一个main.xml文件和一个main.js文件。我们的界面就是在main.xml文件里指定的,打开它,可以看见它指定了一张GadgetDesigner帮我们生成的白色png图片作背景,还指定了我们要导入哪些个.js文件。我们来小改两个地方:
<view height="150" width="250" onopen="view_onOpen()">
<img src="stock_images\background.png" />
<script src="main.js" />
</view>
一是把view的height改成250,二是给img元素添加一个属性name并给一个值,就像这样:
<img name=”bgImage” src="stock_images\background.png" />
然后双击gadget.gmanifest,看看更改效果:

乍一看貌似没什么改变,但是注意看我用黑色线圈出来的那一条横杠,那是我们的Gadget的下边沿,说明它的高度还是变化了,但是白色的背景没有变,因为我们没有改变背景图片的大小。现在通过.js文件中代码的方式来改变背景图片的高度,可以看出些有意思的东西。
打开main.js文件,你应该会看到一个view_onOpen()函数,这就是Gadget启动时会自动调用的第一个函数(好吧,并不严格,但是在调用的顺序上,它的确是相当靠前的),我们就在这个函数内部添加下面这一句:
bgImage.height=250;
再双击gadget.gmanifest运行看看,白色背景也变高了吧。
我知道你一定会问,代码里的bgImage是什么东西?怎么没见在任何地方声明这个变量,也没见任何地方作初始化呢?回想我们刚才在main.xml文件里做了什么?我们给背景图片取了一个名字,叫bgImage,而且别怀疑,你在代码里访问的这个bgImage,正是那张图片!背后的工作就是Gadget Host通过JavaScript引擎为我们做的,凡是在.xml文件里放置的东西(无论什么,图片也好,按钮也好,一个抽象的div也好),只要你给了一个name属性,在JavaScript代码中就可以直接使用这个名字来访问该对象(前提是你给的名字得是独一无二的),这与浏览器中随时可以访问document对象而不用做任何声明一样,那是浏览器这个运行环境提供的对象,随时可用。
另一个值得注意的地方是在.xml文件里,属性的值都必须加上引号,像height=”250”(因为那里使用的是标准的xml语法),而在JavaScript代码中,就要根据属性具体的类型来决定,像高度这种整数型的值,就不用加。
你可能还会问,那么bgImage这个对象,是什么类型的,它有些什么属性和方法可供我使用呢?它是一个img类型的对象,参考http://code.google.com/intl/zh-CN/apis/desktop/docs/gadget_apiref.html这个链接,这也是Google Desktop Gadget的API参考页面,列出了Gadget Host提供的各种对象属性和方法的说明(虽然事实验证,Google自己列的这些都不全面,后话)。
最后叮嘱一句:尽管main.xml文件里的东西(什么img啊,以后还会加进div啊,checkbox之类的东西)看起来多么的像HTML,Gadget都和Web没有天然的联系。Google自己发布了一些Gadget,例如Gmail和Google Docs,外观与这两个服务的网页非常像,再加上Gadget也主要使用JavaScript开发(也少不了Universal Gadget跟着掺合),间接导致了总有人把Gadget显示的地方考虑成一个小的浏览器窗口,而想把Web的一些东西简单的放在这里,到底行不行呢?李宁说:一切皆有可能。阿迪说:没有不可能。匹克说:我能,无限可能。我要说:可能,但很难(笑)。
所以在编写Gadget的时候,最好的方法是把它当成纯粹的桌面程序,忘掉Web的那一套。
这一节给大家入个门,下一节开始说说在Gadget中怎么做Google帐户的登录,还会很罗嗦的,请见谅(笑)。
在Gadget开发人员看来——我当然是指你我这样的IT民工,来开发一个Gadget的人,而不是Google大楼里成天琢磨怎么和微软对着干的那帮子人——一个Gadget由三大部分组成:描述UI的一系列.xml文件;存放程序逻辑的.js文件以及资源。
下面是一个Gadget项目在Google Desktop Disigner里面的结构截图。
资源这东西好理解,无非是程序要用到的各种图片啦,字符串啦等等。读者:字符串?什么意思?答:把程序会用到的一系列字符串统一存放,想引用的时候使用一个常量名字就可以,而不必在需要这些字符串的地方每次都重写一遍,和Java中的property文件作用类似。
其余的两部分会分节来详细讲解。
当然说只有三部分,是指我们大多只关心这么多,实际上还有第四部分,一个Gadget Settings文件,其中大多是关于这个Gadget的元信息,什么作者啊,创建日期啊,uuid啊,户口所在地啊,最高学历啊,婚姻状况啊,哦,我给说成简历了(笑)。
前面也说到过,一个Gadget其实就是一个桌面应用程序(再一次的,不管写起来某些语法多么得像HTML,Gadget与Web都没有天然的联系),只不过这个程序在Gadget Host的管理之下,行话叫“托管”。Windows下没有单独的Gadget Host,它被合并在Google Desktop里面(算是另一种捆绑吧)。而Linux下的确有干干净净的Gadget Host,且有源码下载,我们所有对Gadget的理解也都源于这个版本和相关的文档。
那么在Gadget Host看来,一个Gadget是什么东西呢?
以我写的一个小Picasa Gadget为例,在Picasa Gadget初次加载之前,它是一个.gg的压缩包(其实就是一个标准的zip包,被改了后缀名而已),Gadget Host会从中读取需要的文件,然后做相应的解释。
Gadget Host可以看成只有两部分组成:一个UI的渲染器和一个JavaScript引擎。
说UI渲染器之前就不得不回头重提刚才说到的一个Gadget包括了一系列.xml文件这件事。实际上这些.xml文件就是用来指定你想写的Gadget的界面的,就是说,你的Gadget跑起来以后长成什么样子,是由这些个.xml文件来决定的(当然,严格说来可以使用JavaScript在运行时改变一些内容,但请不要抬杠,笑)。
这些.xml文件中最主要的是main.xml这个文件,你的Gadget窗口有多大,在什么位置有几个按钮,列表有没有滚动条,背景是什么颜色等等,都在这里指定。还包括这些东西上的事件监听函数也一并在这里声明(不知为何,让我莫名的想起微软的MFC,当然,严格说来可以使用JavaScript在运行时动态改变这些内容,但请不要再次抬杠,笑)。
UI渲染器干什么呢?就是来把这个.xml所要求的界面转换成具体的系统调用,让操作系统来完成绘图(好吧好吧,你喜欢严格,那我告诉你,Linux版本下首先被转换为Qt的C++类,由Qt来发起对系统绘图的调用)。
既然Gadget的程序逻辑都使用JavaScript来编写,理所应当的,Gadget Host必然要包含一个JavaScript解释器来解释这些代码,这个解释器也被叫做JavaScript引擎。Gadget Host里确实有这么个东西,叫做Spider Monkey,它恰好也是FireFox所使用的JavaScript引擎。广义上说,一个引擎的作用主要是解释它遇到的一切JavaScript代码,如果代码使用到核心JavaScript的功能和对象,它便直接提供;如果代码使用到了一些依赖于底层的对象(例如Gadget Host就提供了很多专有的JavaScript对象和方法供使用,这些都是核心JavaScript之外的东西),则引擎还要负责转发这样的请求(你可以说,这实际上是适配器做的事,我这样简化有助于理解,请不要一再抬杠,笑)。
也可以这样从逻辑上看Gadget的组成:即一个Gadget就是一组图形界面,加这些界面上每个控件(按钮啊,列表啊,输入框等等)的事件监听函数,这种界面描述与事件逻辑分离的程序模型,和微软的XAML+C#简直如出一辙。因此一个Gadget的开发实际上也就可以分为这两大步骤:先写界面的XML文件,再写逻辑部分的JavaScript。下面一节就用一个小例子来看看具体如何做。别嫌我说得太详细哦。
去年这一年被研究生院和所里揪着干了不少自己并不擅长的事,其中就包括为各种大小活动设计PPT,邀请函,节目表之类的东西。年底了,拿出来看看也能理一理自己从无到有,从门外汉到菜鸟的成长过程。共赏,共析哈。 
最早的一张,元旦晚会时为模特队做的。本来他们自己做了一套共计3张的PPT,赶巧我这张已经做好了,便让他们自己选,结果还是选了我的,呵呵。 
同一场晚会为舞蹈队做的,没太多东西,只是字体和配色斟酌了一阵子。 
青年博客大赛决赛颁奖晚会的主题PPT,刚提交第一版便遭到老师表扬,结果一点修改都没有做便获通过。 
同一场晚会的领导致辞图,风格还挺一致的吧?(笑) 
仍然是博客大赛决赛颁奖晚会,那一次晚会因为外请节目比较多,整体水平着实不低呢。 
计算所青年歌手大赛的节目单,其实参考了很有名气的设计,所以才能做成这个样子,不敢专美,特此声明。 
计算所青歌赛的主题PPT,多亏有设计的四大原则帮忙啊。后来一个计算所的师兄还问我把这张片子讨了去,说是只看一眼就喜欢上了里面的女孩,还一个劲的问我她是谁,是咱所的么,我赶紧解释说不是不是…… 
最近一次为街舞社的表演做的PPT,发现自己的风格算是定型了,怎么看都似曾相识,当然也可以说,是黔驴技穷了……
按:系列文章,将谈及Google Gadget的体系结构和开发入门,后期还会有和类似技术Mozilla Prism的对比。
开始之前先澄清一件事,这里所说的Gadget实际上是指Google
Desktop Gadget,而不是指在iGoogle或者FaceBook上运行的Gadget,那个叫做Universal
Gadget。
细说起来,其实Gadget和Universal
Gadget不仅名称不同,在实现上也完全是两回事。从使用者的角度看,Univeral Gadget就是一个HTML的页面,只不过在显示的时候是实时从iGoogle之类的容器网站上下载过来并展现在一个iframe里面的。而Desktop Gadget则是一个不折不扣的桌面应用程序(虽然运行在Google Desktop这个容器中)。
从开发人员的角度看,Universal Gadget是一个JavaScript文件和XML文件的集合,由容器网站(例如iGoogle,Facebook等等)来渲染成HTML页面并呈现给最终用户。在一个Universal Gadget中使用的技术都是标准的Web技术,其能量也限制在浏览器的框架中。
而在开发一个Desktop Gadget时,虽然也使用XML文件来指定程序的UI,使用JavaScript来实现程序的逻辑,但与Web或者浏览器都没有天然的联系,说是完全的另一套程序开发体系也不为过(使用的XML语法与Universal Gadget不同,能够使用的JavaScript的对象及功能也不同)。
但另一方面的情况导致两者时常被人混为一谈,那就是,一个Universal Gadget是可以被加载到Desktop
Gadget的面板中并正常运行的(严格的说只有一部分),而一部分Desktop Gadget也可以加载到iGoogle网站中运行(因而使它看上去像一个Universal Gadget,当然需要系统已安装了Google Desktop才可以)。
书归正传,下面就来说Gadget到底是什么,以及它的体系结构和背后思想。
(注:以下如果没有特别指明,提起Gadget全都是指Desktop
Gadget,而iGoogle上的Gadget会指明为Universal Gadget)
Java号称对Unicode提供天然的支持,这话在很久很久以前就已经是假的了(不过曾经是真的),实际上,到JDK5.0为止,Java才算刚刚跟上Unicode的脚步,开始提供对 增补字符的支持。
现在的Unicode码空间为U+0000到U+10FFFF,一共1114112个码位,其中只有1,112,064 个码位是合法的(我来替你做算术,有2048个码位不合法),但并不是说现在的Unicode就有这么多个字符了,实际上其中很多码位还是空闲的,到Unicode 4.0 规范为止,只有96,382个码位被分配了字符(但无论如何,仍比很多人认为的65536个字符要多得多了)。其中U+0000 到U+FFFF的部分被称为 基本多语言面(Basic Multilingual Plane,BMP)。U+10000及以上的字符称为补充字符。在Java中(Java1.5之后),补充字符使用两个char型变量来表示,这两个char型变量就组成了所谓的surrogate pair(在底层实际上是使用一个int进行表示的)。第一个char型变量的范围称为“高代理部分”(high-surrogates range,从"uD800到"uDBFF,共1024个码位), 第二个char型变量的范围称为low-surrogates range(从"uDC00到"uDFFF,共1024个码位),这样使用surrogate pair可以表示的字符数一共是1024的平方计1048576个,加上BMP的65536个码位,去掉2048个非法的码位,正好是1,112,064个码位。
关于Unicode的码空间实际上有一些稍不小心就会让人犯错的地方。比如我们都知道从U+0000到U+FFFF的部分被称为基本多语言面(Basic Multilingual Plane,BMP),这个范围内的字符在使用UTF-16编码时,只需要一个char型变量就可以保存。仔细看看这个范围,应该有65536这么大,因此你会说单字节的UTF-16编码能够表示65536个字符,你也会说Unicode的基本多语言面包含65536个字符,但是再想想刚才说过的surrogate pair,一个UTF-16表示的增补字符(再一次的,需要两个char型变量才能表示的字符)怎样才能被正确的识别为增补字符,而不是两个普通的字符呢?答案你也知道,就是通过看它的第一个char是不是在高代理范围内,第二个char是不是在低代理范围内来决定,这也意味着,高代理和低代理所占的共2048个码位(从0xD800到0xDFFF)是不能分配给其他字符的。
但这是对UTF-16这种编码方法而言,而对Unicode这样的字符集呢?在Unicode的编号中,U+D800到U+DFFF是否有字符分配?答案是也没有!这是典型的字符集为方便编码方法而做的安排(你问他们这么做的目的?当然是希望基本多语言面中的字符和一个char型的UTF-16编码的字符能够一一对应,少些麻烦,从中我们也能看出UTF-16与Unicode间很深的渊源与结合)。也就是说,无论Unicode还是UTF-16编码后的字符,在0x0000至0xFFFF这个范围内,只有63488个字符。这就好比最初的CPU被勉强拿来做多媒体应用,用得多了,CPU就不得不修正自己从硬件上对多媒体应用提供支持了。
尽管不情愿,但说到这里总还得扯扯相关的概念:代码点和代码单元。
代码点(Code Point)就是指Unicode中为字符分配的编号,一个字符只占一个代码点,例如我们说到字符“汉”,它的代码点是U+6C49。
代码单元(Code Unit)则是针对编码方法而言,它指的是编码方法中对一个字符编码以后所占的最小存储单元。例如UTF-8中,代码单元是一个字节,因为一个字符可以被编码为1个,2个或者3个4个字节;在UTF-16中,代码单元变成了两个字节(就是一个char),因为一个字符可以被编码为1个或2个char(你找不到比一个char还小的UTF-16编码的字符,嘿嘿)。说得再罗嗦一点,一个字符,仅仅对应一个代码点,但却可能有多个代码单元(即可能被编码为2个char)。
以上概念绝非学术化的绕口令,这意味着当你想以一种统一的方式指定自己使用什么字符的时候,使用代码点(即你告诉你的程序,你要用Unicode中的第几个字符)总是比使用代码单元更好(因为这样做的话你还得区分情况,有时候提供一个16进制数字,有时候要提供两个)。
例如我们有一个增补字符???(哈哈,你看到了三个问号对吧?因为我的系统显示不出这个字符),它在Unicode中的编号是U+2F81A,当在程序中需要使用这个字符的时候,就可以这样来写:
String s=String.valueOf(Character.toChars(0x2F81A));
char[]chars=s.toCharArray();
for(char c:chars){
System.out.format("%x",(short)c);
}
后面的for循环把这个字符的UTF-16编码打印了出来,结果是
d87edc1a
注意到了吗?这个字符变成了两个char型变量,其中0xd87e就是高代理部分的值,0xdc1a就是低代理的值。
如果你是JVM的设计者,让你来决定JVM中所有字符的表示形式,你会不会允许使用各种编码方式的字符并存?
我想你的答案是不会,如果在内存中的Java字符可以以GB2312,UTF-16,BIG5等各种编码形式存在,那么对开发者来说,连进行最基本的字符串打印、连接等操作都会寸步难行。例如一个GB2312的字符串后面连接一个UTF-8的字符串,那么连接后的最终结果应该是什么编码的呢?你选哪一个都没有道理。
因此牢记下面这句话,这也是Java开发者的共同意志:在Java中,字符只以一种编码形式存在,那就是UTF-16。
但“在Java中”到底是指在哪里呢?就是指在JVM中,在内存中,在你的代码里声明的每一个char,String类型的变量中。例如你在程序中这样写
char han='汉';
在内存的相应区域,这个字符就表示为0x6C49。可以用下面的代码证明一下:
char han='汉';
System.out.format("%x",(short)han);
输出是:
6c49
反过来用UTF-16编码来指定一个字符也可以,像这样:
char han=0x6c49;
System.out.println(han);
输出是:
汉
这其实也是说,只要你正确的读入了“汉”这个字,那么它在内存中的表示形式一定是0x6C49,没有任何其他的值能代表这个字(当然,如果你读错了,那结果是什么就不知道了,范伟说:读,读错了呀,那还等于好几亿呢;本山大哥说:好几亿你也没答上,请听下一题)。
JVM的这种约定使得一个字符存在的世界分为了两部分:JVM内部和OS的文件系统。在JVM内部,统一使用UTF-16表示,当这个字符被从JVM内部移到外部(即保存为文件系统中的一个文件的内容时),就进行了编码转换,使用了具体的编码方案(也有一种很特殊的情况,使得在JVM内部也需要转换,不过这个是后话)。
因此可以说,所有的编码转换就只发生在边界的地方,JVM和OS的交界处,也就是你的各种输入输出流(或者Reader,Writer类)起作用的地方。
话头扯到这里就必须接着说Java的IO系统。
尽管看上去混乱繁杂,但是所有的IO基本上可以分为两大阵营:面向字符的Reader啊Wrtier啊,以及面向字节的输入输出流。
下面我来逐一分解,其实一点也不难。
面向字符和面向字节中的所谓“面向”什么,是指这些类在处理输入输出的时候,在哪个意义上保持一致。如果面向字节,那么这类工作要保证系统中的文件二进制内容和读入JVM内部的二进制内容要一致。不能变换任何0和1的顺序。因此这是一种非常“忠实于原著”的做法(偶然间让我想起郭敬明抄袭庄羽的文章,那家伙,太忠实于原著了,笑)。
这种输入输出方式很适合读入视频文件或者音频文件,或者任何不需要做变换的文件内容。
而面向字符的IO是指希望系统中的文件的字符和读入内存的“字符”(注意和字节的区别)要一致。例如我们的中文版WindowsXP系统上有一个GBK的文本文件,其中有一个“汉”字,这个字的GBK编码是0xBABA(而UTF-16编码是0x6C49),当我们使用面向字符的IO把它读入内存并保存在一个char型变量中时,我希望IO系统不要傻傻的直接把0xBABA放到这个char型变量中,我甚至都不关心这个char型变量具体的二进制内容到底是多少,我只希望这个字符读进来之后仍然是“汉”这个字。
从这个意义上也可以看出,面向字符的IO类,也就是Reader和Writer类,实际上隐式的为我们做了编码转换,在输出时,将内存中的UTF-16编码字符使用系统默认的编码方式进行了编码,而在输入时,将文件系统中已经编码过的字符使用默认编码方案进行了还原。我两次提到“默认”,是说Reader和Writer的聪明也仅此而已了,它们只会使用这个默认的编码来做转换,你不能为一个Reader或者Writer指定转换时使用的编码。这也意味着,如果你使用中文版WindowsXP系统,而上面存放了一个UTF-8编码的文件,当你使用Reader类来读入的时候,它会傻傻的使用GBK来做转换,转换后的内容当然驴唇不对马嘴!
这种笨,有时候其实是一种傻瓜式的功能提供方式,对大多数初级用户(以及不需要跨平台的高级用户)来说反而是件好事。
但我们不一样啦,我们都是国家栋梁,肩负着赶英超美的责任,必须师夷长技以治夷,所以我们总还要和GBK编码以外的文件打交道。
说了上面这些内容,想必聪明的读者已经看出来,所谓编码转换就是一个字符与字节之间的转换,因此Java的IO系统中能够指定转换编码的地方,也就在字符与字节转换的地方,那就是(读者:InputSteamReader和OutputStreamWriter!作者:太强了,都会抢答了!)
这两个类是字节流和字符流之间的适配器类,因此他们肩负着编码转换的任务简直太自然啦!要注意,实际上也只能在这两类实例化的时候指定编码,是不是很好记呢?
下面来写一段小程序,来把“汉”字用我们非常崇拜的UTF-8编码写到文件中!
try{
PrintWriter out=new PrintWriter(new OutputStreamWriter(new FileOutputStream("c:/utf-8.txt"),"UTF-8"));
try{
out.write("汉");
}finally{
out.close();
}
}catch(IOException e){
throw new RuntimeException(e);
}
运行之后到c盘下去找utf-8.txt这个文件,用UltraEdit打开,使用16进制查看,看到了什么?它的值是0xE6B189!(这正是“汉”这个字的UTF-8编码)噢耶!(读者:这,这有什么好高兴的……)
下一节我们来看看实现这种操作的其他方式,读到这里,你已经基本上是字符编码的高手了哦。
接着上节的思路说,一个网页要想在浏览器中能够正确显示,需要在三个地方保持编码的一致:网页文件,网页编码声明和浏览器编码设置。
首先是网页文件本身的编码,即网页文件在被创建的时候使用什么编码来保存。这个完全取决于创建该网页的人员使用了什么编码保存,而进一步的取决于该人员使用的操作系统。例如我们使用的中文版WindowsXP系统,当你新建一个文本文件,写入一些内容,并按下ctrl+s进行保存的那一刻,操作系统就替你使用GBK编码将文件进行了保存(没有使用UTF-8,也没有使用UTF-16)。而使用了英文系统的人,系统会使用ISO-8859-1进行保存,这也意味着,在英文系统的文件中如果输入一个汉字,是无法进行保存的(当然,你甚至都无法输入)。
一个在创建XML文件时(创建HTML的时候倒很少有人这么做)常见的误解是以为只要在页面的encoding部分声明了UTF-8,则文件就会被保存为UTF-8格式。这实在是……怎么说呢,不能埋怨大家。实际上XML文件中encoding部分与HTML文件中的charset中一样,只是告诉“别人”(这个别人可能是浏览你的页面的人,可能是浏览器,也可能是处理你页面的程序,别人需要知道这个,因为除非你告诉他们,否则谁也猜不出你用了什么编码,仅通过文件的内容判断不出使用了什么编码,这是真的)这个文件使用了什么编码,唯独操作系统不会搭理,它仍然会按自己默认的编码方式保存文件(再一次的,在我们的中文WindowsXP系统中,使用GBK保存)。至于这个文件是不是真的是encoding或者charset所声明的那种编码保存的呢?答案是不一定!
例如新浪的页面就“声称”他是用GB2312编码保存的,但实际上却是GBK,也有无数的二把刀程序员用系统默认的GBK保存了他们的XML文件,却在他们的encoding中信誓旦旦的说是UTF-8的。
这就是我们所说的第二个位置,网页编码声明中的编码应该与网页文件保存时使用的编码一致。
而浏览器的编码设置实际上并不严格,就像我们第三节所说的那样,在浏览器中选择使用GB2312来查看,它实际上仍然会使用GBK进行。而且浏览器还有这样一种好习惯,即它会尽量猜测使用什么编码查看最合适。
我要重申的是,网页文件的编码和网页文件中声明的编码保持一致,这是一个极好的建议(值得遵循,会与人方便,与己方便),但如果不一致,只要网页文件的编码与浏览器的编码设置一致,也是可以正确显示的。
例如有这样一个页面,它使用GBK保存,但声明自己是UTF-8的。这个时候用浏览器打开它,首先会看到乱码,因为这个页面“告诉”浏览器用UTF-8显示,浏览器会很尊重这个提示,于是乱码一片。但当手工把浏览器设为GBK之后,显示正常。
说了以上四节这么多,后面我们就来侃侃Java里的字符编码,你会发现有意思且挠头的事情很多,但一旦弄通,天下无敌(不过不要像东方不败那样才好)。
GB2312是对中国的开发人员来说很重要的一个词汇,它的来龙去脉并不需要我在这里赘述,随便Google之便明白无误。我只是想提一句,记得前一节说到编码字符集和字符集编码不是一回事,而有的字符集编码又实际上没有做任何事,GB2312正是这样一种东西!
GB2312最初指的是一个编码字符集,其中包含了ASCII所包含的英文字符,同时加入了6763个简体汉字以及其他一些ASCII之外的符号。与Unicode有UTF-8和UTF-16一样(当然, UTF-8和UTF-16也没有被限定只能用来对Unicode进行编码,实际上,你用它对视频进行编码都是可以的,只是编出的文件没有播放器支持罢了,哈哈),GB2312也有自己的编码方案,但这个方案直接使用一个字符在GB2312中的编号作为存储值(与UTF-32的做法类似),也因此,这个编码方案甚至没有正式的名称。我们日常说起GB2312的时候,常常即指这个字符集,也指这种编码方案。
GBK是GB2312的后续标准,添加了更多的汉字和特殊符号,类似的是,GBK也是同时指他的字符集和他的编码。
GBK还是现如今中文Windows操作系统的系统默认编码(这正是几乎所有网页上的,文件里的乱码问题的根源)。
我们可以这样来验证,使用以下的Java代码:
String encoding=System.getProperty("file.encoding");
System.out.println(encoding);
输出结果为
GBK
(什么?你的输出不是这样?怎么可能?完了,我的牌子要砸了,等等,你用的繁体版XP?我说你这同志在这里捣什么乱?去!去!)
说到GB2312和GBK就不得不提中文网页的编码。尽管很多新开发的Web系统和新上线的注重国际化的网站都开始使用UTF-8,仍有相当一部分的中文媒体坚持使用GB2312和GBK,例如新浪的页面。其中有两点很值得注意。
第一,页面中meta标签的部分,常常可以见到
charset=GB2312
这样的写法,很不幸的是,这个“charset”其实是用来指定页面使用的是什么字符集编码,而不是使用什么字符集。例如你见到过有人写“charset=UTF-8”,见到过有人写“charset=ISO-8859-1”,但你见过有人写“charset=Unicode”么?当然没有,因为Unicode是一个字符集,而不是编码。
然而正是charset这个名称误导了很多程序员,真的以为这里要指定的是字符集,也因而使他们进一步的误以为UTF-8和UTF-16是一种字符集!(万恶啊)好在XML中已经做出了修改,这个位置改成了正确的名称:encoding。
第二,页面中说的GB2312,实际上并不真的是GB2312(惊讶么?)。我们来做个实验,例如找一个GB2312中不存在的汉字“亸”(这个字确实不在GB2312中,你可以到GB2312的码表中去找,保证找不到),这个字在GBK中。然后你把它放到一个html页面中,试着在浏览器中打开它,然后选择浏览器的编码为“GB2312”,看到了什么?它完全正常显示!
结论不用我说你也明白了,浏览器实际上使用的是GBK来显示。
新浪的页面中也有很多这样的例子,到处都写charset=GB2312,却使用了无数个GB2312中并不存在的字符。这种做法对浏览器显示页面并不成问题,但在需要程序抓取页面并保存的时候带来了麻烦,程序将不能依据页面所“声称”的编码进行读取和保存,而只能尽量猜测正确的编码。
需要再一次强调的是,无论历史上的UCS还是现如今的Unicode,两者指的都是编码字符集,而不是字符集编码。花费一点时间来理解好这件事,然后你会发现对所有网页的,系统的,编码标准之间的来回转换等等繁杂事务都会思路清晰,手到擒来。
首先说说最一般意义上的字符集。
一个抽象字符集其实就是指字符的集合,例如所有的英文字母是一个抽象字符集,所有的汉字是一个抽象字符集,当然,把全世界所有语言的符号都放在一起,也可以称为一个抽象字符集,所以这个划分是相当人为的。之所以说“抽象”二字,是因为这里所提及的字符不是任何具体形式的字符,拿汉字中的“汉”这个字符来说,您在这篇文章中看到的这个“汉”其实是这个字符的一种具体表现形式,是它的图像表现形式,而且它是用中文(而非拼音)书写而成,使用宋体外观;而当人们用嘴发出“汉”这个音的时候,他们是在使用“汉”的另一种具体表现形式——声音,但无论如何,两者所指的字符都是“汉”这个字。同一个字符的表现形式可能有无数种(点阵表示,矢量表示,音频表示,楷体,草书等等等等),把每一种表现形式下的同一个字符都纳入到字符集中,会使得集合过于庞大,冗余高,也不好管理。因此抽象字符集中的字符,都是指唯一存在的抽象字符,而忽略它的具体表现形式。
抽象字符集中的诸多字符,没有顺序之分,谁也不能说哪个字符在哪个字符前面,而且这种抽象字符只有人能理解。在给一个抽象字符集合中的每个字符都分配一个整数编号之后(注意这个整数并没有要求大小),这个字符集就有了顺序,就成为了编码字符集。同时,通过这个编号,可以唯一确定到底指的是哪一个字符。当然,对于同一个字符,不同的字符集所制定的整数编号也不尽相同,例如“儿”这个字,在Unicode中,它的编号是0x513F,(为方便起见,以十六进制表示,但这个整数编号并不要求必须是以十六进制表示)意思是说它是Unicode这个编码字符集中的第0x513F个字符。而在另一种编码字符集比如Big5中,这个字就是第0xA449个字符了。这种情况的另一面是,许多字符在不同的编码字符集中被分配了相同的整数编号,例如英文字母“A”,在ASCII及Unicode中,均是第0x41个字符。我们常说的Unicode字符集,指的就是这种被分配了整数编号的字符集合,但要澄清的是,编码字符集中字符被分配的整数编号,不一定就是该字符在计算机中存储时所使用的值,计算机中存储的字符到底使用什么二进制整数值来表示,是由下面将要说到的字符集编码决定的。
字符集编码决定了如何将一个字符的整数编号对应到一个二进制的整数值,有的编码方案简单的将该整数值直接作为其在计算机中的表示而存储,例如英文字符就是这样,几乎所有的字符集编码方案中,英文字母的整数编号与其在计算机内部存储的二进制形式都一致。但有的编码方案,例如适用于Unicode字符集的UTF-8编码形式,就将很大一部分字符的整数编号作了变换后存储在计算机中。以“汉”字为例,“汉”的Unicode值为0x6C49,但其编码为UTF-8格式后的值为0xE6B189(注意到变成了三个字节)。这里只是举个例子,关于UTF-8的详细编码规则可以参看《Mapping codepoints to Unicode encoding forms》一文,URL为http://scripts.sil.org/cms/scripts/page.php?site_id=nrsi&item_id=IWS-AppendixA#sec3。
我们经常听说的另一种编码方案UTF-16,则对Unicode中的前65536个字符编号都不做变换,直接作为计算机存储时使用的值(对65536以后的字符,仍然要做变换),例如“汉”字的Unicode编号为0x6C49,那么经过UTF-16编码后存储在计算机上时,它的表示仍为0x6C49!。我猜,正是因为UTF-16的存在,使得很多人认为Unicode是一种编码(实际上,是一个字符集,再次重申),也因此,很多人说Unicode的时候,他们实际上指的是UTF-16。UTF-16提供了surrogate pair机制,使得Unicode中码位大于65536的那些字符得以表示。
Surrogate pair机制在目前来说实在不常用,甚至连一些UTF-16的实现都不支持,所以我不打算在这里多加讨论,其基本的思想就是用两个16位的编码表示一个字符(注意,只对码位超过65536的字符这么做)。Unicode如此死抱着16这个数字不放,有历史的原因,也有实用的原因。
当然还有一种最强的编码,UTF-32,他对所有的Unicode字符均不做变换,直接使用编号存储!(俗称的以不变应万变),只是这种编码方案太浪费存储空间(就连1个字节就可以搞定的英文字符,它都必须使用4个字节),因而尽管使用起来方便(不需要任何转换),却没有得到普及。
记得当初Unicode与UCS还没成家之时,UCS也是需要人爱,需要人疼的,没有自己的字符集编码怎么成。UCS-2与UCS-4就扮演了这样的角色。UCS-4与UTF-32除了名字不同以外,思想完全一样。而UCS-2与UTF-16在对前65536个字符的处理上也完全相同,唯一的区别只在于UCS-2 不支持surrogate pair机制,即是说,UCS-2只能对前65536个字符编码,对其后的字符毫无办法。不过现在再谈起字符编码的时候,UCS-2与UCS-4早已成为计算机史学家才会用到的词汇,就让它们继续留在故纸堆里吧。
下一节我们来说说与中文相关的GB2312和GBK。
按:这是早前发表在我个人其他博客上的文章,现在根据文本分类和网页设计的需要进行重新的汇编和整理,也加入了一些新东西,希望对感兴趣的人有所帮助。
ASCII及相关标准
地球人都知道ASCII就是美国标准信息交换码的缩写,也知道ASCII规定用7位二进制数字来表示英文字符,ASCII被定为国际标准之后的代号为ISO-646。由于ASCII码只使用了7个二进制位,也就是说一个字节可以表示的256个数字中,它仅使用了0~127这128个码位,剩下的128个码位便可以用来做扩展,用来表示一些特定语言所独有的字符,因此对这多余的128个码位的不同扩展,就形成了一系列ISO-8859-*的标准。例如为英语作了专门扩展的字符集编码标准编号为ISO-8859-1,也叫做Latin-1,为希腊语所作的扩展编号为ISO-8859-7等,完整的列表可以参考《Java Internationalization》一书。
Unicode与UCS
整个Unicode项目是由多家计算机软件公司,还包括一些出版行业的公司共同发起的,从上世纪八十年代就已经开始。地球人都知道,对于日文,汉字来说,256个码位是远远不够用的(当然,在当时并不是地球人都知道,起码设计计算机的老美们就不知道,甚至直到今天,还有老美以为米国是世界上唯一的国家)。解决方法很直观也很明显,那就是采用码位多到足够包含所需字符数量的编码方案(即俗话说的头痛医头,脚痛医脚嘛)。这也是Unicode的目标之一,能够包含世界上所有语言的字符(包括汉字,日文,数学符号,音乐符号,还包括各种奇奇怪怪看也看不懂的东西比如象形文字,甲骨文 ,三个代表,科学发展观等等,笑),这个理想,可以说很远大,但很快被发现仅靠Unicode原先的设计无法实现。Unicode的另一个设计目标,对今天影响深远,那就是对所有字符都采用16位编码(即用一个大小不超过2的16次方的整数数字给每个字符编号,注意从这个意义上也可以看出,Unicode是一种编码字符集,而非字符集编码)。说这个设计目标对现今影响深远,完全不是表扬,因为到后来连Unicode的设计者也发现,16位编码仅有65536个码位,远远不能容纳世界上所有的字符,但当意识到这个问题的时候,Unicode大部分的规范已经制定完毕,也有相当程度的普及,完全推倒重来是不现实的。这成了一个遗留问题,也是surrogate pair这种蹩脚解决方案的发端。
无独有偶,在1984年,喜欢以繁多的编号糊弄群众的国际标准化组织ISO也开始着手制定解决不同语言字符数量太大问题的解决方案,这一方案被称为Universal Character Set(UCS),正式的编号是ISO-10646(记得么,ASCII是ISO-646,不知这种安排是否是故意的)。还是ISO高瞻远瞩,一开始就确定了UCS是一个31位的编码字符集(即用一个大小不超过2的31次方的整数数字为每个字符编号),这回真的足以容纳古往今来所有国家,所有语言所包含的字符了(是的,任何国家,任何小语种都包括,也不管这些国家是与台湾建交还是与中国大陆建交,是拥护民主制度还是实行恐怖主义,所以说科学无国界)。虽然后来他们意识到,2的31次方个码位又实在太多了……
天下大势,分久必合。无论Unicode还是UCS,最初的目的都是杜绝各种各样名目繁多形式各异互不兼容老死不相往来的私用扩展编码(好啰嗦的一句话),结果两方确立标准的同时(最初时这两个标准是不兼容的),又形成了割据,这对建设和谐社会是不利的,违反当今世界和平与发展的主旋律,中国政府一向反对任何形式的霸权主义和强权政治,对以米国为首的发达国家……扯远了扯远了。1991年,Unicode联盟与ISO的工作组终于开始讨论Unicode与UCS的合并问题,虽然其后的合并进行了很多年,Unicode初版规范中的很多编码都需要被改写,UCS也需要对码空间的使用进行必要限制,但成果是喜人的。最终,两者统一了抽象字符集(即任何一个在Unicode中存在的字符,在UCS中也存在),且最靠前的65535个字符也统一了字符的编码。对于码空间,两者同意以一百一十万为限(即两者都认为虽然65536不够,但2的31次方又太大,一百一十万是个双方都可接受的码空间大小,也够用,当然,这里说的一百一十万只是个约数),Unicode将码空间扩展到了一百一十万,而UCS将永久性的不使用一百一十万以后的码位。也就是说,现在再讲Unicode只包含65536个字符是不对的。除了对已经定义的字符进行统一外,Unicode联盟与ISO工作组也同意今后任何的扩展工作两者均保持同步,因此虽然从历史的意义上讲Unicode与UCS不是一回事(甚至细节上说也不是一回事),但现在提起Unicode,指代两者均无不妥。
使用开方检验能够修正文档频率作为特征选择手段的一些不足,在对复旦大学语料库作过一系列处理之后,为20个类别分别计算各自特征的开方值并排序(开方值越大则说明越应该作为特征被选中)之后,可以看出很多有意思的东西.记得在这一系列文章的part2中提到过仅仅使用词频来排序的时候,”个”这个词如明星般的在很多类别中都频繁出现在排名前十的位置上,但这个词实际上没有表意功能,对分类贡献不大,是理应被特征选择程序筛选掉的.使用开方检验方法后,我们惊喜的发现(读者:切!前人早都发现无数次了……):“个”消失了!
我稍微摘选结果中的几个类别在词频排序和开方值排序之间的比较,大家一起来瞅瞅。(前面也说过了,使用词频排序和使用文档频率情况大体相同,因此不再单独列出)
历史类别(History)
|
词频排序
|
开方值排序
|
|
历史 词频:24303
中国 词频:15146
人
词频:11707
社会 词频:8655
发展 词频:8540
研究 词频:8007
文化 词频:7607
大
词频:6748
新
词频:6706
到
词频:6537
说
词频:6462
种
词频:5694
问题 词频:5304
政治 词频:5178
文学 词频:5176
年
词频:4830
经济 词频:4810
思想 词频:4550
这种 词频:4476
个
词频:4276
|
近代史词频:350
史学
词频:2566
现代史词频:164
史料
词频:529
历史学词频:771
世界史词频:169
史实
词频:294
战争
词频:2095
封建
词频:1156
历史学词频:386
人物
词频:2399
统治
词频:1056
侵略
词频:501
记载
词频:625
历史
词频:24303
斗争
词频:1731
帝国主义词频:655
清政府词频:289
王朝
词频:370
民族
词频:4168
|
我列出了历史类文章中两种方法排名前二十的词汇,可以发现使用词频(或者文档频率)统计的结果纯粹无聊(简直无聊,特别无聊),除了“历史”,“社会”,“发展”听着还像那么回事以外,什么“说”,“种”,“年”这样的词真该统统杀光光。
用了开方检验就果然不一样,看看“史料”啊,“记载”呀,“王朝”呀,多正儿八经的历史词汇!我真是太喜欢开方检验啦!(笑)
当然结果也未必就十全十美了,我举个计算机的例子给你看。
计算机类别(Computer)
|
词频排序
|
开方值排序
|
|
系统词频:45496
控制词频:21937
图
词频:20396
方法词频:20073
个
词频:19661
算法词频:18879
数据词频:17691
模型词频:17182
网络词频:16980
进行词频:16406
问题词频:14617
应用词频:13883
对象词频:13656
信息词频:13468
结构词频:12658
研究词频:12308
实现词频:11331
过程词频:11293
设计词频:10713
种
词频:10506
|
算法
词频:18879
自动化词频:2674
计算机词频:7569
函数
词频:9932
定义
词频:9817
关键词词频:1956
软件
词频:6189
引言
词频:937
集合
词频:3717
输入
词频:6385
摘
词频:1540
定理
词频:4487
模型
词频:17182
用户
词频:10053
参数
词频:8491
导师
词频:969
向量
词频:2658
期
词频:213
输出
词频:6149
矩阵
词频:5431
|
看见”摘”这个词了么?居然出现在第11位,现在我还要告诉你,如果不是在去停止词的阶段把”要”字给去掉了,”要”字也会出现在”摘”附近的位置上,聪明的读者应该能大致猜出几分原因了吧.没错,到复旦语料库的计算机类文档中稍稍察看就会发现,大量的文档都有类似这样的格式:
计算机应用
COMPUTER APPLICATIONS
1999年第19卷第6期 Vol.19 No.6 1999
一种基于智能Agent的协同工作模型
朱晓芸 何钦铭 王申康
摘 要 计算机支持的协同工作(CSCW)需要研究出适应各种协同工作方式的灵活、开放、可扩充的模型结构。本文以分布式人工智能研究中的智能Agent为系统基本单元,提出一种基于智能Agent的协同工作模型,给出了它的具体实现。
关键词 计算机支持的协同工作,智能Agent,分布式人工智能
AN INTELLIGENT AGENT
BASED COLLABORATIVE WORK MODEL
Zhu XiaoyunHe QinmingWang Shenkang
看到”摘要”的位置了么?一来复旦语料库计算机类的文档大都是这类期刊文献的形式,因此”摘要”这个词频繁出现;二来其他类别的语料虽然也都有大量以文献作为来源的文档,但甚少用到”摘要”这个词;最后一点,注意到原文中”摘要”两个字是被空格分开的,只有我们这些地球的主宰者,全能的人类才能看出他们是一个词,而我们使用的分词程序会毫不留情的将其判断为”摘”和”要”两个词.这三点综合作用的结果,就使得我们的程序认为”摘”这个词对计算机类文档有很强的代表性(当然,我们自己心里知道,这纯属无稽之谈),从而入选了特征的TOP20。
以上分析给我们的启示是:作为训练集的文档来源一定要广泛,如果计算机类的文章还包括教科书,网页,个人博客的内容,显然就不会出现“摘”字这种笑话;另一方面,再一次重申,文本分类就应该是只依据文本的内容,而不应该包含文件的编码,文章格式,发表时间等外部信息,“摘”字的笑话多少也是因为文章的格式(在“摘”和“要”之间总有空格)影响了分词程序的判断而致。
关于复旦语料库所说的这些东西有点杂,有机会的话我会重新整理,再结合特征选择的具体方法,把特征选择的过程说说清楚。
以上。
开始之前首先说说分类体系。回忆一下,分类体系是指事先确定的类别的层次结构以及文档与这些类别间的关系。
其中包含着两方面的内容:
一,类别之间的关系。一般来说类别之间的关系都是可以表示成树形结构,这意味着一个类有多个子类,而一个子类唯一的属于一个父类。这种类别体系很常用,却并不代表它在现实世界中也是符合常识的,举个例子,“临床心理学”这个类别应该即属于“临床医学”的范畴,同时也属于“心理学”,但在分类系统中却不便于使用这样的结构。想象一下,这相当于类别的层次结构是一个有环图,无论遍历还是今后类别的合并,比较,都会带来无数的麻烦。
二,文档与类别间的关系。一般来说,在分类系统中,我们倾向于让一篇文档唯一的属于一个类别(更严格的说,是在同一层次中仅属于一个类别,因为属于一个类别的时候,显然也属于这个类别的父类别),这使得我们只适用一个标签就可以标记这个文档的类别,而一旦允许文档属于多个类别,标签的数目便成为大小不定的变量,难于设计成高效的数据结构。这种“属于多个”类的想法更糟的地方在于文档类别表示的语义方面,试想,如果姚明给灾区捐款的新闻即属于灾区新闻,也属于体育新闻的话(这在现实中倒确实是合情合理的),当用户使用这个系统来查找文档,指定的条件是要所有“属于灾区新闻但不属于体育新闻的新闻”(有点拗口,不过正好练嘴皮子啦,笑)的时候,这篇姚明的报道是否应该包含在查询结果中呢?这是一个矛盾的问题。
文本分类问题牵涉到如此多的主题,本身又含有如此多的属性,因此可以从多个角度对文本分类问题本身进行一下分类。
分类系统使用何种分类算法是分类系统的核心属性。如果一个分类算法在一次分类判断时,仅仅输出一个真假值用来表示待分类的文档是否属于当前类别的话,这样的系统就可以叫做基于二元分类器的分类系统。有些分类算法天然就是独立二元的,例如支持向量机,它只能回答这个文档是或不是这个类别的。这种分类算法也常常被称为“硬分类”的算法(Hard Categorization)。而有的算法在一次判断后就可以输出文档属于多个类别的得分(假设说,得分越大,则说明越有可能属于这个类别),这类算法称为“排序分类”的算法(Ranking Categorization),也叫做m元分类算法。kNN就是典型的m元分类算法(因为kNN会找出与待分类文档最相近的训练样本,并记录下这些样本所属的分类)。
摘要: 在上一篇文章中对复旦语料库进行分词,去停止词,去无用词性的词的基础上,再进行一次根据DF的处理,去除所有文档频率小于等于3的词,得到的对比结果如下 阅读全文
经过词频统计,看到复旦大学中文语料库的总词数为116558个(而且还是去掉了停止词及代词,介词,数词和时间短语等无关内容之后的结果),数量十分巨大.
而各个类别的词汇数量分别为:
类别名称:Agriculture 总文档数:1949 总词数:29163
类别名称:Art 总文档数:1237 总词数:40816
类别名称:Communication 总文档数:52 总词数:2283
类别名称:Computer 总文档数:2591 总词数:19340
类别名称:Economy 总文档数:2912 总词数:37021
类别名称:Education 总文档数:111 总词数:5719
类别名称:Electronics 总文档数:51 总词数:2693
类别名称:Energy 总文档数:63 总词数:2848
类别名称:Environment 总文档数:2347 总词数:25155
类别名称:History 总文档数:708 总词数:47205
类别名称:Law 总文档数:103 总词数:3834
类别名称:Literature 总文档数:65 总词数:5844
类别名称:Medical 总文档数:98 总词数:3877
类别名称:Military 总文档数:147 总词数:4615
类别名称:Mine 总文档数:63 总词数:3708
类别名称:Philosophy 总文档数:86 总词数:5190
类别名称:Politics 总文档数:1920 总词数:35292
类别名称:Space 总文档数:1226 总词数:14557
类别名称:Sports 总文档数:2344 总词数:42665
类别名称:Transport 总文档数:112 总词数:4644
很容易看出词汇的数量基本与类别包含的文档数成正比,但也有一些极其特殊的类别,比如艺术(Art)和历史(History),其文档数量仅有计算机文章数量的一半,但包含的词汇量却是计算机类别的两倍以上(分别是40816:19340和47205:19340,尤以历史类文章为甚,其文档数量仅有计算机类的三分之一还不到)。直观上的想法是,历史和艺术类文章包含了大量的人名,地名或者事件名等专有名词,因而词汇数量上表现得很巨大。计算机类文章包含词汇较少,一是因为其为新兴学科,包含的内容本就较少,另一个更重要的原因则在于前期对文章的处理忽略了所有的英文单词及缩写,而这些内容在计算机相关的文章中所占比重很大。
如果我们看整个语料库出现次数最多的十个词,会发现他们大致也是我们的国计民生所关注的几个方面(巧合?未必!)它们是:
词内容:经济 词性:名词 词频:233906 文档频率:8975
词内容:发展 词性:动词 词频:189181 文档频率:11847
词内容:农业 词性:名词 词频:126603 文档频率:4105
词内容:社会 词性:名词 词频:108988 文档频率:8686
词内容:政治 词性:名词 词频:106847 文档频率:4971
词内容:大 词性:形容词 词频:106111 文档频率:14729
词内容:中国 词性:名词 词频:105269 文档频率:10885
词内容:人 词性:名词 词频:98034 文档频率:11037
词内容:问题 词性:名词 词频:94458 文档频率:12538
词内容:个 词性:量词 词频:91717 文档频率:14428
通过与某些类别中排名前十位的词对比,我们可以看出很多问题,例如计算机类别:
词内容:系统 词性:形容词 词频:45496 文档频率:2244
词内容:控制 词性:动词 词频:21937 文档频率:1734
词内容:图 词性:名词 词频:20396 文档频率:1914
词内容:方法 词性:名词 词频:20073 文档频率:2141
词内容:个 词性:量词 词频:19661 文档频率:2207
词内容:算法 词性:名词 词频:18879 文档频率:1336
词内容:数据 词性:名词 词频:17691 文档频率:1357
词内容:模型 词性:名词 词频:17182 文档频率:1423
词内容:网络 词性:名词 词频:16980 文档频率:1159
词内容:进行 词性:动词 词频:16406 文档频率:2094
词内容:问题 词性:名词 词频:14617 文档频率:1965
再比如交通类别:
词内容:铁路 词性:名词 词频:280 文档频率:51
词内容:运输 词性:动词 词频:205 文档频率:74
词内容:交通 词性:名词 词频:158 文档频率:54
词内容:大 词性:形容词 词频:147 文档频率:59
词内容:工程 词性:名词 词频:136 文档频率:31
词内容:个 词性:量词 词频:117 文档频率:51
词内容:年 词性:量词 词频:114 文档频率:52
词内容:建设 词性:动词 词频:108 文档频率:40
词内容:公路 词性:名词 词频:106 文档频率:34
词内容:条 词性:量词 词频:105 文档频率:38
我们会发现,
第一:整个语料库出现最多的词未必在各个类别中也最多,实际上通过计算机和交通类别可以看出,几乎完全不同!这意味着在进行文本分类的训练阶段,针对各个类取不同的特征集合(即所谓local的特征选择)很有必要,如果所有的类别都使用相同的特征集合(而且毫无悬念的,这个特征集合就是语料库的特征集合),那么分类效果会因为没有为各个类找到最佳的特征而大打折扣;
第二,注意到“个”这个词出现在所有类别排名靠前的词汇中间,但直觉告诉我们,这个词很难对分类产生什么贡献(行话叫区分度很差)。此结论与信息论中所说的“一个词分布越广越均匀,则区分度越差”是一个意思。当然,在这里“个”会如明星般的出现在所有类别靠前的位置上,完全是因为我们的排名是根据词频来统计的(根据文档频率排序也会产生相似的结果),而使用像开方检验,信息增益这样的特征选择算法,就是为了避免这种区分度差的词出现在最终的特征集合中,从而影响分类效果。
在后续的文章里,我还会给出使用了开方检验计算特征得分以后的排名情况,“个”这个词会不会从前十名中消失呢?又有哪些词会冲上头排呢?我们拭目以待。(音乐响,幕布缓慢拉上,灯光渐暗)
复旦大学的中文语料库分为训练集和验证集两部分,两部分的文档数量基本相等,但现在做测评一般都不采用这种预先划分的方法,而多用交叉验证,因此在将训练集与验证集合并之后,得到该语料库的一些基本信息如下:
类别总数量:20
文档总数量:19637
类别名称(类别代码):文档数量
Agriculture(C32):2043篇
Art(C3):1482篇
Communication(C17):52篇
Computer(C19):2715篇
Economy(C34):3201篇
Education(C5):120篇
Electronics(C16):55篇
Energy(C15):65篇
Enviornment(C31):2435篇
History(C7):934篇
Law(C35):103篇
Literature(C4):67篇
Medical(C36):104篇
Military(C37):150篇
Mine(C23):67篇
Philosophy(C6):89篇
Politics(C38):2050篇
Space(C11):1282篇
Sports(C39):2507篇
Transport(C29):116篇
同时,在使用ictclas4j分词包对其进行分词的过程中,发现复旦语料库中存在一些文章会使得ictclas4j报错,其中因为分词包本身字库缺少某些文字,以及一些神秘的字符组合(确实很神秘)会导致分词过程出错,因此能够被成功分词而供后续使用的文档数并不如上面所列这么多,在分词之后,情况如下:
类别总数量:20
文档总数量:18185
类别名称(类别代码):文档数量
Agriculture(C32):1949篇
Art(C3):1237篇
Communication(C17):52篇
Computer(C19):2591篇
Economy(C34):2912篇
Education(C5):111篇
Electronics(C16):51篇
Energy(C15):63篇
Environment(C31):2347篇
History(C7):708篇
Law(C35):103篇
Literature(C4):65篇
Medical(C36):98篇
Military(C37):147篇
Mine(C23):63篇
Philosophy(C6):86篇
Politics(C38):1920篇
Space(C11):1226篇
Sports(C39):2344篇
Transport(C29):112篇
在已分词后的语料库里,可以看出这样几个特点,一,文档总数比未分词的版本少了1448篇(可见ictclas4j的错误还是满普遍的);第二,文档数量分布仍不均衡,最多的经济类文章有2912篇,而最少的电子类与通信类文章仅有51篇与52篇,往好的方向说可以考察你所开发的系统如何应对数据集偏斜的问题,往坏的方向说给要上线的系统作训练集恐怕不太合适。
在下一篇文章中,我将进一步总结词频统计的结果.
假设我们有以下的类别层次:
Layer1 --> Layer2 --> Layer3 --> Layer4
其中Layer1是位于最高位置的基类,Layer2是Layer1的直接子类,而Layer3又是Layer2的直接子类,等等.
我们在使用数组时会有这样的用法:
Layer1[] layerArray=new Layer2[10];
此时尽管运行时可能产生某些错误,例如往一个明明是Layer2的数组中加入一个Layer1的实例,但编译期并不会有什么问题.这是因为Java的数组存在称之为”协变”的现象,即如果Layer2是Layer1的子类,那么Layer2的数组也是Layer1的数组的子类.我们可以这样来验证:
Layer2[] layer2Array=new Layer2[10];
System.out.println(layer2Array
instanceof Layer1[]);
程序输出的结果为true.
像Layer1[] layerArray=new Layer2[10];这样写有一个很大的缺点,那就是你可以写
layerArray[0]=new Layer1();
这样的代码,编译器不会报错,但实际上我们往一个Layer2的数组里塞了一个Layer1的实例,这在运行时会扔出一个java.lang.ArrayStoreException。即是说数组没有提供编译期的类型检查。
而容器(例如List)很容易被我们认为是另一种数组,只是能够容纳各种类型以及动态改变大小而已。在JavaSE5之前,即使这样认为也不会给编程带来麻烦,因为容器没有办法指定所容纳的具体类型。但在引入泛型之后,我们可能为了编译期的类型检查以及动态改变大小两个理由而迫不及待的用容器彻底代替数组,也就有可能想当然的写出这样的代码:
List<Layer1> list=new ArrayList<Layer2>();
这样写的理由很简单,总是希望用基类型的引用来提供灵活性。然而遗憾的是,上述代码编译不能通过(或许编译期就不能通过这一点,反而是好事),原因就在于容器没有“协变”现象,一个Layer2的List并不是Layer1的List的子类,而是完全不同的类。因此上面的代码同
Integer i=new
String("你好");
一样荒谬,自然逃不过编译器的法眼。
难道就不能用泛型创建这样一种List的引用,类型参数只使用基类型,而在实例化的时候可以使用子类型,但又可以借助泛型的编译期检查么?
例如我想要一个List<Layer1>类型的引用,这个引用可以指向ArrayList<Layer2>或ArrayList<Layer4>(因为我不想关心实例化时的具体类型),但是一旦实例化一个ArrayList<Layer2>以后,又能借助编译器来检查向其中添加的确实是Layer2的实例,而非String或Integer。这能不能办到呢?
答案是不能,虽然初试之下,我们可能会利用泛型通配符想当然的写出如下代码:
List<? extends
Layer1> layer1List=new
ArrayList<Layer2>();
乍看之下,代码的本意是要建立一个泛型List的引用,而泛型的类别参数是任何Layer1的子类均可,这不正好合我们刚才所说的意思吗?而且这回编译器也没有报错,应该OK了吧!
接下来的事情却让人哭笑不得,这个List竟然不能添加任何元素,无论是写
layer1List.add(new Layer1());
还是写
layer1List.add(new Layer2());
均报错(编译期即错,不用待到运行时)。甚至是
layer1List.add(new Object());
也报错(这证明了无论提供的类型参数是Layer1的子类还是超类,亦或者Layer1本身,均报错)。
这是为什么呢?(给读者3分钟思考,然后带着诡异的微笑揭晓答案)
原来extends关键字圈定的是泛型参数的上界,回头单看
List<? extends
Layer1>
这一句,其实说的是,我有一个泛型的List,它的类别参数是Layer1的一个子类,因此如果这个子类是Layer3,那么Layer2以上的类别就不能向该List中添加(这个没什么问题吧,别绕进去了哦),如果这个子类别是Layer4,那么Layer3以上的类别就不能向该List中添加(想象我们的类别体系还存在Layer5,Layer6等等,显然子类别是哪一个都有可能,那就是说拒绝任何一个类别都是说得通的)。因此编译器根本无法确定这个List到底可以放什么不可以放什么,所以统统拒绝。
更正式一点说,extends给了一个上界,只有该界以下的类别才能合法的添加到List中,但是这个上界本身都是不确定的(它可以无限往类别体系的下方移动),自然也就说不出哪些类别是合法的了。
结论:想要容器提供类似于数组那样的协变效果,而又要有类型检查,至少在我所知范围,办不到。
自从有了范型,Java的容器操作便利了不少,但因为还存在int,float这里原始数据类型而磨合得还不够好.
例如下面的这个小例子:
Map<String,Integer> map=new HashMap<String,Integer>();
map.put("1",1);
System.out.println(map.get("2"));
实际上map中并没有键为"2"的值,不过代码运行正常,输出为
null
现在来做一点小改动,
Map<String,Integer> map=new HashMap<String,Integer>();
map.put("1",1);
int i=map.get("2");
System.out.println(i);
注意到只是用中间变量i暂时存放了一下取出的值,这个时候就会报错啦:
Exception in thread "main" java.lang.NullPointerException
仔细想想倒也觉得错得在理,因为不存在的对象可以以null来表示,但不存在的数字在Java中却没有对应的表示(例如Ruby中就有NAN,表示这不是一个数字)。乍看之下好像也没什么大不了,但是这样的小缺陷使得在Java编程中想像一般类型一样的来使用数字和容器变得不太可能,如果用一个容器来做数字的存取,则只能在取之前很小心的先查看使用的键值对是否已经在容器中,而不能像一般对象的存取那样,直接取出,通过结果来判断罢了。
发现这个小纰漏仅在偶然间,JDK的文档我看得不多,也许SUN的工程师早就在哪里提醒过大家了吧,只是我孤陋寡闻而已,大家看着玩玩。
ICTCLAS是中科院计算所出品的中文分词程序包,在国内一直有着良好的口碑和很高的使用率。之前一直只有 C++的版本提供,而现在C#,Delphi和Java版本已经纷纷出炉。下面用一个极小的例子,让大家10分钟之内就能用上ICTCLAS ,从此也开始自己的文本分类和搜索引擎开发之路。
需要首先说明的是,不同于以前的C++版提供的JNI调用,本次使用的是纯Java版本的ICTCLAS,下载地址在http://ictclas.org/Down_OpenSrc.asp。
好,假设你已经下载了我们需要使用的Java版本ictclas4j,现在把它解压缩,然后把Data文件夹整个拷贝到Eclipse项目的文件夹下,而bin目录下的org文件夹整个拷贝到你Eclipse项目的bin目录下,把src目录下的org文件夹整个拷贝到Eclipse项目的src目录下(最简单快捷的使用方式,或者你自己打成jar包,这样无论放到哪里,都可以在build
path里面导入这个jar包啦)。
现在就可以在你的项目里新建一个类来试试。我新建了一个类,代码如下:
import
org.ictclas4j.bean.SegResult;
import
org.ictclas4j.segment.SegTag;
public class OneMain {
public static void main(String[] args) {
System.out.println("This is OneMain");
SegTag
st = new SegTag(1);
SegResult
sr = st
.split("一块勤奋地漂亮的一块钱,/打造经济的航空母舰。ABCD.#$% Hello World!\n又一段文本123辆 !3.0");
System.out.println(sr.getFinalResult());
}
}
很显然文本“一块勤奋地漂亮的一块钱,/打造经济的航空母舰。ABCD.#$%
Hello World!"n又一段文本123辆 !3.0”就是我们用来测试的文本,其中包含了中文,英文,标点符号,乱七八糟符号(笑)及阿拉伯数字。
我们运行刚才的程序,看下输出结果:
This is
OneMain
一块/s 勤奋/a 地/u 漂亮/a 的/u 一/m 块/q 钱/n
,/w //nx 打造/v 经济/n 的/u 航空母舰/n 。/w
ABCD.#$%/nx Hello/nx World/nx !/w 又/d 一/m 段/q 文本/n
123/m 辆/q
看到了么,分词的结果是一个长长的String类数据,用空格区分出每个词,每个词还用/后面的英文标号标出了词性。一起来看看几个有趣的地方。
原文中其实有两个“一块”,一处是“一块勤奋”,这里很正确的识别为了副词,而后面的“一块钱”中的“一块”也正确的识别为数量词。
阿拉伯数字正确识别为数词,包括小数形式的“3.0”。而英文和乱七八糟符号(包括那个不可见的换行符,你找到它在哪了吗?)则都被划为一类——/nx!(因为我也不知道ICTCLAS内部人员管它叫什么啦,非法字符啊,还是无效字符啊,或者其它字符啊,名字可以自己取嘛)
测试文本中还有两个叹号,一个是英文半角的!,一个是中文全角的!,两者也都被正确识别为标点符号,但英文的句号“.“就被认为是/nx啦。
测试文本中的空格被完全忽略。
好,十分简单对不对?去玩玩吧。
在系列文章《SVM入门(三)》中论述间隔的重要性之时,由于疏忽和大意有一处不明确和一处错误。
于该部分我曾经提到过
“之所以如此关心间隔这个东西,是因为间隔与样本的误分次数间存在关系:

”
此处更确切的说法应该是几何间隔与样本的误分次数存在上述关系。
就在刚才这段话的下面,我解释R代表的含义时说它是“R是空间中一个能完全包含样本数据的球的半径”,很遗憾这是错误的,正确的定义是
R=max ||xi|| i=1,...,n
即R是所有样本中(xi是以向量表示的第i个样本)向量长度最长的值。
犯下上述错误,委实显得不专业,在此道歉。
前文提到过,除了分类算法以外,为分类文本作处理的特征提取算法也对最终效果有巨大影响,而特征提取算法又分为特征选择和特征抽取两大类,其中特征选择算法有互信息,文档频率,信息增益,开方检验等等十数种,这次先介绍特征选择算法中效果比较好的开方检验方法。
大家应该还记得,开方检验其实是数理统计中一种常用的检验两个变量独立性的方法。(什么?你是文史类专业的学生,没有学过数理统计?那你做什么文本分类?在这捣什么乱?)
开方检验最基本的思想就是通过观察实际值与理论值的偏差来确定理论的正确与否。具体做的时候常常先假设两个变量确实是独立的(行话就叫做“原假设”),然后观察实际值(也可以叫做观察值)与理论值(这个理论值是指“如果两者确实独立”的情况下应该有的值)的偏差程度,如果偏差足够小,我们就认为误差是很自然的样本误差,是测量手段不够精确导致或者偶然发生的,两者确确实实是独立的,此时就接受原假设;如果偏差大到一定程度,使得这样的误差不太可能是偶然产生或者测量不精确所致,我们就认为两者实际上是相关的,即否定原假设,而接受备择假设。
那么用什么来衡量偏差程度呢?假设理论值为E(这也是数学期望的符号哦),实际值为x,如果仅仅使用所有样本的观察值与理论值的差值x-E之和
来衡量,单个的观察值还好说,当有多个观察值x1,x2,x3的时候,很可能x1-E,x2-E,x3-E的值有正有负,因而互相抵消,使得最终的结果看上好像偏差为0,但实际上每个都有偏差,而且都还不小!此时很直接的想法便是使用方差代替均值,这样就解决了正负抵消的问题,即使用
这时又引来了新的问题,对于500的均值来说,相差5其实是很小的(相差1%),而对20的均值来说,5相当于25%的差异,这是使用方差也无法体现的。因此应该考虑改进上面的式子,让均值的大小不影响我们对差异程度的判断
 式(1) 式(1)
上面这个式子已经相当好了。实际上这个式子就是开方检验使用的差值衡量公式。当提供了数个样本的观察值x1,x2,……xi ,……xn之后,代入到式(1)中就可以求得开方值,用这个值与事先设定的阈值比较,如果大于阈值(即偏差很大),就认为原假设不成立,反之则认为原假设成立。
在文本分类问题的特征选择阶段,我们主要关心一个词t(一个随机变量)与一个类别c(另一个随机变量)之间是否相互独立?如果独立,就可以说词t对类别c完全没有表征作用,即我们根本无法根据t出现与否来判断一篇文档是否属于c这个分类。但与最普通的开方检验不同,我们不需要设定阈值,因为很难说词t和类别c关联到什么程度才算是有表征作用,我们只想借用这个方法来选出一些最最相关的即可。
此时我们仍然需要明白对特征选择来说原假设是什么,因为计算出的开方值越大,说明对原假设的偏离越大,我们越倾向于认为原假设的反面情况是正确的。我们能不能把原假设定为“词t与类别c相关“?原则上说当然可以,这也是一个健全的民主主义社会赋予每个公民的权利(笑),但此时你会发现根本不知道此时的理论值该是多少!你会把自己绕进死胡同。所以我们一般都使用”词t与类别c不相关“来做原假设。选择的过程也变成了为每个词计算它与类别c的开方值,从大到小排个序(此时开方值越大越相关),取前k个就可以(k值可以根据自己的需要选,这也是一个健全的民主主义社会赋予每个公民的权利)。
好,原理有了,该来个例子说说到底怎么算了。
比如说现在有N篇文档,其中有M篇是关于体育的,我们想考察一个词“篮球”与类别“体育”之间的相关性(任谁都看得出来两者很相关,但很遗憾,我们是智慧生物,计算机不是,它一点也看不出来,想让它认识到这一点,只能让它算算看)。我们有四个观察值可以使用:
1.
包含“篮球”且属于“体育”类别的文档数,命名为A
2.
包含“篮球”但不属于“体育”类别的文档数,命名为B
3.
不包含“篮球”但却属于“体育”类别的文档数,命名为C
4.
既不包含“篮球”也不属于“体育”类别的文档数,命名为D
用下面的表格更清晰:
|
特征选择
|
1.属于“体育”
|
2.不属于“体育”
|
总 计
|
|
1.包含“篮球”
|
A
|
B
|
A+B
|
|
2.不包含“篮球”
|
C
|
D
|
C+D
|
|
总 数
|
A+C
|
B+D
|
N
|
如果有些特点你没看出来,那我说一说,首先,A+B+C+D=N(这,这不废话嘛)。其次,A+C的意思其实就是说“属于体育类的文章数量”,因此,它就等于M,同时,B+D就等于N-M。
好,那么理论值是什么呢?以包含“篮球”且属于“体育”类别的文档数为例。如果原假设是成立的,即“篮球”和体育类文章没什么关联性,那么在所有的文章中,“篮球”这个词都应该是等概率出现,而不管文章是不是体育类的。这个概率具体是多少,我们并不知道,但他应该体现在观察结果中(就好比抛硬币的概率是二分之一,可以通过观察多次抛的结果来大致确定),因此我们可以说这个概率接近
(因为A+B是包含“篮球”的文章数,除以总文档数就是“篮球”出现的概率,当然,这里认为在一篇文章中出现即可,而不管出现了几次)而属于体育类的文章数为A+C,在这些个文档中,应该有
篇包含“篮球”这个词(数量乘以概率嘛)。
但实际有多少呢?考考你(读者:切,当然是A啦,表格里写着嘛……)。
此时对这种情况的差值就得出了(套用式(1)的公式),应该是
同样,我们还可以计算剩下三种情况的差值D12,D21,D22,聪明的读者一定能自己算出来(读者:切,明明是自己懒得写了……)。有了所有观察值的差值,就可以计算“篮球”与“体育”类文章的开方值
把D11,D12,D21,D22的值分别代入并化简,可以得到
词t与类别c的开方值更一般的形式可以写成
 式(2) 式(2)
接下来我们就可以计算其他词如“排球”,“产品”,“银行”等等与体育类别的开方值,然后根据大小来排序,选择我们需要的最大的数个词汇作为特征项就可以了。
实际上式(2)还可以进一步化简,注意如果给定了一个文档集合(例如我们的训练集)和一个类别,则N,M,N-M(即A+C和B+D)对同一类别文档中的所有词来说都是一样的,而我们只关心一堆词对某个类别的开方值的大小顺序,而并不关心具体的值,因此把它们从式(2)中去掉是完全可以的,故实际计算的时候我们都使用
 式(3) 式(3)
好啦,并不高深对不对?
针对英文纯文本的实验结果表明:作为特征选择方法时,开方检验和信息增益的效果最佳(相同的分类算法,使用不同的特征选择算法来得到比较结果);文档频率方法的性能同前两者大体相当,术语强度方法性能一般;互信息方法的性能最差(文献[17])。
但开方检验也并非就十全十美了。回头想想A和B的值是怎么得出来的,它统计文档中是否出现词t,却不管t在该文档中出现了几次,这会使得他对低频词有所偏袒(因为它夸大了低频词的作用)。甚至会出现有些情况,一个词在一类文章的每篇文档中都只出现了一次,其开方值却大过了在该类文章99%的文档中出现了10次的词,其实后面的词才是更具代表性的,但只因为它出现的文档数比前面的词少了“1”,特征选择的时候就可能筛掉后面的词而保留了前者。这就是开方检验著名的“低频词缺陷“。因此开方检验也经常同其他因素如词频综合考虑来扬长避短。
好啦,关于开方检验先说这么多,有机会还将介绍其他的特征选择算法。
附:给精通统计学的同学多说几句,式(1)实际上是对连续型的随机变量的差值计算公式,而我们这里统计的“文档数量“显然是离散的数值(全是整数),因此真正在统计学中计算的时候,是有修正过程的,但这种修正仍然是只影响具体的开方值,而不影响大小的顺序,故文本分类中不做这种修正。
上回说到对于文本分类这样的不适定问题(有一个以上解的问题称为不适定问题),需要有一个指标来衡量解决方案(即我们通过训练建立的分类模型)的好坏,而分类间隔是一个比较好的指标。
在进行文本分类的时候,我们可以让计算机这样来看待我们提供给它的训练样本,每一个样本由一个向量(就是那些文本特征所组成的向量)和一个标记(标示出这个样本属于哪个类别)组成。如下:
Di=(xi,yi)
xi就是文本向量(维数很高),yi就是分类标记。
在二元的线性分类中,这个表示分类的标记只有两个值,1和-1(用来表示属于还是不属于这个类)。有了这种表示法,我们就可以定义一个样本点到某个超平面的间隔:
δi=yi(wxi+b)
这个公式乍一看没什么神秘的,也说不出什么道理,只是个定义而已,但我们做做变换,就能看出一些有意思的东西。
首先注意到如果某个样本属于该类别的话,那么wxi+b>0(记得么?这是因为我们所选的g(x)=wx+b就通过大于0还是小于0来判断分类),而yi也大于0;若不属于该类别的话,那么wxi+b<0,而yi也小于0,这意味着yi(wxi+b)总是大于0的,而且它的值就等于|wxi+b|!(也就是|g(xi)|)
现在把w和b进行一下归一化,即用w/||w||和b/||w||分别代替原来的w和b,那么间隔就可以写成
![clip_image002[28]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVMPart2_C019/clip_image002%5B28%5D_thumb.gif)
这个公式是不是看上去有点眼熟?没错,这不就是解析几何中点xi到直线g(x)=0的距离公式嘛!(推广一下,是到超平面g(x)=0的距离, g(x)=0就是上节中提到的分类超平面)
小Tips:||w||是什么符号?||w||叫做向量w的范数,范数是对向量长度的一种度量。我们常说的向量长度其实指的是它的2-范数,范数最一般的表示形式为p-范数,可以写成如下表达式
向量w=(w1, w2, w3,…… wn)
它的p-范数为
![clip_image004[10]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVMPart2_C019/clip_image004%5B10%5D_thumb.gif)
看看把p换成2的时候,不就是传统的向量长度么?当我们不指明p的时候,就像||w||这样使用时,就意味着我们不关心p的值,用几范数都可以;或者上文已经提到了p的值,为了叙述方便不再重复指明。
当用归一化的w和b代替原值之后的间隔有一个专门的名称,叫做几何间隔,几何间隔所表示的正是点到超平面的欧氏距离,我们下面就简称几何间隔为“距离”。以上是单个点到某个超平面的距离(就是间隔,后面不再区别这两个词)定义,同样可以定义一个点的集合(就是一组样本)到某个超平面的距离为此集合中离超平面最近的点的距离。下面这张图更加直观的展示出了几何间隔的现实含义:
![clip_image010[10]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVMPart2_C019/clip_image010%5B10%5D_thumb.gif)
H是分类面,而H1和H2是平行于H,且过离H最近的两类样本的直线,H1与H,H2与H之间的距离就是几何间隔。
之所以如此关心间隔这个东西,是因为间隔与样本的误分次数间存在关系:

其中的δ是样本集合到分类面的间隔,R是空间中一个能完全包含样本数据的球的半径(也就是说代表样本的分布有多么广)。先不必追究误分次数的具体定义和推导过程,只要记得这个误分次数一定程度上代表分类器的误差。而从上式可以看出,误分次数的上界由间隔决定!(当然,是样本已知的时候)
至此我们就明白为何要选择间隔来作为评价一个解优劣的指标了,原来间隔越大的解,它的误差上界越小。因此最大化间隔成了我们训练阶段的目标,而且,与二把刀作者所写的不同,最大化分类间隔并不是SVM的专利,而是早在线性分类时期就已有的思想。
但是看过一些关于SVM的论文的人一定记得什么优化的目标是要最小化||w||这样的说法,这是怎么回事呢?回头再看看
![clip_image006[11]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVMPart2_C019/clip_image006%5B11%5D_thumb.gif)
这个公式,这里的|g(x)|代表样本集到超平面g(x)=0距离最近的点的值,因此是一个定值,注意到间隔与||w||是成反比的,因此最大化间隔与最小化||w||完全是一回事。而我们常用的方法并不是固定||w||的大小而寻求最大间隔,而是固定间隔(例如固定为1),寻找最小的||w||。
现在有了一个线性分类函数,也有了判断解优劣的标准(有了优化的目标),接下来自然关心如何求解,且听下回分解。
线性分类器(一定意义上,也可以叫做感知机) 是最简单也很有效的分类器形式.在一个线性分类器中,可以看到SVM形成的思路,并接触很多SVM的核心概念. 用一个二维空间里仅有两类样本的分类问题来举个小例子。如图所示 
C1和C2是要区分的两个类别,在二维平面中它们的样本如上图所示。中间的直线就是一个分类函数,它可以将两类样本完全分开。一般的,如果一个线性函数能够将样本完全正确的分开,就称这些数据是线性可分的,否则称为非线性可分的。 什么叫线性函数呢?在一维空间里就是一个点,在二维空间里就是一条直线,三维空间里就是一个平面,可以如此想象下去,如果不关注空间的维数,这种线性函数还有一个统一的名称——超平面(Hyper Plane)! 实际上,一个线性函数是一个实值函数(即函数的值是连续的实数),而我们的分类问题(例如这里的二元分类问题——回答一个样本属于还是不属于一个类别的问题)需要离散的输出值,例如用1表示某个样本属于类别C1,而用0表示不属于(不属于C1也就意味着属于C2),这时候只需要简单的在实值函数的基础上附加一个阈值即可,通过分类函数执行时得到的值大于还是小于这个阈值来确定类别归属。 例如我们有一个线性函数 g(x)=wx+b 我们可以取阈值为0,这样当有一个样本xi需要判别的时候,我们就看g(xi)的值。若g(xi)>0,就判别为类别C1,若g(xi)<0,则判别为类别C2(等于的时候我们就拒绝判断,呵呵)。此时也等价于给函数g(x)附加一个符号函数sgn(),即f(x)=sgn [g(x)]是我们真正的判别函数。 关于g(x)=wx+b这个表达式要注意三点:一,式中的x不是二维坐标系中的横轴,而是样本的向量表示,例如一个样本点的坐标是(3,8),则xT=(3,8) ,而不是x=3(一般说向量都是说列向量,因此以行向量形式来表示时,就加上转置)。二,这个形式并不局限于二维的情况,在n维空间中仍然可以使用这个表达式,只是式中的w成为了n维向量(在二维的这个例子中,w是二维向量,注意这里的w严格的说也应该是转置的形式,为了表示起来方便简洁,以下均不区别列向量和它的转置,聪明的读者一看便知);三,g(x)不是中间那条直线的表达式,中间那条直线的表达式是g(x)=0,即wx+b=0,我们也把这个函数叫做分类面。 实际上很容易看出来,中间那条分界线并不是唯一的,我们把它稍微旋转一下,只要不把两类数据分错,仍然可以达到上面说的效果,稍微平移一下,也可以。此时就牵涉到一个问题,对同一个问题存在多个分类函数的时候,哪一个函数更好呢?显然必须要先找一个指标来量化“好”的程度,通常使用的都是叫做“分类间隔”的指标。下一节我们就仔细说说分类间隔,也补一补相关的数学知识。
|
|
| | 日 | 一 | 二 | 三 | 四 | 五 | 六 |
|---|
| 29 | 30 | 1 | 2 | 3 | 4 | 5 | | 6 | 7 | 8 | 9 | 10 | 11 | 12 | | 13 | 14 | 15 | 16 | 17 | 18 | 19 | | 20 | 21 | 22 | 23 | 24 | 25 | 26 | | 27 | 28 | 29 | 30 | 31 | 1 | 2 | | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|
公告
邮箱:zhenandaci@msn.com
常用链接
留言簿(64)
随笔分类
随笔档案
文章分类
搜索
最新评论

阅读排行榜
评论排行榜
|
|