继续上一篇的探讨,对于有向无环图我们可以通过动态规划解决,那么对于有向有环图呢?这里列出一个例子解决 有向有环图的动态规划解。
如前所述,在解决图路径的动态规划问题时,我们递归或者迭代求解,列出DPFE方程。这里仍旧拿上一个例子来说,为了把无环变为有环,加一条边(y,x)=2,并且假设图是没有自循环节点的,也就是节点不能到达自己。这样问题就变为一个经典的Shortest Path in Cyclic Graph(SPC)——我们讨论的第三个动态规划问题,图形如下:
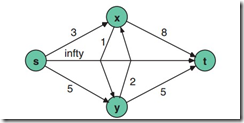
如果依旧像之前一样列方程,会发现,f(x)=min{b(x,y)+f(y), b(x,t)+f(t)},f(y)=min{b(y,x)+f(x),b(y,t)+f(t)},这里两个方程f(x)和f(y)互相依赖,无法直接求解。为此,要引入一种叫做“松弛”(relaxation)的技术,当我们想求一个数列x*=min{a1,a2,…,aN}的最小值时,可以把它等价为x*=min{min{…min{a1,a2},a3},…},aN}。我们把一个全局问题降级成了处理一系列两个元素的比较问题引入了一系列xi变量,令x1=a1,那么x2=min{x1,a2},x3=min{x2,a3},……依次得到递归解xi=min{x(i-1),ai},其中i>0,且初始条件x1=a1,不过一般为了一致性,我们多定义一个x0=∞,这样x1=min{x0,a1}。那么松弛带来的第一个表示方法就是对于常规问题S={x1,x2,…,xm},Sx’代表在选择了x后的下一个状态,成本函数还是C(x|S),表示f(S)=min{min{…min{C(x1|S)+f(Sx1’),C(x2|S)+f(Sx2’)},…},C(xm|S)+f(Sxm’)},使用这种表示方法解决问题,需要先把S的元素排序,f(Sxi’)需要先被预先计算出来。换种思路用stage decision阶段决策来看松弛,那么结果就是f(k,S)=min x{C(x|k,s)+f(k-1,Sx’)},对于每个S都要计算一个序列f(0,S),f(1,S)…来逼近f(S),这个序列的最小值就是问题的解即f(S)=min{f(k,S)}。可以看出f(k,S)并不单调,所以还需要全局再求一次最值,所以松弛会再定义一个F(k,S),使得F(k,S)=min{F(k-1,S), min{C(x|k,S)+F(k-1,Sx’)}},这样一来,函数变为单调,且在f(S)收敛。
回到SPC问题,因为普通方程出现了互相依赖,因此利用松弛技术,我们把依赖化解掉,利用第一种渐进逼近法,我们先定义f(s)=f(x)=f(y)=∞,f(t)=0,这时第一轮迭代,f(s)=min{3+∞,5+∞,∞+0}=∞,f(x)=min{1+∞, 8+0}=8,f(y)=min{2+∞,5+0}=5,f(t)=0,这样,就把本来互相依赖的f(x)和f(y)化解了死锁,让他们有了初始值,接下来继续迭代,f(s)=min{3+8, 5+5, ∞+0}=10,f(x)=min{1+5,8+0}=6,f(y)=min{2+8,5+0}=5,f(t)=0,最后迭代f(s)=min{3+6,5+5,∞+0}=9,得到最终解。
利用第二种阶段决策方法,有f(k,p)=min q{b(p,q)+f(k-1,q)},f(k,p)表示从p到终点的最短路径长度,路径有k段。基础条件是f(0,t)=0,f(0,p)=∞当p≠t,f(k,t)=∞当k>0,于是第一轮迭代,f(1,s)=min{3+f(0,x),5+f(0,y),∞+f(0,t)}=∞,f(1,x)=min{1+f(0,y),8+f(0,t)}=8,f(1,y)=min{2+f(0,x),5+f(0,t)}=5,f(1,t)=∞;第二轮迭代,f(2,s)=min{3+f(1,x),5+f(1,y),∞+f(1,t)}=10,f(2,x)=min{1+f(1,y),8+f(1,t)}=6,f(2,y)=min{2+f(1,x),5+f(1,t)}=10,f(2,t)=∞;最后迭代,f(3,s)=min{3+f(2,x),5+f(2,y),∞+f(2,t)}=9,f(3,x)=min{1+f(2,y),8+f(2,t)}=11,f(3,y)=min{2+f(2,x),5+f(2,t)}=8,f(3,t)=∞;最后计算f(s)=min{f(0,s),f(1,s),f(2,s),f(3,s)}=min{∞,∞,10,9}=9,f(x)=min{∞,8,6,11}=6,f(y)=min{∞,5,10,8}=5,f(t)=min{0,∞,∞,∞}=0。
阶段决策需要再求一次最值,且迭代求出了所有解,这并不优雅,使用第三种方法——真正的松弛技术:定义F(k,p)是从p到t的最短路径长度,由k或更少段路径组成。那么目标可以等价于F(N-1,s),基本条件是F(0,t)=0,F(0,p)=∞当p≠t,F(k,t)=∞当k>0,DPFE为F(k,p)=min q{b(p,q)+F(k-1,q)},松弛后的形式为F(k,p)=min{min{…min{b(p,q1)+F(k-1,q1),b(p,q2)+F(k-1,q2)},…},b(p,qm)+F(k-1,qm)}。这种松弛技术也是Bellman-Ford算法的基础,Bellman-Ford算法可以求出从单一节点到所有其他节点的最短路,思路就是不断松弛,计算从起点开始到其他节点的最短路径。同时还有Floyd-Warshall算法,依据松弛技术,求得图模型里的所有节点对的最短路径,时间复杂度O(n3),空间复杂度O(n2)。这两种算法可以参看《算法导论》或者wikipedia,这里不再详述。
source code:DPFE
1: /*
2: * Copyright (C) 2013 changedi
3: *
4: * Licensed under the Apache License, Version 2.0 (the "License");
5: * you may not use this file except in compliance with the License.
6: * You may obtain a copy of the License at
7: *
8: * http://www.apache.org/licenses/LICENSE-2.0
9: *
10: * Unless required by applicable law or agreed to in writing, software
11: * distributed under the License is distributed on an "AS IS" BASIS,
12: * WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
13: * See the License for the specific language governing permissions and
14: * limitations under the License.
15: */
16: package com.jybat.dp;
17:
18: import java.util.HashSet;
19: import java.util.Set;
20:
21: public class ShortestPathCyclic { 22:
23: private static final int INF = Integer.MAX_VALUE;
24:
25: private static Set<Integer> path = new HashSet<Integer>();
26: // nodes (s,x,y,t) = {0,1,2,3}, so (s,x) = 3 means d[0][1] = 3 27: private static int[][] distance = { 28: { INF, 5, 3, INF }, 29: { INF, INF, 2, 5 }, 30: { INF, 1, INF, 8 }, 31: { INF, INF, INF, INF } 32: };
33:
34: private static Set<Integer> possibleNextNodes(int node) { 35: Set<Integer> result = new HashSet<Integer>();
36: for (int i = 0; i < distance[node].length; i++) { 37: if (distance[node][i] != INF) { 38: result.add(new Integer(i));
39: }
40: }
41: return result;
42: }
43:
44: public static double f(int currentNode, Set<Integer> nodesVisited){ 45: if(currentNode==3) return 0.0;
46: else{ 47: Set<Integer> possibleSuccessors = possibleNextNodes(currentNode);
48: possibleSuccessors.removeAll(nodesVisited);
49: double min = Double.MAX_VALUE;
50: for(Integer a : possibleSuccessors){ 51: Set<Integer> set = new HashSet<Integer>();
52: set.addAll(nodesVisited);
53: set.add(a);
54: double dis = distance[currentNode][a]+f(a,set);
55: if(dis<min) { 56: min = dis;
57: }
58: }
59: return min;
60: }
61: }
62:
63: /**
64: * @param args
65: */
66: public static void main(String[] args) { 67: path.add(0);
68: double shortest = f(0,path);
69: System.out.println(shortest);
70: }
71:
72: }
source code:松弛法
1: /*
2: * Copyright (C) 2013 changedi
3: *
4: * Licensed under the Apache License, Version 2.0 (the "License");
5: * you may not use this file except in compliance with the License.
6: * You may obtain a copy of the License at
7: *
8: * http://www.apache.org/licenses/LICENSE-2.0
9: *
10: * Unless required by applicable law or agreed to in writing, software
11: * distributed under the License is distributed on an "AS IS" BASIS,
12: * WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
13: * See the License for the specific language governing permissions and
14: * limitations under the License.
15: */
16: package com.jybat.dp;
17:
18: import java.util.HashSet;
19: import java.util.Set;
20:
21: public class ShortestPathCyclic2 { 22:
23: private static final int INF = Integer.MAX_VALUE;
24:
25: // nodes (s,x,y,t) = {0,1,2,3}, so (s,x) = 3 means d[0][1] = 3 26: private static int[][] distance = { 27: { INF, 5, 3, INF }, 28: { INF, INF, 2, 5 }, 29: { INF, 1, INF, 8 }, 30: { INF, INF, INF, INF } 31: };
32:
33: private static Set<Integer> possibleNextNodes(int node) { 34: Set<Integer> result = new HashSet<Integer>();
35: for (int i = 0; i < distance[node].length; i++) { 36: if (distance[node][i] != INF) { 37: result.add(new Integer(i));
38: }
39: }
40: return result;
41: }
42:
43: public static double f(int currentNode, int noOfEdgesToTarget){ 44: if(currentNode==3)
45: return 0.0;
46: else if(noOfEdgesToTarget==0&¤tNode!=3)
47: return INF;
48: else{ 49: Set<Integer> possibleSuccessors = possibleNextNodes(currentNode);
50: double min = Double.MAX_VALUE;
51: for(Integer d : possibleSuccessors){ 52: double dis = distance[currentNode][d]+f(d,noOfEdgesToTarget-1);
53: if(dis<min) { 54: min = dis;
55: }
56: }
57: return min;
58: }
59: }
60:
61: /**
62: * @param args
63: */
64: public static void main(String[] args) { 65: double shortest = f(0,3);
66: System.out.println(shortest);
67: }
68:
69: }