影响空间规模的几种数据存储结构
正文
所谓数据存储结构,就是数据的元素与元素之间在计算机中的一种表示,它的目的是为了解决空间规模问题,或者是通过空间规模问题从而间接地解决时间规模问题。我们知道,随着输入的数据量越来越大,在有限的内存里,不能把这些数据完全的存下来,这就对数据存储结构和设计存储的算法提出了更高的要求。
本文将介绍几种存储结构,分别为链式结构、树形结构、图结构以及矩阵结构。
第一节 链式存储结构
所谓链式存储结构,一般就是用一个头指针指向链表的第一个节点,如果你要增加新的存储元素时,只需在已有节点的后面插入新结点即可。
链表通常有单链表、双链表、循环链表。在这,我只介绍单链表,双链表和循环链表只是单链表的拓展罢了。下图就是一个简单的单链表图示。

单链表的类型描述如下代码:
- typedef char DataType;
- typedef struct node{
- DataType data;
- struct node *next;
- }ListNode;
- typedef ListNode *LinkList;
- ListNode *p;
- LinkList head;
- 附注:
- ① LinkList和ListNode *是不同名字的同一个指针类型(命名的不同是为了概念上更明确)
- ② LinkList类型的指针变量head表示它是单链表的头指针
- ③ ListNode *类型的指针变量p表示它是指向某一节点的指针
下面我们来看单链表的操作:创建节点、增加节点、删除节点、查询、修改。
1.创建节点:声明一个节点并为其申请一段内存空间,此节点有数据域和指针域。
- node = (struct List *)malloc(sizeof(struct List));
2.增加节点:插入节点,分为头插入、尾插入和非头尾插入。
①. 在表头插入节点,
如图
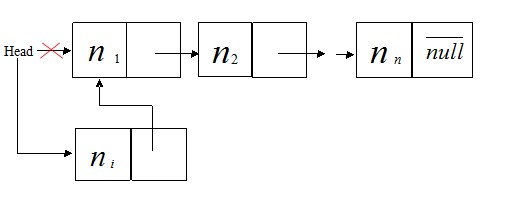
插入头节点的代码如下:
- if(p == head)
- {
- struct list *s = NULL;
- s = (struct list *)malloc(sizeof(struct list));
- s->DataNumber = data;
-
-
- s->next = p;
- head = s;
- }
②. 在表尾插入节点,
如图
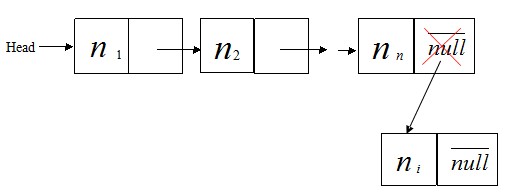
插入尾节点的代码如下:
- if(p->next == NULL)
- {
- struct list *s = NULL;
- s = (struct list *)malloc(sizeof(struct list));
- s->DataNumber = data;
-
-
- p->next = s;
- s->next = NULL;
- }
③. 在表中插入非头尾节点,
如图
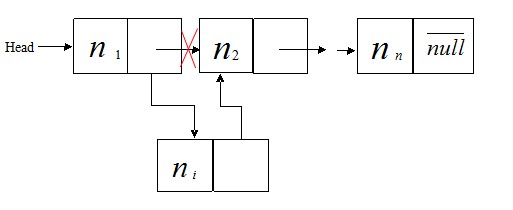
插入非头尾节点的代码如下:
- struct list *s = NULL;
- s = (struct list *)malloc(sizeof(struct list));
- s->DataNumber = data;
-
-
- s->next = p;
- q->next = s;
3.删除节点:分为删除头结点,删除尾节点,删除头尾节点。
①. 删除表头结点,
如图
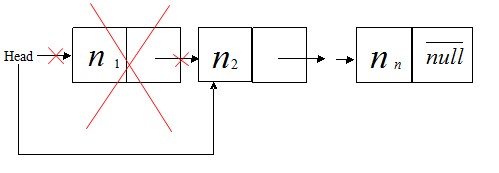
删除头结点的代码如下:
- if(p == head)
- {
- head = p->next;
- }
②. 删除表尾节点,如图
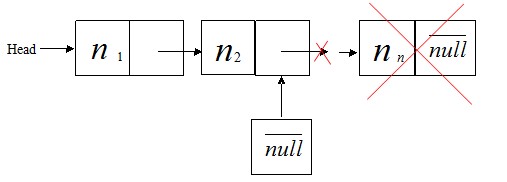
附注说明:上图中删完尾节点之后,新链表的尾节点下标应为n-1。不过由于作图时只做了尾节点,故用图中的n2节点代替。
删除尾节点的代码如下:
- if(p->next == NULL)
- {
- q->next = NULL;
- }
③. 删除非头尾节点,如图

删除非头尾节点的代码如下:
4.查询节点:在链表中找到你想要找的那个节点。此操作是根据数据域的内容来完成的。查询只能从表头开始,当要找的节点的数据域内容与当前不相符时,只需让当前节点指向下一结点即可,如此这样,直到找到那个节点。
附注:此操作就不在这用图和代码说明了。
5.修改节点:修改某个节点数据域的内容。首先查询到这个节点,然后对这个节点数据域的内容进行修改。
附注:同上
ok,链表的几种操作介绍完了,接下来我们来总结一下链表的几个特点。
链式存储结构的特点:
1.易插入,易删除。不用移动节点,只需改变节点中指针的指向。
2.查询速度慢:每进行一次查询,都要从表头开始,速度慢,效率低。
扩展阅读
链表:http://public.whut.edu.cn/comptsci/web/data/512.htm
第二节 树形存储结构
所谓树形存储结构,就是数据元素与元素之间存在着一对多关系的数据结构。在树形存储结构中,树的根节点没有前驱结点,其余的每个节点有且只有一个前驱结点,除叶子结点没有后续节点外,其他节点的后续节点可以有一个或者多个。
如下图就是一棵简单的树形结构:
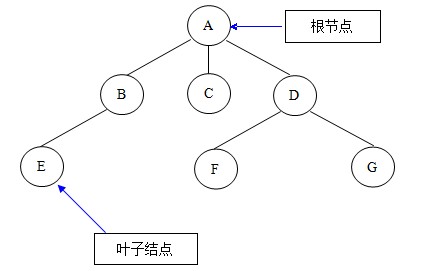
说到树形结构,我们最先想到的就是二叉树。我们常常利用二叉树这种结构来解决一些算法方面的问题,比如堆排序、二分检索等。所以在树形结构这节我只重点详解二叉树结构。那么二叉树到底是怎样的呢?如下图就是一颗简单的二叉树:
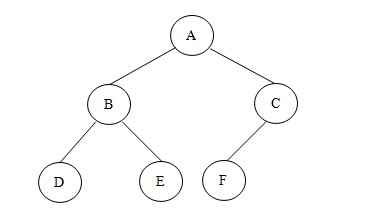
附注:有关树的概念以及一些性质在此不做解释,有意者请到百科一览。
二叉树的类型描述如下:
- typedef struct tree
- {
- char data;
- struct tree * lchild, * rchild;
- }tree;
二叉树的操作:创建节二叉树,创建节点,遍历二叉树,求二叉树的深度。
1.创建二叉树:声明一棵树并为其申请存储空间。
- struct tree * T = NULL;
- T = (struct tree *)malloc(sizeof(struct tree));
2.创建节点:除根节点之外,二叉树的节点有左右节点之分。

创建节点的代码如下:
- struct tree * createTree()
- {
- char NodeData;
- scanf(" %c", &NodeData);
- if(NodeData == '#')
- return NULL;
- else
- {
- struct tree * T = NULL;
- T = (struct tree *)malloc(sizeof(struct tree));
- T->data = NodeData;
- T->lchild = createTree();
- T->rchild = createTree();
- return T;
- }
- }
3.遍历二叉树:分为先序遍历、中序遍历、后续遍历。
①.先序遍历:若二叉树非空,则依次执行如下操作:
(1) 访问根结点;
(2) 遍历左子树;
(3) 遍历右子树。
如图:
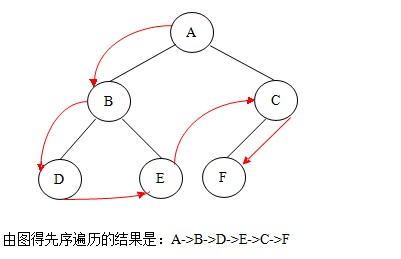
先序遍历的代码如下:
- void PreTravser(struct tree * T)
- {
- if(T == NULL)
- return;
- else
- {
- printf("%c",T->data);
- PreTravser(T->lchild);
- PreTravser(T->rchild);
- }
- }
②.中序遍历:若二叉树非空,则依次执行如下操作:
(1)遍历左子树;
(2)访问根结点;
(3)遍历右子树。
如图:
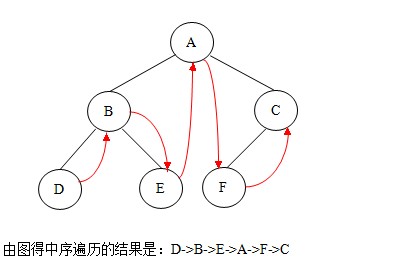
中序遍历的代码如下:
- void MidTravser(struct tree * T)
- {
- if(!T)
- {
- return;
- }
- else
- {
- MidTravser(T->lchild);
- printf("%c",T->data);
- MidTravser(T->rchild);
- }
- }
③.后续遍历:若二叉树非空,则依次执行如下操作:
(1)遍历左子树;
(2)遍历右子树;
(3)访问根结点。
如图:

后续遍历的代码如下:
- void PostTravser(struct tree * T)
- {
- if(!T)
- return;
- else
- {
- PostTravser(T->lchild);
- PostTravser(T->rchild);
- printf("%c->",T->data);
- }
- }
4.求二叉树的深度:树中所有结点层次的最大值,也称高度。
二叉树的深度表示如下图:
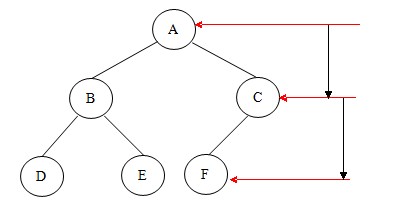
求二叉树深度的代码如下:
- int treeDeepth(struct tree * T)
- {
- int i, j;
- if(!T)
- return 0;
- else
- {
- if(T->lchild)
- i = treeDeepth(T->lchild);
- else
- i = 0;
-
- if(T->rchild)
- j = treeDeepth(T->rchild);
- else
- j = 0;
- }
- return i > j? i+1:j+1;
- }
好了,二叉树的几种操作介绍完了。
拓展阅读
二叉树:http://student.zjzk.cn/course_ware/data_structure/web/DOWNLOAD/%CA%FD%BE%DD%BD%E1%B9%B9%D3%EB%CB%E3%B7%A82.htm
赫夫曼编码:http://blog.csdn.net/fengchaokobe/article/details/6969217
第三节 图型存储结构
所谓图形结构,就是数据元素与元素之间的关系是任意的,任意两个元素之间均可相关,即每个节点可能有多个前驱结点和多个后继结点,因此图形结构的存储一般是采用链接的方式。图分为有向图和无向图两种结构,如下图
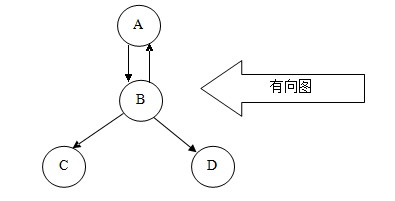
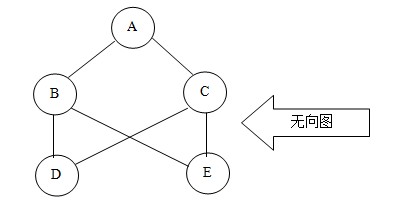
通过图,我们可以判断两个点之间是不是具有连通性;通过图,我们还可以计算两个点之间的最小距离是多少;通过图,我们还可以根据不同的要求,寻找不同的合适路径。
1.图的结构有好几种,在实际应用中需根据具体的情况选择合适的结点结构和表结构。常用的有数组结构、邻接表。
①.数组结构
数组结构的类型描述如下:
- typedef char VertexType;
- typedef int EdgeType;
- #define maxvex 100 /***顶点的最大个数***/
-
- typedef struct
- {
- VertexType vexs[maxvex];
- EdgeType arc[maxvex][maxvex];
- }Mgraph;
附注:当前图为无向图时,图中某两个顶点VA和VB构成一条边时,其权值可表示为EdgeType arc[VA][VB];当前图为有向图时,图中某两个顶点VA和VB构成一条边时,并且是由VA指向VB,其权值可表示为EdgeType arc[VA][VB],如果是由VB指向VA,其权值可表示为EdgeType arc[VB][VA]。
②.邻接表
邻接表的类型描述如下:
- typedef char VertexType;
- typedef int EdgeType;
-
- typedef struct EdgeNode
- {
- int adjvex;
- EdgeType weight;
- struct EdgeNode *next;
- }EdgeNode;
-
- typedef struct VertexNode
- {
- VertexType data;
- EdgeNode * firstedge;
- }VertexNode,AdjList[MAXVEX];
-
- typedef struct
- {
- AdjList adjList;
- int numVertexes,numEdges;
- }GraphAdjList;
2.图的遍历:从图中的某一节点出发访问图中的其余节点,且使每一节点仅被访问一次。图的遍历算法是求解图的连通性问题、拓扑排序和求路径等算法的基础。图的遍历分为深度优先遍历和广度优先遍历,且它们对无向图和有向图均适用。
①. 深度优先遍历
定义说明:假设给定图G的初态是所有顶点均未曾访问过。在G中任选一顶点V为初始出发点,则深度优先遍历可定义如下:首先访问出发点V,并将其标记为已访问过;然后依次从V出发搜索v的每个邻接点W。若W未曾访问过,则以W为新的出发点继续进行深度优先遍历,直至图中所有和源点V有路径相通的顶点(亦称为从源点可达的顶点)均已被访问为止。若此时图中仍有未访问的顶点,则另选一个尚未访问的顶点作为新的源点重复上述过程,直至图中所有顶点均已被访问为止。
深度遍历过程如下图:
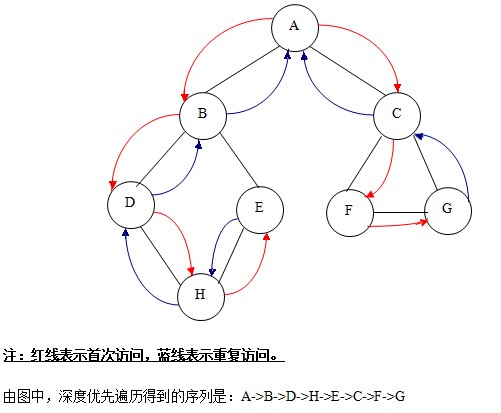
②. 广度优先遍历
定义说明:假设从图中某顶点V出发,在访问了V之后一次访问V的各个未曾访问过的邻接点,然后分别从这些邻接点出发依次访问它们的邻接点,并使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问,直至图中所有已被访问的顶点的邻接点都被访问到。若此时图中还有顶点未被访问,则另选图中一个未曾被访问的顶点作为起始点,重复上述过程,直至图中所有顶点都被访问到为止。换句话说,广度优先遍历图的过程是以V为起点,由近至远,依次访问和V有路径相同且路径长度为1,2,...的顶点。
广度遍历过程如下图:
作者:csh624366188 发表于2012-4-9 22:54:15
原文链接