第14章 通用性能测试结果分析 截至第13章,小白已经完成了LoadRunner测试脚本的编写、场景的建立,并成功地执行测试及分析了整个测试结果、产生了测试报告。本书对于LoadRunner这一强大的工具也已经基本介绍完毕了。但是,在实际工作中,性能测试工程师可能并不一定采用LoadRunner,而是使用其他的工具甚至自行编程来取得相关的性能测试数据。那么,有没有通用的一些分析性能测试数据的经验呢?
本章的内容就能够回答上述这个问题。如果说第12章中LoadRunner所提供的性能图表与测试报告是汽车中的自动挡,那么本章就是汽车中的手动挡。作为一名性能测试工程师,必须能够脱离工具软件的束缚,直接从原始的数据中得到正确的结论,才称得上合格。
初学者都知道,性能测试得到的数据,如果不进行分析,得到的结果是没有多大价值的。而在分析性能测试结果的过程中,往往需要用到简单的数学知识来进行评 估、敏锐的观察能力来发现隐藏在数据中的性能问题;另外,出色的文档编写能力和图表制作能力则有利于将测试工程师了解到的事实有效地传递到相关人员的印象 当中。其中,工作中最重要、也可能是最耗费时间与精力、同时又是收获最大的部分就是发现性能问题。
本章将依据以上这几种能力分为3节来 介绍:第1节介绍判别测试数据是否可靠的要点,其中包含了一些简单的统计学知识。第2节通过几个范例来讲解发现性能的技巧与经验。第3节将列出编写性能测 试报告的注意事项与要点,同时,对Office Excel软件中的画图功能也进行了较详细的说明。
14.1 性能测试结果的可靠性
性能测试的结果往往由大量数据组成,在我们拿到这些数据之后,首先要判断这些数据是否可靠。一些简单的统计学指标可以使我们很快地从数据中获得对于性能 的基本印象。因此,本节先借助一些数学知识,让我们能够使用统计学上的简单指标对结果进行简单归纳;之后,再介绍判断性能测试结果可靠性的几条经验规则。
本节中将要介绍、同时也是测试结果分析中较为常用的数学指标有如下几种:
平均值(Mean Value);
中值(Median Value);
正常值(Normal Value);
标准偏差(Standard Deviation);
正态分布(Normal Distribution);
一致分布(Uniform Distribution);
置信区间(Confidence Intervals)。
为了理解方便,我们就使用小白获得的一手响应时间作为例子,学习如上数学指标的具体含义,从而获得总体性能的更直观印象。
14.1.1 原始数据
小白手中有关公司网站响应时间的数据一共分为4组,分别代表了客户端不同操作端系统、不同浏览器下访问首页的数据,分别如表14-1、表14-2、表14-3、表14-4所示。
表14-1 Windows XP下通过IE 6访问公司网站的响应时间数据(秒)
表14-2 Windows XP下通过Firefox 3访问公司网站的响应时间数据(秒)
表14-3 Windows Vista下通过IE 7访问公司网站的响应时间数据(秒)
表14-4 Windows Vista下通过Firefox 3访问公司网站的响应时间数据(秒)
从以上数据来初步观察,响应时间长短参差不齐,表面上看分布也没有什么规律。
14.1.2 平均值 所谓平均值(Mean Value),就是把所有数值都相加,然后除以这些数值的个数。平均值也叫做算术平均数。平均值对于某类数据是非常有用的,比如考试成绩,年龄数据等。但是,在14.1.1所举出的数据来说,平均值并不能说明问题,甚至会隐藏可能的性能问题。
【实战演练:平均值的计算】
比如,在14.1.1的4个表格当中,就平均值来看,表现最好的应该是表14-2。这是因为,表14-1、表14-2、表14-3、表14-4的平均值依次为:
(5+6+4+8+13+10+4+4+5+7+8+10)/12 = 7;
(1+12+5+7+8+2+2+4+12+13+1+1)/12 = 5.67;
(6+6+6+8+12+12+14+4+8+6+6+6+6)/12 = 8.33;
(6+6+7+8+8+7+6+6+9+6+11+9)/12 = 7.41。
以上数值的单位均为秒。从结果中可以发现,表14-2响应时间的平均值确实是最短的。但是,需要注意的是,表14-2中的数据"两极分化"比较 严重,既有很短的1秒,也有很长的13秒,而在平均值5.67秒附近的数值却很少。这样的情况就可能暴露出网站性能的某些问题,或者是数据采集中的不科学 性。
读者在实际工作中得到测试结果的时候,不能单单记录数值,同时还要思考如下等问题:
响应时间很短是否由于缓存的缘故?
响应时间很长是否是Web应用代码的问题?
不同浏览器的响应时间有什么规律?
在测试过程中,对得到的数据多问几个为什么,有助于提高测试的准确性。
14.1.3 中值
中值的引入能够发现部分14.1.2节中表14-2中的数据问题。
【中值是什么】
所谓中值(Median Value),就是将数据从小到大排列起来,中间那个数的数值。
将中值的定义应用于实际,比如对于表14-1来说,其数据从小到大的排列依次为:
| 4 4 4 5 5 6 7 8 8 10 10 13 |
如果这一系列数据的个数为单数,中值就是中间那个数的值。如果类似表14-1的情况,数据个数是12,为偶数,则中值一般认为是最中间两个数值(这里是第6个和第7个)的平均值,即(6+7)/2=6.5。
经过计算,表14-1、表14-2、表14-3、表14-4的中值分别为6.5、4.5、6和7。
【中值与平均值的关系】
中值虽然不等同于平均值,但若中值与平均值越接近,则说明数据分布的越均匀。
14.1.4 正常值
正常值(Normal Value)并不一定意味着它的值是正常的。所谓正常值,是指在数据结果中出现频率最多的那个值,通俗地说,就是在它们中间最容易碰到的数值。表 14-1、表14-2、表14-3和表14-4中的正常值分别为1、4、6、6秒,可见,正常值与平均值、中值可能会有很大差别。
【实战演练:正常值的判断】
设想这样一个场景:小白所测试的Web应用有某部分代码出现了问题,导致数据库连接经常超时,测得的响应时间序列为20、25、30、26、 26、27、26等,在这样的数值当中,26是正常值,但它绝不是网站正常时应该具备的响应时间,因此,它又是"不正常"的。实际工作中这样的情况并不鲜 见,读者在处理数据时一定要首先保证数据的有效性。
性能测试中正常值的意义在于发现当前配置下,多数情况采集到的数值是什么。
14.1.5 标准偏差
标准偏差提供了比中值更准确的方法,来确定数值是否"聚集"在平均值附近。标准偏差(Standard Deviation)是一种度量数据分布分散程度的标准,它可以用来衡量具体数据值偏离平均值(算术平均值)的程度。标准偏差越小,这些值偏离平均值就越 少,数据就越可信。反之,数值偏离平均值越大,数据就越不可信。
【实战演练:Excel计算标准偏差】
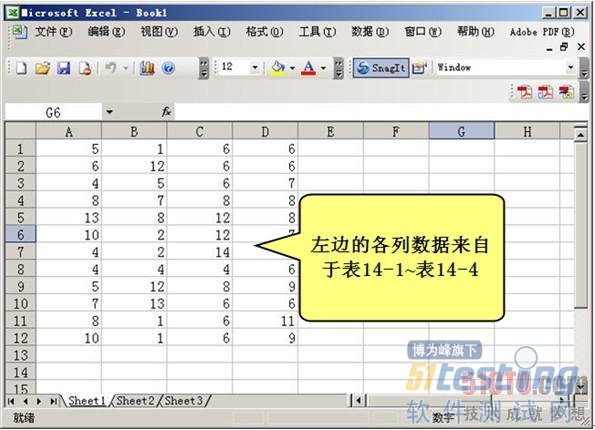
标准偏差的计算不是本书讲解的内容,我们只需理解它的含义会用工具计算就可以了。常见的计算标准偏差的工具软件就是微软的Excel。如图14-1中新建了一个工作表,其中有4列,每一列分别包含表14-1到表14-4的测试数据。
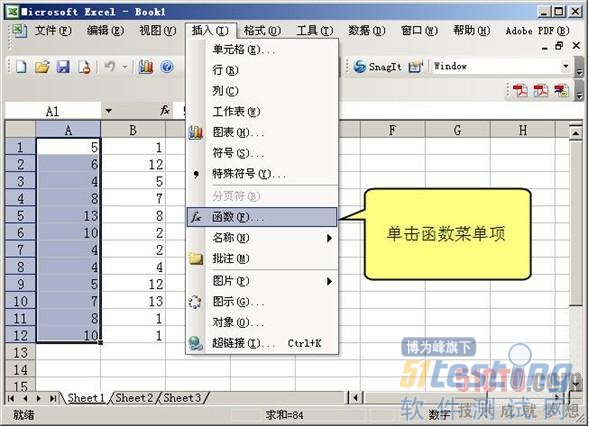
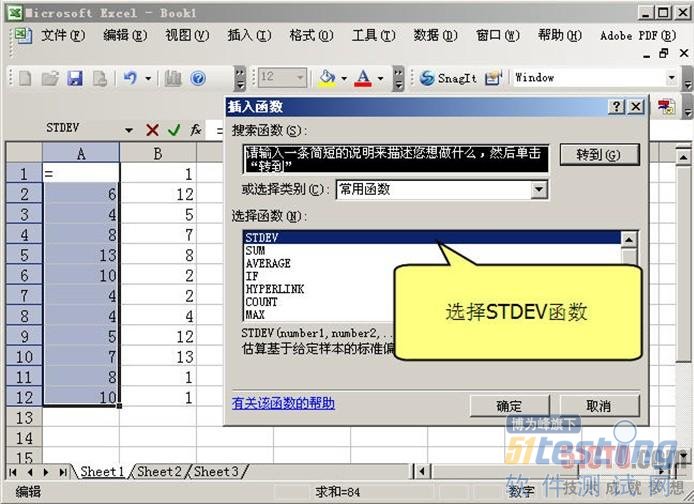
下面举例计算前面表14-1中数据(已经录入在图14-1工作表的A列之中)的标准偏差。首先,单击工作表中的A列,然后选择"插入"|"函 数"命令,如图14-2所示。之后Excel将弹出函数选择对话框,在其中找到计算标准偏差的STDEV函数即可,如图14-3所示。
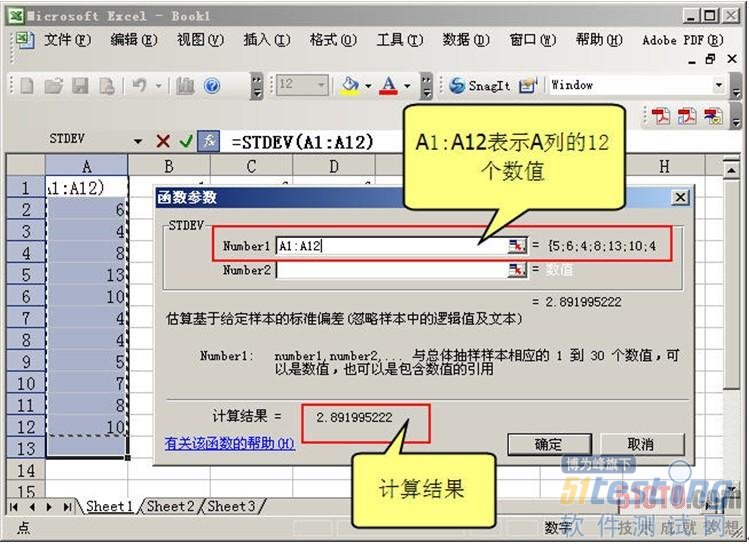
计算标准偏差需要输入一系列的数值,这也是在图14-2中要首先选中A列或其他列的原因。在图14-3中单击"确 定"按钮之后,Excel将弹出函数参数对话框。如果其中的Number1文本框内没有数值,读者可以填入文字A1:A12,以表示A列的所有12个数值 作为计算的输入,依次类推。确认输入数据无误后,单击"确定"按钮,计算结果将立即显示在当前的对话框内,如图14-4所示。
通过前文这样的方法,依次可以得到从表14-1到表14-4所包含测试数据的标准偏差,分别为:2.8919、4.6384、3.1285和1.6213。根据前面所介绍的"标准偏差数值越小数据越值得信赖"原则,很显然,表14-4所包含的数据更具有可信度。
对测试结果进行标准偏差的计算,有利于从中发现更具可信度的度量数值。
14.1.6 正态分布 正态分布(Normal Distribution)也叫做钟形分布,这个名字是因为正态分布的数值在图形上类似一口钟而得来。它的含义就是一系列的数值当中,靠近中值附近的数值 数量最多,而偏离中值的数值数量则不断减少。人类社会的很多行为都符合正态分布的特点,我们常说的"随大流"也可以说是一个体现吧:大多数人的行为都是非 常类似的。
一个典型的正态分布图如图14-5所示。在性能测试产生的数据中,足够大量的响应时间具有正态分布的特点。
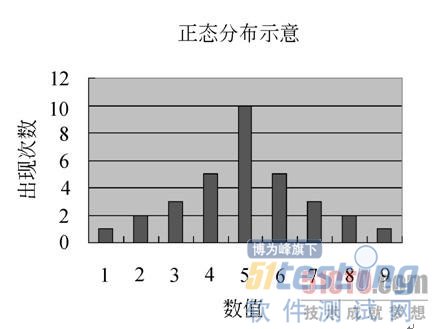
图14-5 正态分布(钟形分布)示意图
【正态分布与标准偏差的关系】
正态分布与标准偏差有很大的关系,一般来说,标准偏差越小,数值越接近正态分布。因为正态分布存在非常普遍,所以才拥有了Normal这样的名字。
14.1.7 一致分布
一致分布(Uniform Distribution)顾名思义是指测试所取得的数据值相差很小,简单粗略地看,在图中会表现为波动很小的近似直线,如下面的情况。
【实战演练】
小白所在的公司每周要发送一个邮件列表给注册用户,该列表的内容实际上是一个由市场、销售部门HTML页面。由于发 送程序运行在数据库服务器上(因为每周一次,也是周日晚间发送,所以暂时没有必要使用专门的服务器来完成),为了不显著影响整体性能,需要对HTML页面 的大小进行限制。为此,小白记录了若干次的文件大小,如表14-5所示。
表14-5 每周邮件列表文件大小
| 日 期 | 文 件 大 小 |
| 2008年9月6日 | 47KB |
| 2008年9月13日 | 48KB |
| 2008年9月20日 | 47KB |
| 2008年9月27日 | 48KB |
如果在Excel中对表14-5所列出的数据画成图,就可以看成是一致分布,如图14-6所示。
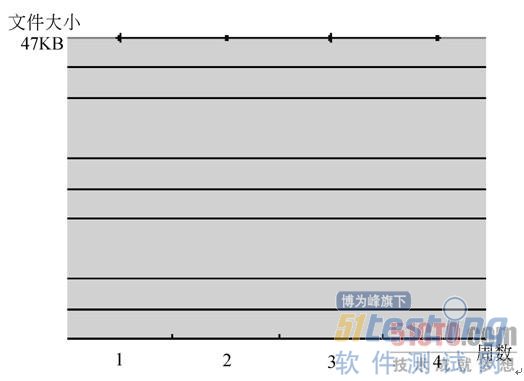
图14-6 邮件列表内容文件大小呈一致分布
每次邮件列表大小基本一致,是因为市场、销售部充分利用了文件大小的上限,尽量争取在有限的大小之内,放入更多的宣传内容。当然,在实际工作情形中,不一定每次都会出现这样的情况。
如果在性能测试中出现了一致分布的数据,测试工程师需要找出原因,一般来说,这样的数据反而是值得怀疑的。比如响应时间,如果用户的响应时间惊人的一致,则要考虑是否有部分用户因为某些原因根本无法访问网站等原因。
14.1.8 置信度与置信区间
在性能测试领域,置信度指的是测试结果与真实结果之间的差别。由于具体的测试结果是由用户使用Web应用方式的估计模型和性能测试方法决定的,因此也可以认为置信度反映了网站人员与最终用户在使用该Web应用上的相似度。
【置信度举例】
举例来说,小白所在公司的人都认为用户将更喜欢网站的A栏目,因此在资源有限的情况下,测试部对该栏目的功能进行了重点性能测试,并进行了优 化,获得了不错的结果;但实际网站上线后,用户却更喜欢另外某个栏目,经常使用的功能也与事先预想的不同。这就会导致性能测试结果与实际性能测量值有所误 差。这种误差大小的程度就是置信度。当然,这样的理解在数理统计方面并不严格,但对于性能测试工程师在工作中的使用已经可以了。
置信度越高,置信区间(Confidence Interval)也就越接近真实值的范围。置信区间是指在某一置信度水平下,性能测试结果与Web应用上线后实际运行结果间的误差范围。要知道在Web 应用上线前,没有谁能准确地预计用户行为,因此有必要在进行性能测试时预估一个置信度,再根据结果得到置信区间。
【置信区间的实际使用】
假设公司对网站响应时间设置的合理值为10秒以下,置信度估计为80%。小白在对网站使用LoadRunner进行并发测试后,发现:由于使用 页面功能不同,最差的情况一次并发50个用户就可能令第51个用户响应时间超标;而最好的情况则是一次并发300个用户才能令响应时间超标。那么,在测试 结果报告中,小白应当这样进行陈述:根据80%置信度,在一般工作负荷下,并发数为50×80%到300×80%,即40~240个用户,都不会引起响应 时间超标。这里的40~240就是置信区间。
综上所述,置信度也可以理解为一种形式的安全系数。
14.1.9 数据可靠性判断的规则
前面讲述了一些统计学的知识,实际目的都是为了使得我们的性能测试报告能够更接近于真实,这样才能发挥最大的作用。因此,在测试结果出来之后,并不要立刻发送测试报告,而是要先判断取得的测试数据是否可靠,这样的能力对于性能测试工程师来说是非常必要的。
数据可靠性有如下几条经验规则:
(1)如果有超过20%的测试数据明显与其他数据有很大差别,则应该先检查测试过程中是否出现问题。这样的情况是经常发生的:小白使用很多台测 试机器在下班后运行自动访问公司网站的脚本程序,从而记录响应时间等数据。但由于其中某些机器设置了Windows系统默认凌晨3点发生的自动更新,可能 会强迫重启电脑,从而导致测试中断,在重启过程中取得的响应时间数据当然是不可靠的。
(2)如果进行了多次相同目的的性能测试,如果某一次测试绝大多数结果比其他几次测试中最大的结果都要大,或者比它们当中最小的结果都要小,那 么应该考虑这次测试结果的有效性问题。这一点是很好理解的。至于绝大多数的比例设定为多少,可以根据实际情况来定,一般至少在75%以上。
根据以上这两条基本原则,再结合具体被测试软件的实际情况,就可以判断出哪些数据是可靠的,哪些数据是不可靠的。有了可靠的数据,才能编写出可靠的测试报告,这是最重要的一点。
在14.2节,本书将简要介绍性能测试结果的分析方法,这是性能测试报告的关键。
(未完待续)
相关链接:
捉虫记--大容量Web应用性能测试与LoadRunner实战(连载一)
捉虫记--大容量Web应用性能测试与LoadRunner实战(连载二)
捉虫记--大容量Web应用性能测试与LoadRunner实战(连载三)
捉虫记--大容量Web应用性能测试与LoadRunner实战(连载四)
捉虫记--大容量Web应用性能测试与LoadRunner实战(连载五)
捉虫记--大容量Web应用性能测试与LoadRunner实战(连载六)