在介绍空间索引之前,先谈谈什么叫“索引“。对一个数据集做”索引“,是为了提高对这个数据集检索的效率。书的”目录“就是这本书内容的”索引“,当我们拿到一本新书,想查看感兴趣内容的时候,我们会先查看目录,确定感兴趣的内容会在哪些页里,直接翻到那些页,就OK了,而不是从第一章节开始翻,一个字一个字地找我们感兴趣的内容,直到找到为止,这种检索内容的效率也太低了,如果一本书没有目录,可以想象有多么不方便…可见书的目录有多重要,索引有多重要啊!
现在大家对索引有了感性认识,那什么是“空间索引“呢?”空间索引“也是”索引“,是对空间图形集合做的一个”目录“,提高在这个图形集合中查找某个图形对象的效率。比如说,我们在一个地图图层上进行矩形选择,确定这个图层上哪些图元被这个矩形所完全包含呢,在没有”空间索引“的情况下,我们会把这个图层上的所有图元,一一拿来与这个矩形进行几何上的包含判断,以确定到底哪些图元被完全包含在这个矩形内。您是不是觉得这样做很合理呢?其实不然,我们先看一个网格索引的例子:
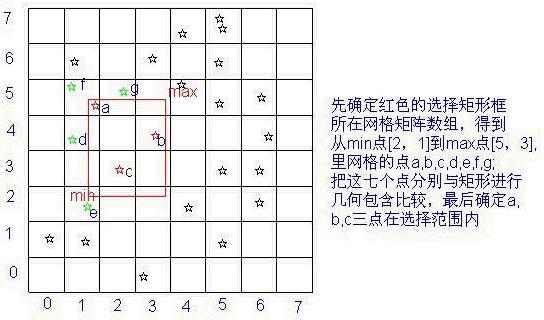
我们对这个点图层作了网格索引,判断哪些点在这个矩形选择框内,是不需要把这个图层里所有的点都要与矩形进行几何包含运算的,只对a,b,c,d,e,f,g这七个点做了运算。可以推想一下,如果一个点图层有十万个点,不建立空间索引,任何地图操作都将对整个图层的所有图元遍历一次,也就是要For循环10万次;建立索引将使得For循环的次数下降很多很多,效率自然提高很多!
呵呵…想必大家都知道空间索引的好处了,也不知不觉向大家介绍了点图层的网格索引,还有哪些常用的空间索引呢?这些空间索引又该如何实现呢?带着这样的问题,下面介绍几种常用的空间索引。
网格索引
网格索引就是在一个地图图层上,按每个小网格宽△w,高△h打上均匀的格网,计算每个图元所占据的网格或者所经过的网格单元集合,
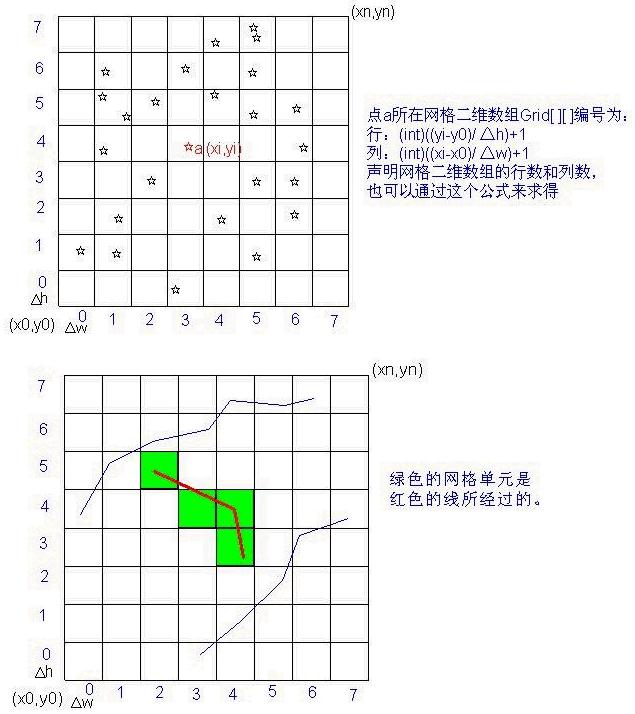
在这些网格单元中,记录下图元对象的地址或者引用,比如:声明一个对象二维数组 List grid[m][n]; m代表网格的行数,n代表网格的列数,每个数组元素为一个“集合对象”,用于存储这个网格单元所关联的所有图元的地址或引用,这样网格索引就建立好了。下一步,我们该怎么用这个网格索引呢?所有的图形显示和操作都可以借助于“空间索引”来提高效率。举几个例子来说明“空间索引“的使用:
一、放大开窗显示,正如上一节介绍的,当我们在地图上画一个矩形想放大地图的时候,首先得确定放大后的地图在屏幕上需要显示哪些图元?所以,我们需要判断这个地图中有哪些图元全部或者部分落在这个矩形中。判断步骤:
1,确定所画矩形左上角和右下角所在的网格数组元素;即可得到这个矩形所关联覆盖的所有网格集合;
2,遍历这个网格集合中的元素,取到每个网格元素List中所记录的图元;
3,画出这些图元即可。(当然整个过程涉及到两点:1,屏幕坐标和地图坐标的互相变换;2,窗口裁减,也可以不裁减)
二、包含判断,给出一个点point和一个多边形polygon,判断点是否在面内,首先判断这个点所在的网格,是否同时关联这个polygon,如果不是,表明点不在面内,如果是,可以下一步的精确解析几何判断,或者精度允许的情况下,即判断polygon是包含point的。
另外,Google Map应该也是采用地理网格的方式,对地图图象进行索引的,可见一斑,网格索引在图形显示,选择,拓扑判断上的广泛应用。但同时也存在很严重的缺陷:当被索引的图元对象是线,或者多边形的时候,存在索引的冗余,即一个线或者多边形的引用在多个网格中都有记录。随着冗余量的增大,效率明显下降。所以,很多学者提出了各种方法来改进网格索引,这个将在下面的章节中介绍。而点图元非常适合网格索引,不存在冗余问题。
四叉树索引(Quadtree)
类似于前面介绍的网格索引,也是对地理空间进行网格划分,对地理空间递归进行四分来构建四叉树,本文将在普通四叉树的基础上,介绍一种改进的四叉树索引结构。首先,先介绍一个GIS(Geographic Information System)或者计算机图形学上非常重要的概念——最小外包矩形(MBR-Minimum Bounding Rectangle):
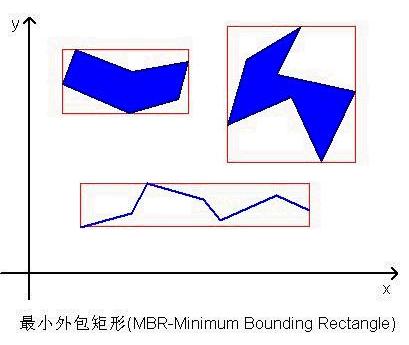
最小外包矩形MBR就是包围图元,且平行于X,Y轴的最小外接矩形。MBR到底有什么用处呢,为什么要引入这个概念呢?因为,图元的形状是不规则的,而MBR是平行于X,Y轴的规则图形,设想一下,如果所有的图元都是平行于X,Y轴的矩形,那针对这样的矩形进行几何上的任何判断,是不是要简单很多呢?不管我们人自己写公式算法或者编写程序运行,是不是都要比原本复杂的图形几何运算要简洁很多呢?答案很显然。
然后,我们再介绍一下GIS空间操作的步骤(这个步骤,在前面忘记向大家说明了,在这里补充一下)
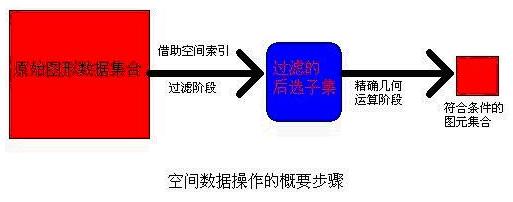
可见,过滤阶段,通过空间索引可以排除掉一些明显不符合条件的图元,得到后选集合,然后对后选图元集合进行精确几何运算,得到最终结果。大家可能会有这样的疑问,这样有必要吗?是不是反而把问题复杂化了?合适的空间索引只会提高计算机的效率,没有空间索引,我们无疑要对集合中的每个图元进行精确几何运算,而这样的运算是复杂的,是非常占用CPU的,所以需要空间索引,采取少量的内存和简单的CUP运算,来尽量减少那种高耗CUP的精确运算的次数,这样做是完全值得的。至于精确的几何运算到底复杂在哪里,该如何进行精确的几何运算,将在下面的章节中详细描述,这里主要介绍过滤阶段的空间索引。
现在,让我们来具体了解一下“四叉树索引”。
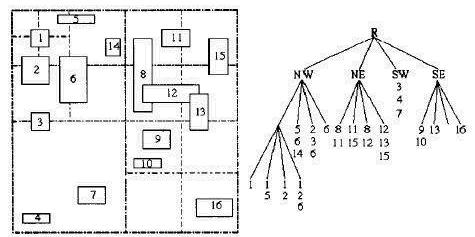
四叉树索引就是递归地对地理空间进行四分,直到自行设定的终止条件(比如每个节点关联图元的个数不超过3个,超过3个,就再四分),最终形成一颗有层次的四叉树。图中有数字标识的矩形是每个图元的MBR,每个叶子节点存储了本区域所关联的图元标识列表和本区域地理范围,非叶子节点仅存储了区域的地理范围。大家可以发现,同样存在一个图元标识被多个区域所关联,相应地存储在多个叶子节点上,比如“6“所代表的图元,分别存储在四个分枝上。这样,就存在索引的冗余,与网格索引存在同样的弊端。下面我们介绍一种改进的四叉树索引,或者说是分层的网格索引。
改进的四叉树索引,就是为了避免这种空间索引的冗余,基本改进思路是:让每个图元的MBR被一个最小区域完全包含。
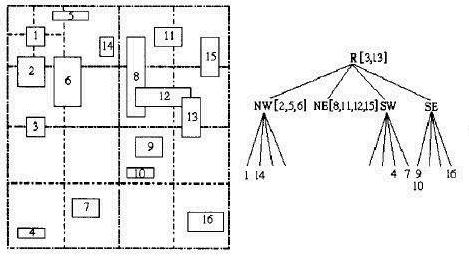
可以看出,3和13分别都跨越了两个区域,要被一个最小区域完全包含,就只能是根节点所代表的区域,2,5跨越了两个区域,6跨越了四个区域,要被一个最小区域完全包含,就只能是NW区域。怎么判断一个图元被哪个最小区域完全包含呢?从直观上看,递归地对地理空间进行四分,如果图元与一个区域四分的划分线相交,则这个图元就归属于这个区域,或者直到不再划分了,那就属于这个不再划分的区域。呵呵。。。可能有点绕口,看图,结合“最小”“完全包含”这两个字眼,您就明白了。这颗四叉树中,图元的标识不再仅仅存储在叶子节点上,而是每个节点都有可能存储,这样也就避免了索引冗余。同时每个节点存储本节点所在的地理范围。
有了四叉树索引,下面又该如何利用这颗树来帮助检索查找呢?还是矩形选择为例吧!(为什么我总是拿这个例子来说事呢?因为这个例子简单,容易理解,有代表性!)我们在地图上画一个矩形,判断地图上哪些图元落在这个矩形里或者和这个所画矩形相交。方法很多,这里介绍一种简单的检索步骤,如下:
1,首先,从四叉树的根节点开始,把根节点所关联的图元标识都加到一个List里;
2,比较此矩形范围与根节点的四个子节点(或者叫子区域)是否有交集(相交或者包含),如果有,则把相应的区域所关联的图元标识加到List集合中,如果没有,则以下这颗子树都不再考虑。
3,以上过程的递归,直到树的叶子节点终止,返回List。
4,从List集合中根据标识一一取出图元,先判断图元MBR与矩形有无交集,如果有,则进行下面的精确几何判断,如果没有,则不再考虑此图元。(当然,这里只说了一个基本思路,其实还有其他一些不同的方法,比如,结合空间数据磁盘的物理存储会有一些调整)
总结:改进的四叉树索引解决了线,面对象的索引冗余,具有较好的性能,而被大型空间数据库引擎所采用,如ArcSDE,Oracle Spatial等,同时这种结构也适用于空间数据的磁盘索引,配合空间排序聚类,基于分形的Hilbert算法数据组织,将在空间数据格式的定义中发挥重要作用。