线性回归主要用最小二乘法得到直线并进行预测。线性回归真正复杂的地方在于检验,这篇博客主要总结线性回归的检验。
这篇文字涉及到的检验主要包括拟合优度检验,标准差检验,整体自变量显著性检验-F检验,单个系数显著性检验-t检验。
线性回归有一元线性回归和多元线性回归,先说一元的。
拟合优度检验:
对样本回归直线与样本观测值之间拟合程度的检验。用判定系数(可决系数)检验,R2
对于
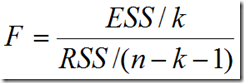
_thumb.png)
_thumb.png)
_thumb.png)
如果Yi=Ŷi 即实际观测值落在样本回归“线”上,则拟合最好。
可认为,“离差”全部来自回归线,而与“残差”无关。
对于所有样本点,则需考虑这些点与样本均值离差的平方和,可以证明:
_thumb.png)
_thumb.png)
Tss = ESS + RSS
Y的观测值围绕其均值的总离差(total variation)可分解为两部分:一部分来自回归线(ESS),另一部分则来自随机势力(RSS)。
在给定样本中,TSS不变,
如果实际观测点离样本回归线越近,则ESS在TSS中占的比重越大,因此
拟合优度:回归平方和ESS/Y的总离差TSS
_thumb.png)
标准差检验:
估计标准误差主要是为了估计总体方差。
所谓估计标准误差是指估计值与观察值的平均差异程度, 用( S) 表示。而 S 2是总体方差( σ 2 ) 的无偏估计量, 即σ^ 2 =S 2 =Σe i的平方 /(n- 2)。该指标的意义是: S 越小表明实际观测点与所拟和的样本回归线的离差程度越小, 即回归线具有较强的代表性; 反之, S 越大表明实际观 测 点 与 所 拟和的样本回归线的离差程度越大, 即回归线的代表性较差。
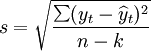
式中:
yt——因变量第t期的观察值;
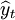 ——因变量第t期的估计值;
——因变量第t期的估计值;
n——观察期的个数;
k——自由度,为变量的个数(包括因变量和自变量)。
判断回归标准差能否通过检验,仍用以下公式:式中:
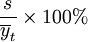
s——回归标准差;
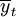 ——因变量观察值的平均值。
——因变量观察值的平均值。
当依此式计算出的值小于15%,说明预测模型通过了回归标准差检验。
一元相关系数检验:
在回归分析预测法中,需要对X、Y之间相关程度作出判断,这就要计算相关系数Y,其公式如下:
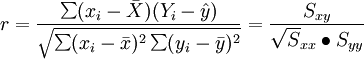
相关系数r的特征有:
①相关系数取值范围为:-1≤r≤1 。
②r与b符合相同。当r>0,称正线性相关,Xi上升,Yi呈线性增加。当r<0,称负线性相关,Xi上升,Yi呈线性减少。
③|r|=0,X与Y无线性相关关系;|r|=1,完全确定的线性相关关系;0<|r|<1,X与Y存在一定的线性相关关系;|r|>0.7,为高度线性相关;0.3<|r|≤0.7,为中度线性相关;|r|≤0.3,为低度线性相关。
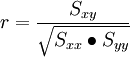
整体自变量显著性检验-F检验 & 单个系数显著性检验-t检验
这两种检验方式在一元中意义是一致的,回归分析中的假设检验包括变量之间的线性关系检验和参数的显著性检验两个内容。前者检验的是解释变量 与被解释变量 能否用一个线性模型来表示,后者检验的是回归模型中的每一个解释变量对被解释变量的影响程度。这两种检验在顺序上是不能颠倒的。
F检验:
根据数从线性回归模型可以看到,如果变量X和Y之间的线性关系是显著的,那么解释变量X的变化必然引起被解释变量Y的显著变化,此时,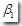 一定不为0。否则被解释变量Y的变化将不依赖于解释变量X的变化,而仅仅依赖于随机误差项。因此,变量之间线性关系的检验问题可以转化为检验
一定不为0。否则被解释变量Y的变化将不依赖于解释变量X的变化,而仅仅依赖于随机误差项。因此,变量之间线性关系的检验问题可以转化为检验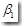 是否为0。由此我们可以给出以下假设:
是否为0。由此我们可以给出以下假设:
原假设 : 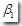 =0 备择假设 :
=0 备择假设 : 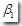 ≠0
≠0
如果原假设成立,那么统计量
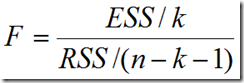
服从自由度为(k , n-k-1)的F分布
如果计算出的F值大于在给定的显著性水平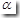 下的临界值
下的临界值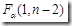 ,则拒绝接受备择假设,说明解释变量对被解释变量有显著影响,即两者线性关系显著。
,则拒绝接受备择假设,说明解释变量对被解释变量有显著影响,即两者线性关系显著。
t检验:
构造出了一个比较复杂的t函数,没理解,参考中,多元线性回归分析预测法和多元线性回归模型拟合优度假设检验都写了具体公式,与F检验类似,也是t值大于临界值时,解释变量有显著影响。
另外,多元线性回归分析预测法也提到了另外两种预测,粗略地看了一下:
多重共线性判别
若某个回归系数的t检验通不过,可能是这个系数相对应的自变量对因变量的影平不显著所致,此时,应从回归模型中剔除这个自变量,重新建立更为简单的回归模型或更换自变量。也可能是自变量之间有共线性所致,此时应设法降低共线性的影响。
当回归模型是根据动态数据建立的,则误差项e也是一个时间序列,若误差序列诸项之间相互独立,则误差序列各项之间没有相关关系,若误差序列之间存在密切的相关关系,则建立的回归模型就不能表述自变量与因变量之间的真实变动关系。D.W检验就是误差序列的自相关检验。检验的方法与一元线性回归相同。
参考:
一元线性回归预测法:
http://wiki.mbalib.com/wiki/%E4%B8%80%E5%85%83%E7%BA%BF%E6%80%A7%E5%9B%9E%E5%BD%92%E9%A2%84%E6%B5%8B%E6%B3%95
[ppt]一元线性回归模型的统计检验: http://wenku.baidu.com/view/ca151ff6f61fb7360b4c65d0.html?from=related
二元线性回归分析预测法:
http://wiki.mbalib.com/wiki/%E4%BA%8C%E5%85%83%E7%BA%BF%E6%80%A7%E5%9B%9E%E5%BD%92%E5%88%86%E6%9E%90%E9%A2%84%E6%B5%8B%E6%B3%95
【doc】第三章 一元线性回归 http://wenku.baidu.com/view/3b3bdbbdc77da26925c5b0fa.html
多元线性回归分析预测法:http://wiki.mbalib.com/wiki/%E5%A4%9A%E5%85%83%E7%BA%BF%E6%80%A7%E5%9B%9E%E5%BD%92%E5%88%86%E6%9E%90%E9%A2%84%E6%B5%8B%E6%B3%95